Menu Close

Prove-that-tan-2A-2tan-A-1-tan-2-A-

Tinku Tara 0 Comments
Pin




Question Number 130221 by bramlexs22 last updated on 23/Jan/21
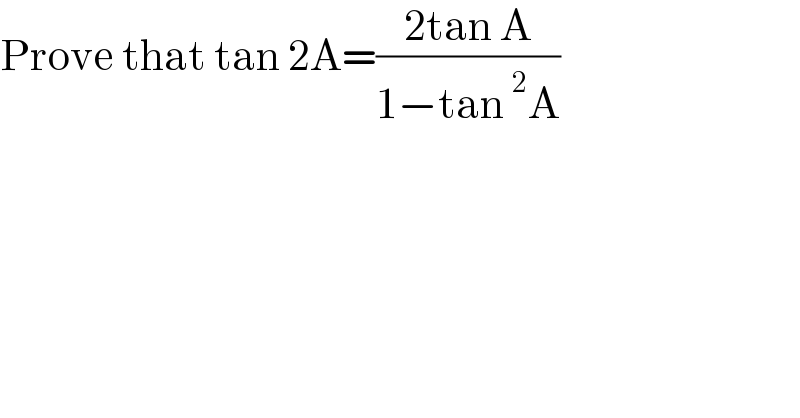
Prove that tan 2A=((2tan A)/(1−tan^2 A))
$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{tan}\:\mathrm{2A}=\frac{\mathrm{2tan}\:\mathrm{A}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \mathrm{A}} \\ $$
Answered by EDWIN88 last updated on 23/Jan/21
by De′Moivre theorem cos 2A+i sin 2A = (cos A+i sin A)^2 = (cos^2 A−sin^2 A)+i (2sin Acos A) ((cos 2A+i sin 2A)/(cos 2A)) = ((cos^2 A−sin^2 A)/(cos 2A)) +i (( 2sin Acos A)/(cos 2A)) 1+ i tan 2A = 1+ i ((2sin Acos A)/(cos^2 A−sin^2 A)) ⇔ tan 2A = (((((2sin Acos A)/(cos^2 A))))/((((cos^2 A−sin^2 A)/(cos^2 A))))) ⇔ tan 2A = ((2tan A)/(1−tan^2 A))
$$\mathrm{by}\:\mathrm{De}'\mathrm{Moivre}\:\mathrm{theorem}\: \\ $$$$\mathrm{cos}\:\mathrm{2A}+{i}\:\mathrm{sin}\:\mathrm{2}{A}\:=\:\left(\mathrm{cos}\:\mathrm{A}+{i}\:\mathrm{sin}\:\mathrm{A}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left(\mathrm{cos}^{\mathrm{2}} \mathrm{A}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{A}\right)+{i}\:\left(\mathrm{2sin}\:\mathrm{Acos}\:\mathrm{A}\right) \\ $$$$\:\frac{\mathrm{cos}\:\mathrm{2A}+{i}\:\mathrm{sin}\:\mathrm{2A}}{\mathrm{cos}\:\mathrm{2A}}\:=\:\frac{\mathrm{cos}\:^{\mathrm{2}} \mathrm{A}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{A}}{\mathrm{cos}\:\mathrm{2A}}\:+{i}\:\frac{\:\mathrm{2sin}\:\mathrm{Acos}\:\mathrm{A}}{\mathrm{cos}\:\mathrm{2A}} \\ $$$$\mathrm{1}+\:{i}\:\mathrm{tan}\:\mathrm{2A}\:=\:\mathrm{1}+\:{i}\:\frac{\mathrm{2sin}\:\mathrm{Acos}\:\mathrm{A}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{A}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{A}} \\ $$$$\Leftrightarrow\:\mathrm{tan}\:\mathrm{2A}\:=\:\frac{\left(\frac{\mathrm{2sin}\:\mathrm{Acos}\:\mathrm{A}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{A}}\right)}{\left(\frac{\mathrm{cos}\:^{\mathrm{2}} \mathrm{A}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{A}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{A}}\right)} \\ $$$$\Leftrightarrow\:\mathrm{tan}\:\mathrm{2A}\:=\:\frac{\mathrm{2tan}\:\mathrm{A}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \mathrm{A}} \\ $$$$ \\ $$
Answered by physicstutes last updated on 23/Jan/21
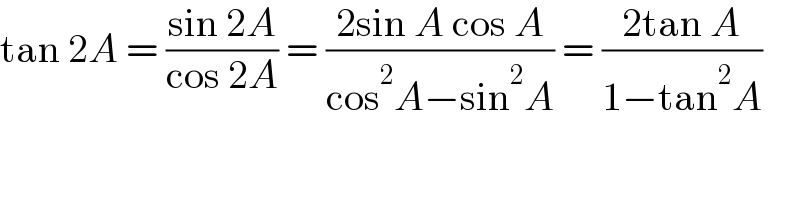
tan 2A = ((sin 2A)/(cos 2A)) = ((2sin A cos A)/(cos^2 A−sin^2 A)) = ((2tan A)/(1−tan^2 A))
$$\mathrm{tan}\:\mathrm{2}{A}\:=\:\frac{\mathrm{sin}\:\mathrm{2}{A}}{\mathrm{cos}\:\mathrm{2}{A}}\:=\:\frac{\mathrm{2sin}\:{A}\:\mathrm{cos}\:{A}}{\mathrm{cos}^{\mathrm{2}} {A}−\mathrm{sin}^{\mathrm{2}} {A}}\:=\:\frac{\mathrm{2tan}\:{A}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} {A}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *