Question Number 81471 by jagoll last updated on 13/Feb/20
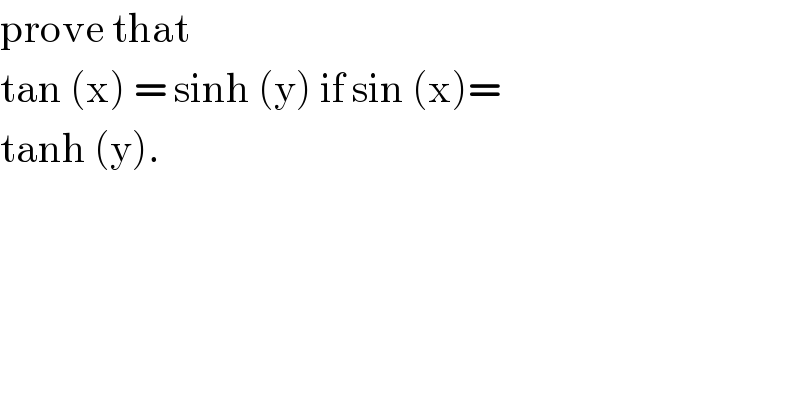
$$\mathrm{prove}\:\mathrm{that}\: \\ $$$$\mathrm{tan}\:\left(\mathrm{x}\right)\:=\:\mathrm{sinh}\:\left(\mathrm{y}\right)\:\mathrm{if}\:\mathrm{sin}\:\left(\mathrm{x}\right)= \\ $$$$\mathrm{tanh}\:\left(\mathrm{y}\right). \\ $$
Commented by john santu last updated on 13/Feb/20

$$\Rightarrow\mathrm{sin}\:\left(\mathrm{x}\right)=\mathrm{tanh}\:\left(\mathrm{y}\right) \\ $$$$\mathrm{squaring}\:\Rightarrow\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{x}\right)=\mathrm{tanh}\:^{\mathrm{2}} \left(\mathrm{h}\right) \\ $$$$\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{x}\right)=\mathrm{1}−\mathrm{tanh}\:^{\mathrm{2}} \left(\mathrm{y}\right) \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{x}\right)=\:\mathrm{sech}\:^{\mathrm{2}} \left(\mathrm{y}\right) \\ $$$$\mathrm{cos}\:\left(\mathrm{x}\right)=\mathrm{sech}\:\left(\mathrm{y}\right) \\ $$$$\mathrm{we}\:\mathrm{get}\:\frac{\mathrm{sin}\:\left(\mathrm{x}\right)}{\mathrm{cos}\:\left(\mathrm{x}\right)}\:=\:\frac{\mathrm{tanh}\:\left(\mathrm{y}\right)}{\mathrm{sech}\:\left(\mathrm{y}\right)}\:=\:\mathrm{sinh}\:\left(\mathrm{y}\right) \\ $$
