Menu Close

Prove-that-tanx-2-pi-2x-2-pi-2x-2-3x-2pi-2-3x-2pi-2-5x-2pi-2-5x-2pi-

Tinku Tara 0 Comments
Pin




Question Number 122740 by Dwaipayan Shikari last updated on 19/Nov/20
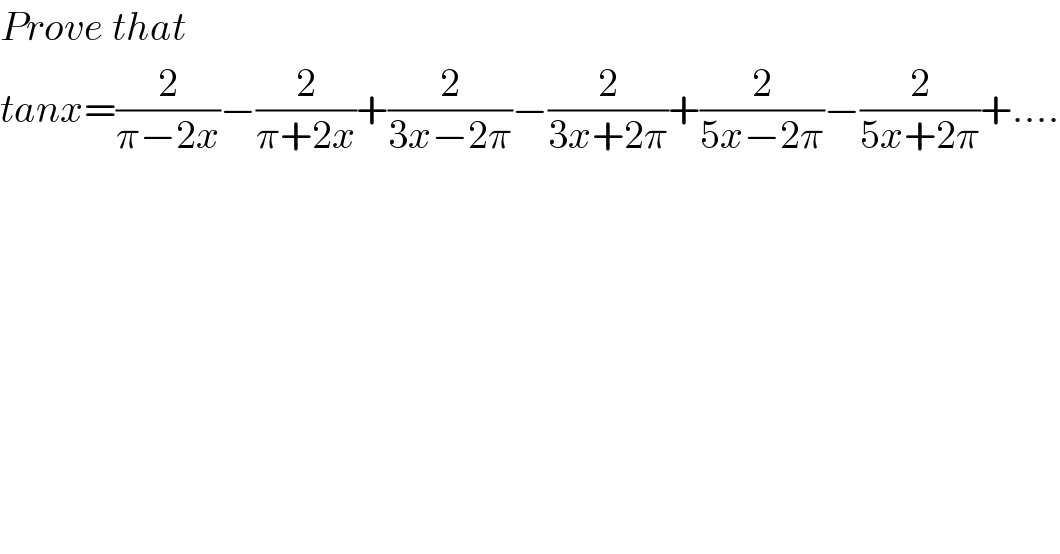
Prove that tanx=(2/(π−2x))−(2/(π+2x))+(2/(3x−2π))−(2/(3x+2π))+(2/(5x−2π))−(2/(5x+2π))+....
$${Prove}\:{that} \\ $$$${tanx}=\frac{\mathrm{2}}{\pi−\mathrm{2}{x}}−\frac{\mathrm{2}}{\pi+\mathrm{2}{x}}+\frac{\mathrm{2}}{\mathrm{3}{x}−\mathrm{2}\pi}−\frac{\mathrm{2}}{\mathrm{3}{x}+\mathrm{2}\pi}+\frac{\mathrm{2}}{\mathrm{5}{x}−\mathrm{2}\pi}−\frac{\mathrm{2}}{\mathrm{5}{x}+\mathrm{2}\pi}+…. \\ $$
Commented by Dwaipayan Shikari last updated on 19/Nov/20
sinx has value 0 at 0,π,−π, 2π,−2π,.... So it can be written as products sinx=Cx(π−x)(x+π)(2π−x)(x+2π)... x→0 ((sinx)/(Cx))=(π−x)(x+π)(2π−x)... ⇒(1/C)=π.π.2π.2π... So sinx=x(1−(x/π))(1+(x/π))(1−(x/(2π)))... ((sinx)/x)=Π_(n=1) ^∞ (1−(x^2 /(n^2 π^2 ))) So in this manner cosx=(1−((2x)/π))(1+((2x)/π))(1−((2x)/(3π)))(1+((2x)/(3π)))... log(cosx)=log(1−((2x)/π))+log(1+((2x)/π))+... −((sinx)/(cosx))=(((−2)/π)/(1−((2x)/π)))+((2/π)/(1+((2x)/π)))−((2/(3π))/(1−((2x)/(3π))))+... tanx=(2/(π−2x))−(2/(π+2x))+(2/(3π−2x))−(2/(3π+2x))+(2/(5π−2x))−(2/(5π+2x))+... tanx=(1/((π/2)−x))−(1/((π/2)+x))+(1/(((3π)/2)−x))−(1/(((3π)/2)+x))+(1/(((5π)/2)−x))−(1/(((5π)/2)+x))+...
$${sinx}\:\:{has}\:{value}\:\mathrm{0}\:{at}\:\mathrm{0},\pi,−\pi,\:\mathrm{2}\pi,−\mathrm{2}\pi,…. \\ $$$${So}\:{it}\:{can}\:{be}\:{written}\:{as}\:{products} \\ $$$${sinx}={Cx}\left(\pi−{x}\right)\left({x}+\pi\right)\left(\mathrm{2}\pi−{x}\right)\left({x}+\mathrm{2}\pi\right)… \\ $$$${x}\rightarrow\mathrm{0}\:\:\frac{{sinx}}{{Cx}}=\left(\pi−{x}\right)\left({x}+\pi\right)\left(\mathrm{2}\pi−{x}\right)… \\ $$$$\Rightarrow\frac{\mathrm{1}}{{C}}=\pi.\pi.\mathrm{2}\pi.\mathrm{2}\pi… \\ $$$${So}\:\:\:{sinx}={x}\left(\mathrm{1}−\frac{{x}}{\pi}\right)\left(\mathrm{1}+\frac{{x}}{\pi}\right)\left(\mathrm{1}−\frac{{x}}{\mathrm{2}\pi}\right)… \\ $$$$\frac{{sinx}}{{x}}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{n}^{\mathrm{2}} \pi^{\mathrm{2}} }\right) \\ $$$${So}\:{in}\:{this}\:{manner}\: \\ $$$${cosx}=\left(\mathrm{1}−\frac{\mathrm{2}{x}}{\pi}\right)\left(\mathrm{1}+\frac{\mathrm{2}{x}}{\pi}\right)\left(\mathrm{1}−\frac{\mathrm{2}{x}}{\mathrm{3}\pi}\right)\left(\mathrm{1}+\frac{\mathrm{2}{x}}{\mathrm{3}\pi}\right)… \\ $$$${log}\left({cosx}\right)={log}\left(\mathrm{1}−\frac{\mathrm{2}{x}}{\pi}\right)+{log}\left(\mathrm{1}+\frac{\mathrm{2}{x}}{\pi}\right)+… \\ $$$$−\frac{{sinx}}{{cosx}}=\frac{\frac{−\mathrm{2}}{\pi}}{\mathrm{1}−\frac{\mathrm{2}{x}}{\pi}}+\frac{\frac{\mathrm{2}}{\pi}}{\mathrm{1}+\frac{\mathrm{2}{x}}{\pi}}−\frac{\frac{\mathrm{2}}{\mathrm{3}\pi}}{\mathrm{1}−\frac{\mathrm{2}{x}}{\mathrm{3}\pi}}+… \\ $$$${tanx}=\frac{\mathrm{2}}{\pi−\mathrm{2}{x}}−\frac{\mathrm{2}}{\pi+\mathrm{2}{x}}+\frac{\mathrm{2}}{\mathrm{3}\pi−\mathrm{2}{x}}−\frac{\mathrm{2}}{\mathrm{3}\pi+\mathrm{2}{x}}+\frac{\mathrm{2}}{\mathrm{5}\pi−\mathrm{2}{x}}−\frac{\mathrm{2}}{\mathrm{5}\pi+\mathrm{2}{x}}+… \\ $$$${tanx}=\frac{\mathrm{1}}{\frac{\pi}{\mathrm{2}}−{x}}−\frac{\mathrm{1}}{\frac{\pi}{\mathrm{2}}+{x}}+\frac{\mathrm{1}}{\frac{\mathrm{3}\pi}{\mathrm{2}}−{x}}−\frac{\mathrm{1}}{\frac{\mathrm{3}\pi}{\mathrm{2}}+{x}}+\frac{\mathrm{1}}{\frac{\mathrm{5}\pi}{\mathrm{2}}−{x}}−\frac{\mathrm{1}}{\frac{\mathrm{5}\pi}{\mathrm{2}}+{x}}+… \\ $$
Commented by Dwaipayan Shikari last updated on 19/Nov/20
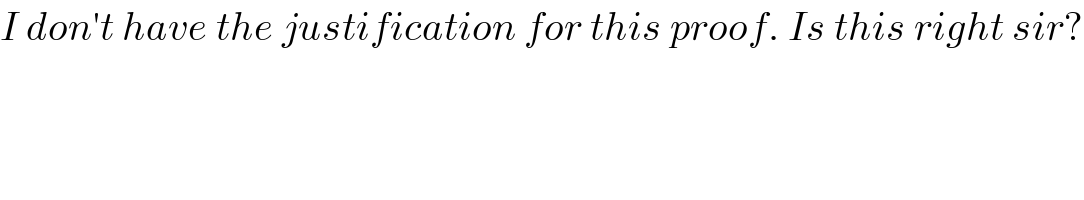
I don′t have the justification for this proof. Is this right sir?
$${I}\:{don}'{t}\:{have}\:{the}\:{justification}\:{for}\:{this}\:{proof}.\:{Is}\:{this}\:{right}\:{sir}? \\ $$
Commented by mindispower last updated on 19/Nov/20
cos(x)=sin((π/2)−x) (d/dx)lncos(x)=−tg(x)
$${cos}\left({x}\right)={sin}\left(\frac{\pi}{\mathrm{2}}−{x}\right) \\ $$$$\frac{{d}}{{dx}}{lncos}\left({x}\right)=−{tg}\left({x}\right) \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *