Prove-that-the-angular-momentum-H-G-of-a-rigid-body-about-its-mass-center-is-given-by-H-x-I-x-x-I-xy-y-I-xz-z-H-y-I-yx-x-I-y-y-I-yz-z-H-z-I-zx-

Question Number 27986 by ajfour last updated on 18/Jan/18

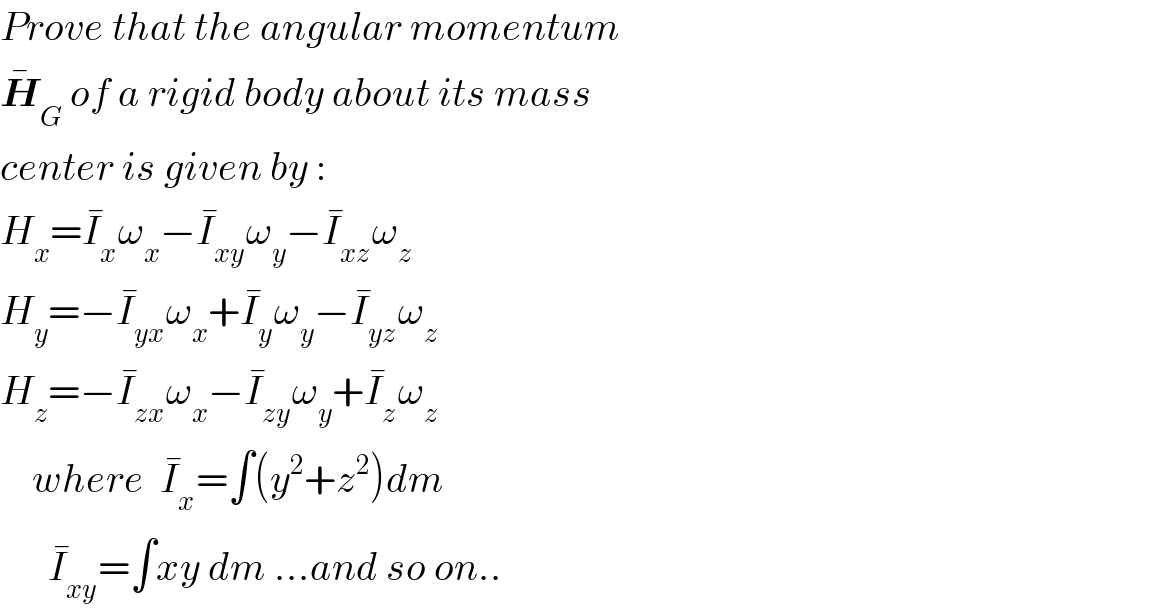
P r o v e t h a t t h e a n g u l a r m o m e n t u m

{\bar{H}}_{G} o f a r i g i d b o d y a b o u t i t s m a s s

c e n t e r i s g i v e n b y :

H_{x} = {\bar{I}}_{x} ω_{x} - {\bar{I}}_{x y} ω_{y} - {\bar{I}}_{x z} ω_{z}

H_{y} = - {\bar{I}}_{y x} ω_{x} + {\bar{I}}_{y} ω_{y} - {\bar{I}}_{y z} ω_{z}

H_{z} = - {\bar{I}}_{z x} ω_{x} - {\bar{I}}_{z y} ω_{y} + {\bar{I}}_{z} ω_{z}

w h e r e {\bar{I}}_{x} = \int (y^{2} + z^{2}) d m

{\bar{I}}_{x y} = \int x y d m \dots a n d s o o n . .

Commented by ajfour last updated on 22/Mar/19

?

Facebook Tweet Pin