Question Number 22316 by Tinkutara last updated on 15/Oct/17
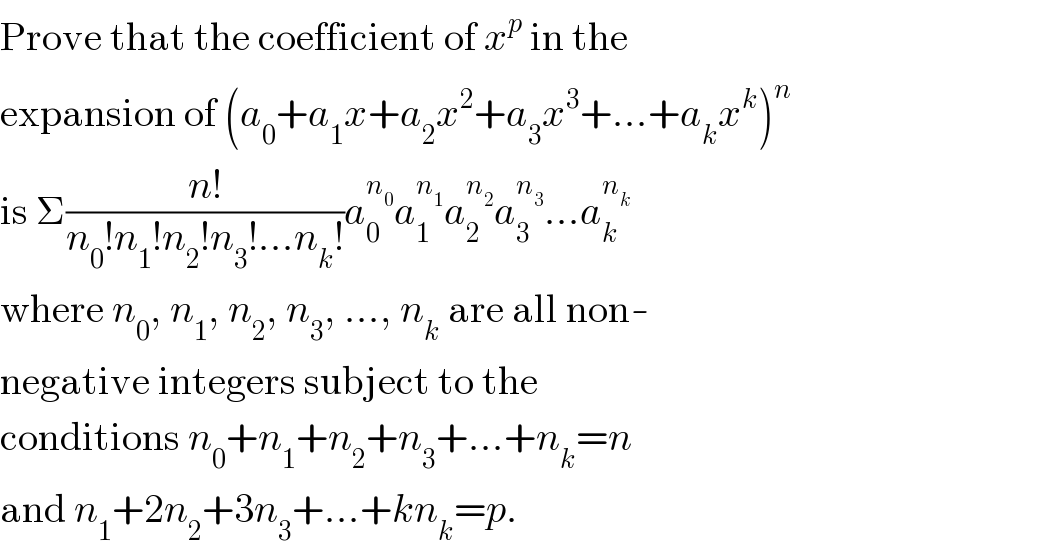
$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{coefficient}\:\mathrm{of}\:{x}^{{p}} \:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{expansion}\:\mathrm{of}\:\left({a}_{\mathrm{0}} +{a}_{\mathrm{1}} {x}+{a}_{\mathrm{2}} {x}^{\mathrm{2}} +{a}_{\mathrm{3}} {x}^{\mathrm{3}} +…+{a}_{{k}} {x}^{{k}} \right)^{{n}} \\ $$$$\mathrm{is}\:\Sigma\frac{{n}!}{{n}_{\mathrm{0}} !{n}_{\mathrm{1}} !{n}_{\mathrm{2}} !{n}_{\mathrm{3}} !…{n}_{{k}} !}{a}_{\mathrm{0}} ^{{n}_{\mathrm{0}} } {a}_{\mathrm{1}} ^{{n}_{\mathrm{1}} } {a}_{\mathrm{2}} ^{{n}_{\mathrm{2}} } {a}_{\mathrm{3}} ^{{n}_{\mathrm{3}} } …{a}_{{k}} ^{{n}_{{k}} } \\ $$$$\mathrm{where}\:{n}_{\mathrm{0}} ,\:{n}_{\mathrm{1}} ,\:{n}_{\mathrm{2}} ,\:{n}_{\mathrm{3}} ,\:…,\:{n}_{{k}} \:\mathrm{are}\:\mathrm{all}\:\mathrm{non}- \\ $$$$\mathrm{negative}\:\mathrm{integers}\:\mathrm{subject}\:\mathrm{to}\:\mathrm{the} \\ $$$$\mathrm{conditions}\:{n}_{\mathrm{0}} +{n}_{\mathrm{1}} +{n}_{\mathrm{2}} +{n}_{\mathrm{3}} +…+{n}_{{k}} ={n} \\ $$$$\mathrm{and}\:{n}_{\mathrm{1}} +\mathrm{2}{n}_{\mathrm{2}} +\mathrm{3}{n}_{\mathrm{3}} +…+{kn}_{{k}} ={p}. \\ $$
