Prove-that-the-curve-y-x-4-3x-2-2x-does-not-meet-the-straight-line-y-2x-1-and-find-the-distace-between-their-nearest-points-Answer-1-5-

Question Number 105456 by 1549442205PVT last updated on 29/Jul/20

Prove that the curve y = x^{4} + {3 x}^{2} + 2 x

does not meet the straight line

y = 2 x - 1 and find the distace between

their nearest points . (Answer \frac{1}{\sqrt{5}})

Answered by ajfour last updated on 29/Jul/20

l e t y = 2 x + c b e t a n g e n t t o c u r v e

\Rightarrow \frac{d y}{d x} = 4 x^{3} + 6 x + 2 = \frac{d}{d x} (2 x - 1)

\Rightarrow x = 0, y = 0

N o w ⊥ d i s t a n c e o f (0, 0) f r o m

y = 2 x - 1 i s

p = \frac{1}{\sqrt{5}} .

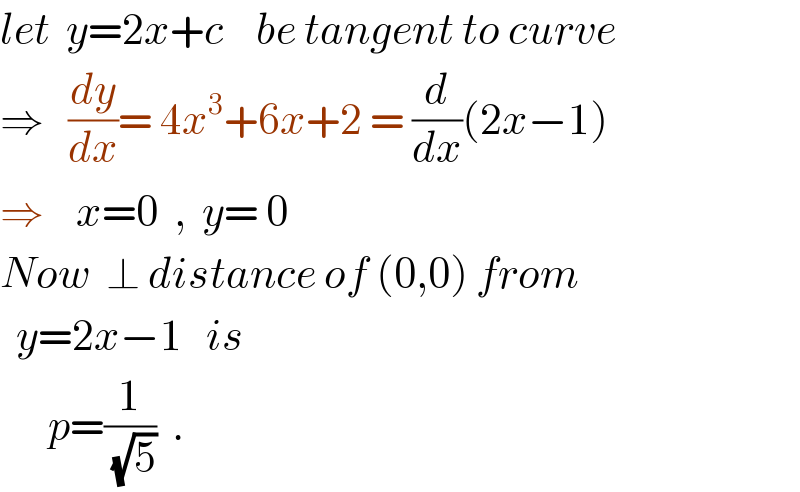
Commented by Ari last updated on 29/Jul/20

Sir, if you can, clarify through actions your reasoning that there is ambiguity

Commented by 1549442205PVT last updated on 29/Jul/20

Thank you both sir .

Answered by 1549442205PVT last updated on 29/Jul/20

i) Abscissa of intersection point of the curve

y = x^{4} + {3 x}^{2} + 2 x (C) and the line y = 2 x - 1 (L)

must be a real root of the equation :

x^{4} + {3 x}^{2} + 2 x = 2 x - 1 \Leftrightarrow x^{4} + {3 x}^{2} + 1 = 0

But this equation has no real roots

simce x^{4} + {3 x}^{2} + 1 ⩾ 1 \forall x \in R . Hence the

curve (C) {don}^{'} t meet the line (L) (q . e . d)

ii) Denote by A (x_{0}, y_{0}) be a point at

which the tangent of the curve parallel

to the line y = 2 x + 1 . Then

{(x^{4} + {3 x}^{2} + 2 x)}^{^{'}} ∣_{x_{0}} = 2 \Leftrightarrow {4 x}_{0}^{3} + {6 x}_{0} + 2 = 2

\Leftrightarrow {2 x}_{0} ({2 x}_{0}^{2} + 3) = 0 \Leftrightarrow x_{0} = 0 \Rightarrow y_{0} = 0 . Then

the nearest distance between the curve

and the line be the distance between

A (x_{0}, y_{0}) and the line y = 2 x - 1 which

means d_{0} = \frac{∣ 2.0 - 1.0 ∣}{\sqrt{2^{2} + 1^{2}}} = \frac{1}{\sqrt{5}}

Commented by Ari last updated on 29/Jul/20

you are right