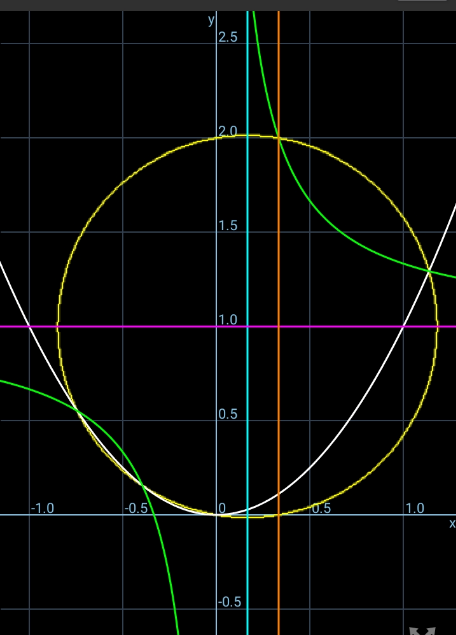
Question Number 118634 by ajfour last updated on 18/Oct/20
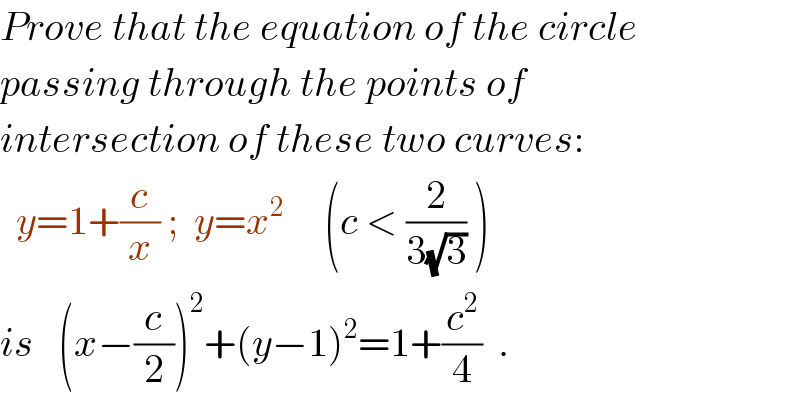
$${Prove}\:{that}\:{the}\:{equation}\:{of}\:{the}\:{circle} \\ $$$${passing}\:{through}\:{the}\:{points}\:{of} \\ $$$${intersection}\:{of}\:{these}\:{two}\:{curves}: \\ $$$$\:\:{y}=\mathrm{1}+\frac{{c}}{{x}}\:;\:\:{y}={x}^{\mathrm{2}} \:\:\:\:\:\left({c}\:<\:\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}\:\right)\: \\ $$$${is}\:\:\:\left({x}−\frac{{c}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1}+\frac{{c}^{\mathrm{2}} }{\mathrm{4}}\:\:. \\ $$
Commented by necxxx last updated on 18/Oct/20

$${sir}\:{Ajfour},\:{you}\:{and}\:{I}\:{know}\:{these}\:{your} \\ $$$${qudstions}\:{are}\:{for}\:{MrW}\:{and}\:{B}.{e}.{h}.{i}\:…{lol} \\ $$$${I}\:{really}\:{appreciate}\:{your}\:{questions};\:{they} \\ $$$${remind}\:{me}\:{that}\:{there}'{s}\:{more}\:{to}\:{what}\:{we} \\ $$$${ever}\:{know}. \\ $$
Commented by ajfour last updated on 18/Oct/20
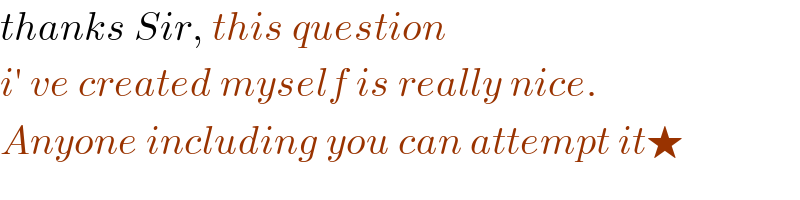
$${thanks}\:{Sir},\:{this}\:{question} \\ $$$${i}'\:{ve}\:{created}\:{myself}\:{is}\:{really}\:{nice}. \\ $$$${Anyone}\:{including}\:{you}\:{can}\:{attempt}\:{it}\bigstar \\ $$
Commented by ajfour last updated on 18/Oct/20