Question Number 81470 by ajfour last updated on 13/Feb/20

$${Prove}\:{that}\:{the}\:{locus}\:{of}\:{the}\:{point} \\ $$$${of}\:{intersection}\:{of}\:{perpendicular} \\ $$$${tangents}\:{to}\:{an}\:{ellipse}\:{is}\:{another} \\ $$$${ellipse}. \\ $$
Answered by mr W last updated on 13/Feb/20
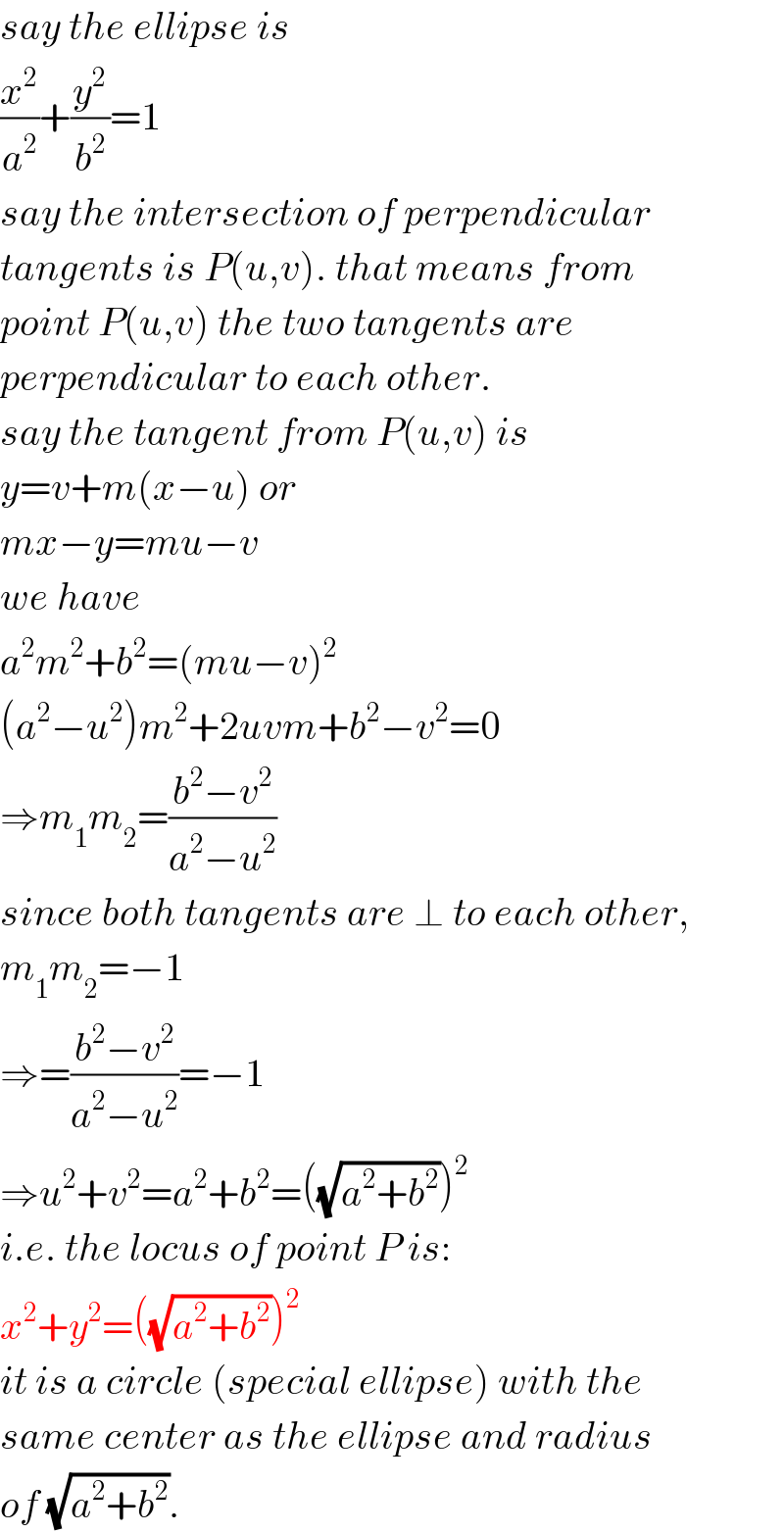
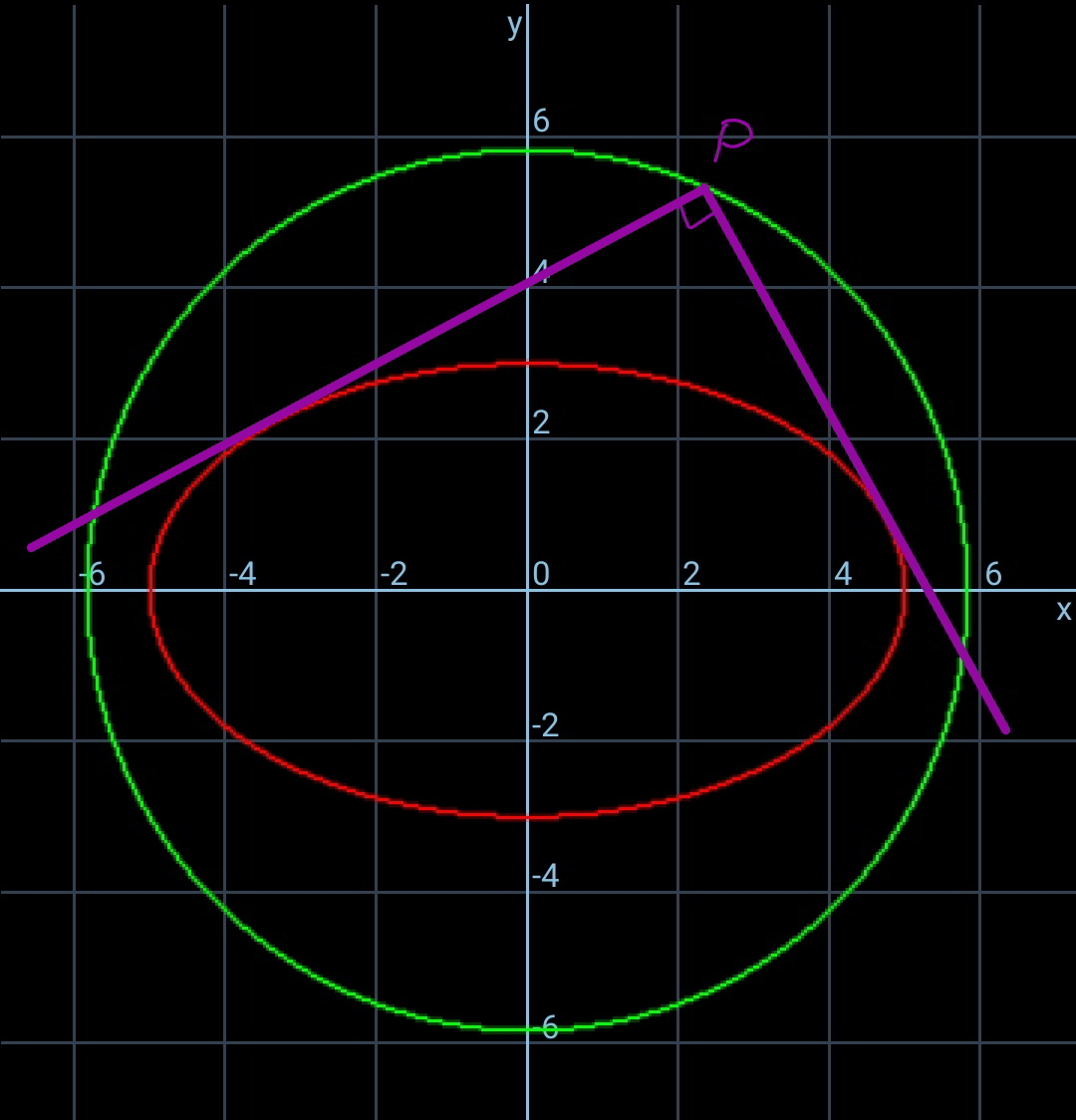
$${say}\:{the}\:{ellipse}\:{is} \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${say}\:{the}\:{intersection}\:{of}\:{perpendicular} \\ $$$${tangents}\:{is}\:{P}\left({u},{v}\right).\:{that}\:{means}\:{from} \\ $$$${point}\:{P}\left({u},{v}\right)\:{the}\:{two}\:{tangents}\:{are} \\ $$$${perpendicular}\:{to}\:{each}\:{other}. \\ $$$${say}\:{the}\:{tangent}\:{from}\:{P}\left({u},{v}\right)\:{is} \\ $$$${y}={v}+{m}\left({x}−{u}\right)\:{or} \\ $$$${mx}−{y}={mu}−{v} \\ $$$${we}\:{have} \\ $$$${a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} =\left({mu}−{v}\right)^{\mathrm{2}} \\ $$$$\left({a}^{\mathrm{2}} −{u}^{\mathrm{2}} \right){m}^{\mathrm{2}} +\mathrm{2}{uvm}+{b}^{\mathrm{2}} −{v}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{m}_{\mathrm{1}} {m}_{\mathrm{2}} =\frac{{b}^{\mathrm{2}} −{v}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{u}^{\mathrm{2}} } \\ $$$${since}\:{both}\:{tangents}\:{are}\:\bot\:{to}\:{each}\:{other}, \\ $$$${m}_{\mathrm{1}} {m}_{\mathrm{2}} =−\mathrm{1} \\ $$$$\Rightarrow=\frac{{b}^{\mathrm{2}} −{v}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{u}^{\mathrm{2}} }=−\mathrm{1} \\ $$$$\Rightarrow{u}^{\mathrm{2}} +{v}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\left(\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$${i}.{e}.\:{the}\:{locus}\:{of}\:{point}\:{P}\:{is}: \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\left(\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$${it}\:{is}\:{a}\:{circle}\:\left({special}\:{ellipse}\right)\:{with}\:{the} \\ $$$${same}\:{center}\:{as}\:{the}\:{ellipse}\:{and}\:{radius} \\ $$$${of}\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }. \\ $$
Commented by mr W last updated on 13/Feb/20
Commented by ajfour last updated on 13/Feb/20

$${Thanks}\:{Sir},\:{but}\:{thats}\:{how}\:{the} \\ $$$${question}\:{was}\:{written}\:{in}\:{a}\:{book}! \\ $$
Commented by mr W last updated on 13/Feb/20
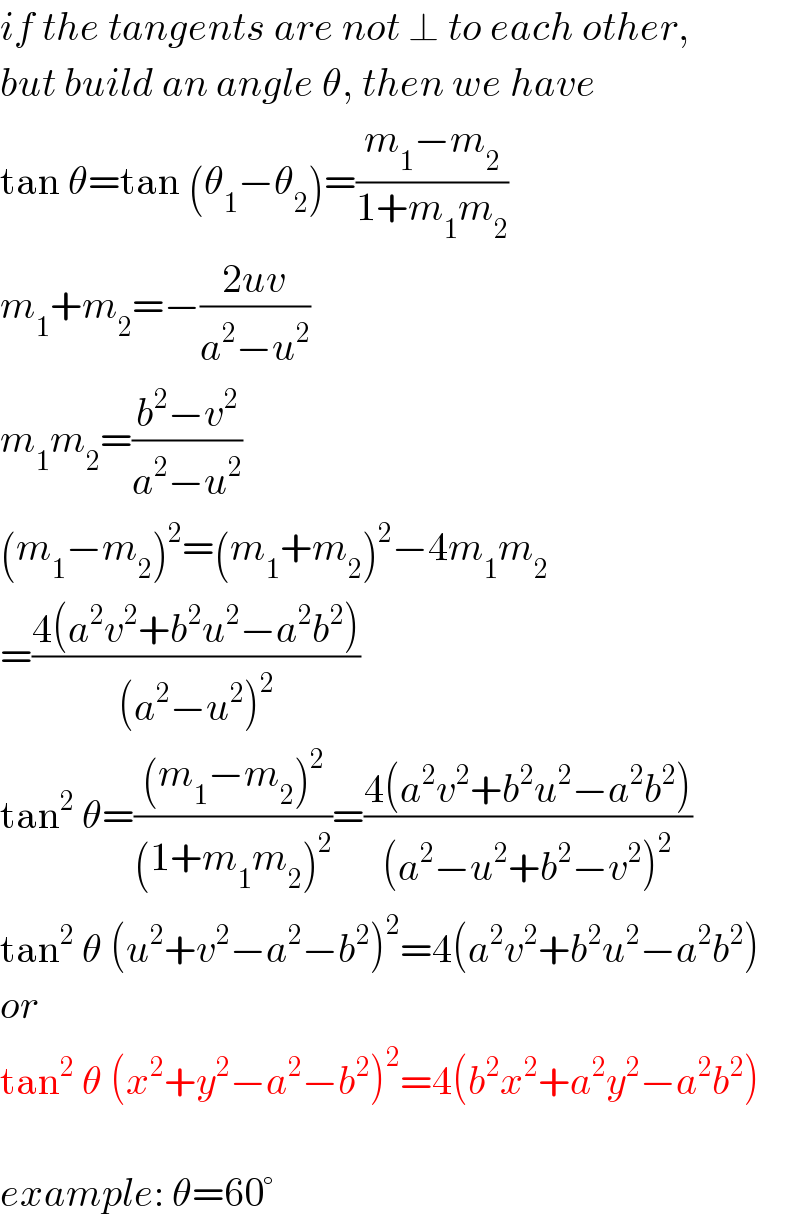
$${if}\:{the}\:{tangents}\:{are}\:{not}\:\bot\:{to}\:{each}\:{other}, \\ $$$${but}\:{build}\:{an}\:{angle}\:\theta,\:{then}\:{we}\:{have} \\ $$$$\mathrm{tan}\:\theta=\mathrm{tan}\:\left(\theta_{\mathrm{1}} −\theta_{\mathrm{2}} \right)=\frac{{m}_{\mathrm{1}} −{m}_{\mathrm{2}} }{\mathrm{1}+{m}_{\mathrm{1}} {m}_{\mathrm{2}} } \\ $$$${m}_{\mathrm{1}} +{m}_{\mathrm{2}} =−\frac{\mathrm{2}{uv}}{{a}^{\mathrm{2}} −{u}^{\mathrm{2}} } \\ $$$${m}_{\mathrm{1}} {m}_{\mathrm{2}} =\frac{{b}^{\mathrm{2}} −{v}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{u}^{\mathrm{2}} } \\ $$$$\left({m}_{\mathrm{1}} −{m}_{\mathrm{2}} \right)^{\mathrm{2}} =\left({m}_{\mathrm{1}} +{m}_{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}{m}_{\mathrm{1}} {m}_{\mathrm{2}} \\ $$$$=\frac{\mathrm{4}\left({a}^{\mathrm{2}} {v}^{\mathrm{2}} +{b}^{\mathrm{2}} {u}^{\mathrm{2}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right)}{\left({a}^{\mathrm{2}} −{u}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\mathrm{tan}^{\mathrm{2}} \:\theta=\frac{\left({m}_{\mathrm{1}} −{m}_{\mathrm{2}} \right)^{\mathrm{2}} }{\left(\mathrm{1}+{m}_{\mathrm{1}} {m}_{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{\mathrm{4}\left({a}^{\mathrm{2}} {v}^{\mathrm{2}} +{b}^{\mathrm{2}} {u}^{\mathrm{2}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right)}{\left({a}^{\mathrm{2}} −{u}^{\mathrm{2}} +{b}^{\mathrm{2}} −{v}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\mathrm{tan}^{\mathrm{2}} \:\theta\:\left({u}^{\mathrm{2}} +{v}^{\mathrm{2}} −{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{4}\left({a}^{\mathrm{2}} {v}^{\mathrm{2}} +{b}^{\mathrm{2}} {u}^{\mathrm{2}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right) \\ $$$${or} \\ $$$$\mathrm{tan}^{\mathrm{2}} \:\theta\:\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} −{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{4}\left({b}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}^{\mathrm{2}} {y}^{\mathrm{2}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right) \\ $$$$ \\ $$$${example}:\:\theta=\mathrm{60}° \\ $$
Commented by mr W last updated on 13/Feb/20
$${i}\:{made}\:{a}\:{mistake}.\:{now}\:{it}\:{should}\:{be} \\ $$$${correct}. \\ $$
Commented by ajfour last updated on 13/Feb/20
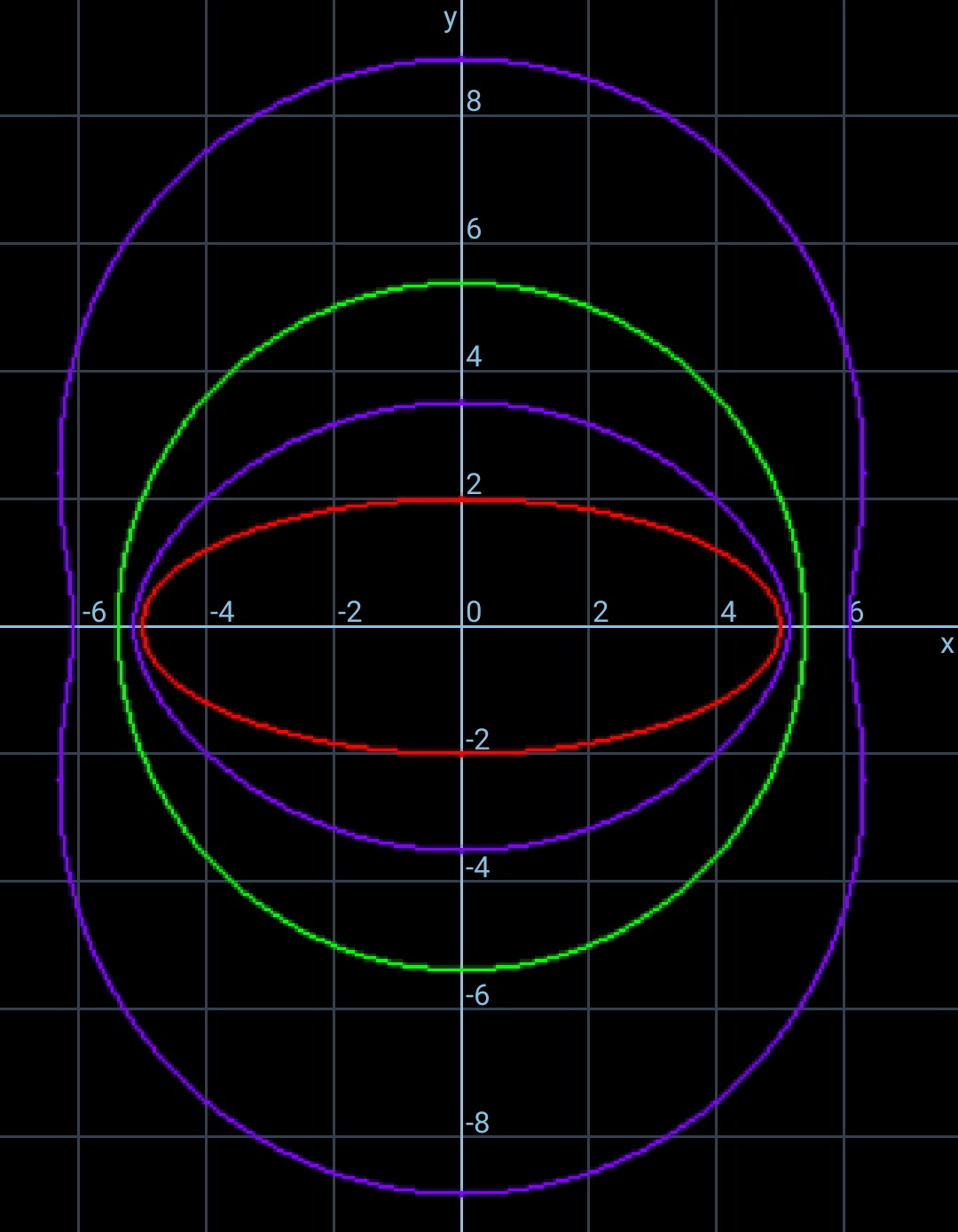
$${Beautiful}\:! \\ $$$${how}\:{come}\:{the}\:{blue}\:{curves}\:{dont} \\ $$$${meet}\:{the}\:{x}-{axis},\:{Sir}? \\ $$$$ \\ $$
Commented by mr W last updated on 13/Feb/20
Commented by ajfour last updated on 14/Feb/20

$${thanks}\:{sir},\:{for}\:{taking}\:{my} \\ $$$${remark}\:{seriously},\:{now}\:{it} \\ $$$${seems}\:{more}\:{natural}\:{type}.. \\ $$
