Menu Close

prove-that-x-2-e-x-2-cos-x-2-sin-x-2-dx-pi-sin-3-tan-1-2-2-4-125-1-4-

Tinku Tara 0 Comments
Pin




Question Number 129764 by Eric002 last updated on 18/Jan/21
prove that ∫_(−∞) ^(+∞) x^2 e^(−x^2 ) cos(x^2 )sin(x^2 ) dx =(((√π)sin[(((√3)tan^(−1) (2))/2)])/(4 ((125))^(1/4) ))
$${prove}\:{that} \\ $$$$\int_{−\infty} ^{+\infty} {x}^{\mathrm{2}} \:{e}^{−{x}^{\mathrm{2}} } \:{cos}\left({x}^{\mathrm{2}} \right){sin}\left({x}^{\mathrm{2}} \right)\:{dx} \\ $$$$=\frac{\sqrt{\pi}{sin}\left[\frac{\sqrt{\mathrm{3}}{tan}^{−\mathrm{1}} \left(\mathrm{2}\right)}{\mathrm{2}}\right]}{\mathrm{4}\:\sqrt[{\mathrm{4}}]{\mathrm{125}}} \\ $$
Answered by Dwaipayan Shikari last updated on 18/Jan/21
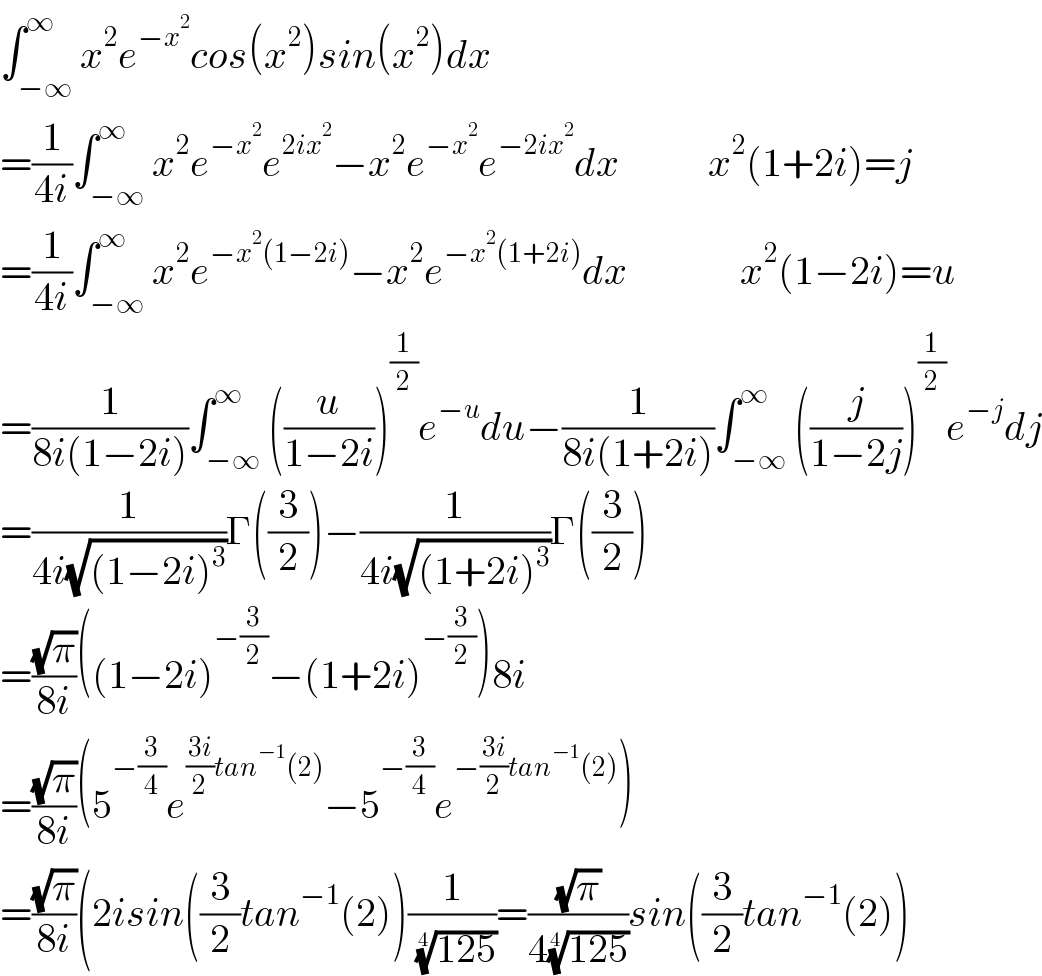
∫_(−∞) ^∞ x^2 e^(−x^2 ) cos(x^2 )sin(x^2 )dx =(1/(4i))∫_(−∞) ^∞ x^2 e^(−x^2 ) e^(2ix^2 ) −x^2 e^(−x^2 ) e^(−2ix^2 ) dx x^2 (1+2i)=j =(1/(4i))∫_(−∞) ^∞ x^2 e^(−x^2 (1−2i)) −x^2 e^(−x^2 (1+2i)) dx x^2 (1−2i)=u =(1/(8i(1−2i)))∫_(−∞) ^∞ ((u/(1−2i)))^(1/2) e^(−u) du−(1/(8i(1+2i)))∫_(−∞) ^∞ ((j/(1−2j)))^(1/2) e^(−j) dj =(1/(4i(√((1−2i)^3 ))))Γ((3/2))−(1/(4i(√((1+2i)^3 ))))Γ((3/2)) =((√π)/(8i))((1−2i)^(−(3/2)) −(1+2i)^(−(3/2)) )8i =((√π)/(8i))(5^(−(3/4)) e^(((3i)/2)tan^(−1) (2)) −5^(−(3/4)) e^(−((3i)/2)tan^(−1) (2)) ) =((√π)/(8i))(2isin((3/2)tan^(−1) (2))(1/( ((125))^(1/4) ))=((√π)/(4((125))^(1/4) ))sin((3/2)tan^(−1) (2))
$$\int_{−\infty} ^{\infty} {x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{2}} } {cos}\left({x}^{\mathrm{2}} \right){sin}\left({x}^{\mathrm{2}} \right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}{i}}\int_{−\infty} ^{\infty} {x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{2}} } {e}^{\mathrm{2}{ix}^{\mathrm{2}} } −{x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{2}} } {e}^{−\mathrm{2}{ix}^{\mathrm{2}} } {dx}\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{2}{i}\right)={j} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}{i}}\int_{−\infty} ^{\infty} {x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{2}{i}\right)} −{x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{2}{i}\right)} {dx}\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{2}{i}\right)={u} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}{i}\left(\mathrm{1}−\mathrm{2}{i}\right)}\int_{−\infty} ^{\infty} \left(\frac{{u}}{\mathrm{1}−\mathrm{2}{i}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {e}^{−{u}} {du}−\frac{\mathrm{1}}{\mathrm{8}{i}\left(\mathrm{1}+\mathrm{2}{i}\right)}\int_{−\infty} ^{\infty} \left(\frac{{j}}{\mathrm{1}−\mathrm{2}{j}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {e}^{−{j}} {dj} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}{i}\sqrt{\left(\mathrm{1}−\mathrm{2}{i}\right)^{\mathrm{3}} }}\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{4}{i}\sqrt{\left(\mathrm{1}+\mathrm{2}{i}\right)^{\mathrm{3}} }}\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{8}{i}}\left(\left(\mathrm{1}−\mathrm{2}{i}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} −\left(\mathrm{1}+\mathrm{2}{i}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \right)\mathrm{8}{i} \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{8}{i}}\left(\mathrm{5}^{−\frac{\mathrm{3}}{\mathrm{4}}} {e}^{\frac{\mathrm{3}{i}}{\mathrm{2}}{tan}^{−\mathrm{1}} \left(\mathrm{2}\right)} −\mathrm{5}^{−\frac{\mathrm{3}}{\mathrm{4}}} {e}^{−\frac{\mathrm{3}{i}}{\mathrm{2}}{tan}^{−\mathrm{1}} \left(\mathrm{2}\right)} \right) \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{8}{i}}\left(\mathrm{2}{isin}\left(\frac{\mathrm{3}}{\mathrm{2}}{tan}^{−\mathrm{1}} \left(\mathrm{2}\right)\right)\frac{\mathrm{1}}{\:\sqrt[{\mathrm{4}}]{\mathrm{125}}}=\frac{\sqrt{\pi}}{\mathrm{4}\sqrt[{\mathrm{4}}]{\mathrm{125}}}{sin}\left(\frac{\mathrm{3}}{\mathrm{2}}{tan}^{−\mathrm{1}} \left(\mathrm{2}\right)\right)\right. \\ $$
Commented by Eric002 last updated on 18/Jan/21
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Answered by mathmax by abdo last updated on 18/Jan/21
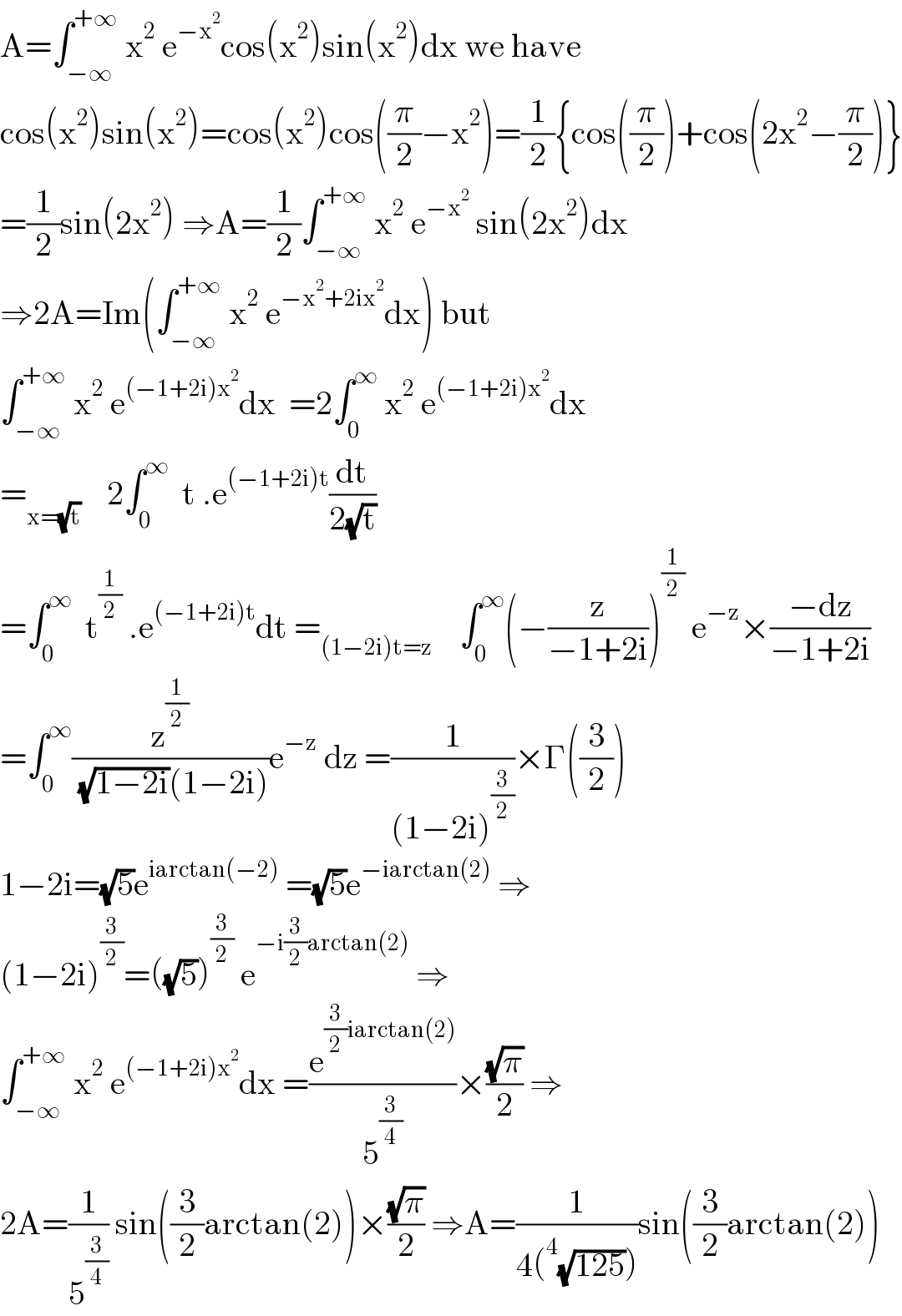
A=∫_(−∞) ^(+∞) x^2 e^(−x^2 ) cos(x^2 )sin(x^2 )dx we have cos(x^2 )sin(x^2 )=cos(x^2 )cos((π/2)−x^2 )=(1/2){cos((π/2))+cos(2x^2 −(π/2))} =(1/2)sin(2x^2 ) ⇒A=(1/2)∫_(−∞) ^(+∞) x^2 e^(−x^2 ) sin(2x^2 )dx ⇒2A=Im(∫_(−∞) ^(+∞) x^2 e^(−x^2 +2ix^2 ) dx) but ∫_(−∞) ^(+∞) x^2 e^((−1+2i)x^2 ) dx =2∫_0 ^∞ x^2 e^((−1+2i)x^2 ) dx =_(x=(√t)) 2∫_0 ^∞ t .e^((−1+2i)t) (dt/(2(√t))) =∫_0 ^∞ t^(1/2) .e^((−1+2i)t) dt =_((1−2i)t=z) ∫_0 ^∞ (−(z/(−1+2i)))^(1/2) e^(−z) ×((−dz)/(−1+2i)) =∫_0 ^∞ (z^(1/2) /( (√(1−2i))(1−2i)))e^(−z) dz =(1/((1−2i)^(3/2) ))×Γ((3/2)) 1−2i=(√5)e^(iarctan(−2)) =(√5)e^(−iarctan(2)) ⇒ (1−2i)^(3/2) =((√5))^(3/2) e^(−i(3/2)arctan(2)) ⇒ ∫_(−∞) ^(+∞) x^2 e^((−1+2i)x^2 ) dx =(e^((3/2)iarctan(2)) /5^(3/4) )×((√π)/2) ⇒ 2A=(1/5^(3/4) ) sin((3/2)arctan(2))×((√π)/2) ⇒A=(1/(4(^4 (√(125)))))sin((3/2)arctan(2))
$$\mathrm{A}=\int_{−\infty} ^{+\infty} \:\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{cos}\left(\mathrm{x}^{\mathrm{2}} \right)\mathrm{sin}\left(\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{cos}\left(\mathrm{x}^{\mathrm{2}} \right)\mathrm{sin}\left(\mathrm{x}^{\mathrm{2}} \right)=\mathrm{cos}\left(\mathrm{x}^{\mathrm{2}} \right)\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{x}^{\mathrm{2}} \right)=\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}\right)+\mathrm{cos}\left(\mathrm{2x}^{\mathrm{2}} −\frac{\pi}{\mathrm{2}}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2x}^{\mathrm{2}} \right)\:\Rightarrow\mathrm{A}=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \:\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \:\mathrm{sin}\left(\mathrm{2x}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$\Rightarrow\mathrm{2A}=\mathrm{Im}\left(\int_{−\infty} ^{+\infty} \:\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} +\mathrm{2ix}^{\mathrm{2}} } \mathrm{dx}\right)\:\mathrm{but} \\ $$$$\int_{−\infty} ^{+\infty} \:\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{\left(−\mathrm{1}+\mathrm{2i}\right)\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\:\:=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{\left(−\mathrm{1}+\mathrm{2i}\right)\mathrm{x}^{\mathrm{2}} } \mathrm{dx} \\ $$$$=_{\mathrm{x}=\sqrt{\mathrm{t}}} \:\:\:\:\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{t}\:.\mathrm{e}^{\left(−\mathrm{1}+\mathrm{2i}\right)\mathrm{t}} \frac{\mathrm{dt}}{\mathrm{2}\sqrt{\mathrm{t}}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{2}}} \:.\mathrm{e}^{\left(−\mathrm{1}+\mathrm{2i}\right)\mathrm{t}} \mathrm{dt}\:=_{\left(\mathrm{1}−\mathrm{2i}\right)\mathrm{t}=\mathrm{z}} \:\:\:\:\int_{\mathrm{0}} ^{\infty} \left(−\frac{\mathrm{z}}{−\mathrm{1}+\mathrm{2i}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{e}^{−\mathrm{z}} ×\frac{−\mathrm{dz}}{−\mathrm{1}+\mathrm{2i}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{z}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\:\sqrt{\mathrm{1}−\mathrm{2i}}\left(\mathrm{1}−\mathrm{2i}\right)}\mathrm{e}^{−\mathrm{z}} \:\mathrm{dz}\:=\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{2i}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }×\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$\mathrm{1}−\mathrm{2i}=\sqrt{\mathrm{5}}\mathrm{e}^{\mathrm{iarctan}\left(−\mathrm{2}\right)} \:=\sqrt{\mathrm{5}}\mathrm{e}^{−\mathrm{iarctan}\left(\mathrm{2}\right)} \:\Rightarrow \\ $$$$\left(\mathrm{1}−\mathrm{2i}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} =\left(\sqrt{\mathrm{5}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{e}^{−\mathrm{i}\frac{\mathrm{3}}{\mathrm{2}}\mathrm{arctan}\left(\mathrm{2}\right)} \:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{\left(−\mathrm{1}+\mathrm{2i}\right)\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\:=\frac{\mathrm{e}^{\frac{\mathrm{3}}{\mathrm{2}}\mathrm{iarctan}\left(\mathrm{2}\right)} }{\mathrm{5}^{\frac{\mathrm{3}}{\mathrm{4}}} }×\frac{\sqrt{\pi}}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{2A}=\frac{\mathrm{1}}{\mathrm{5}^{\frac{\mathrm{3}}{\mathrm{4}}} }\:\mathrm{sin}\left(\frac{\mathrm{3}}{\mathrm{2}}\mathrm{arctan}\left(\mathrm{2}\right)\right)×\frac{\sqrt{\pi}}{\mathrm{2}}\:\Rightarrow\mathrm{A}=\frac{\mathrm{1}}{\mathrm{4}\left(^{\mathrm{4}} \sqrt{\mathrm{125}}\right)}\mathrm{sin}\left(\frac{\mathrm{3}}{\mathrm{2}}\mathrm{arctan}\left(\mathrm{2}\right)\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *