Question Number 157268 by gsk2684 last updated on 21/Oct/21
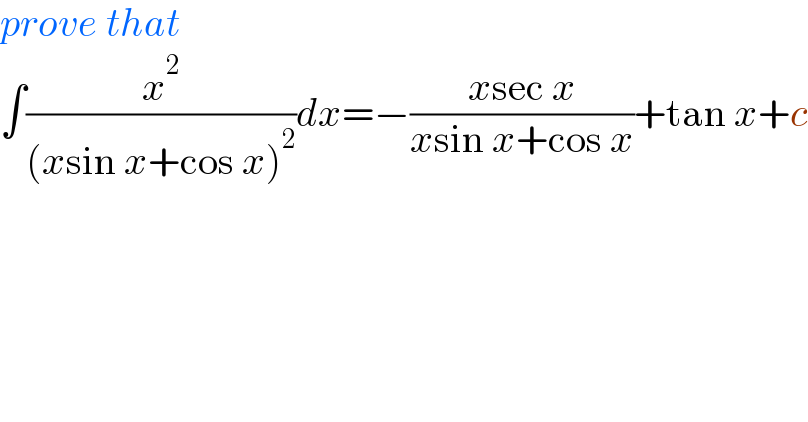
$${prove}\:{that} \\ $$$$\int\frac{{x}^{\mathrm{2}} }{\left({x}\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} }{dx}=−\frac{{x}\mathrm{sec}\:{x}}{{x}\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}+\mathrm{tan}\:{x}+{c} \\ $$
Answered by Ar Brandon last updated on 18/Nov/21
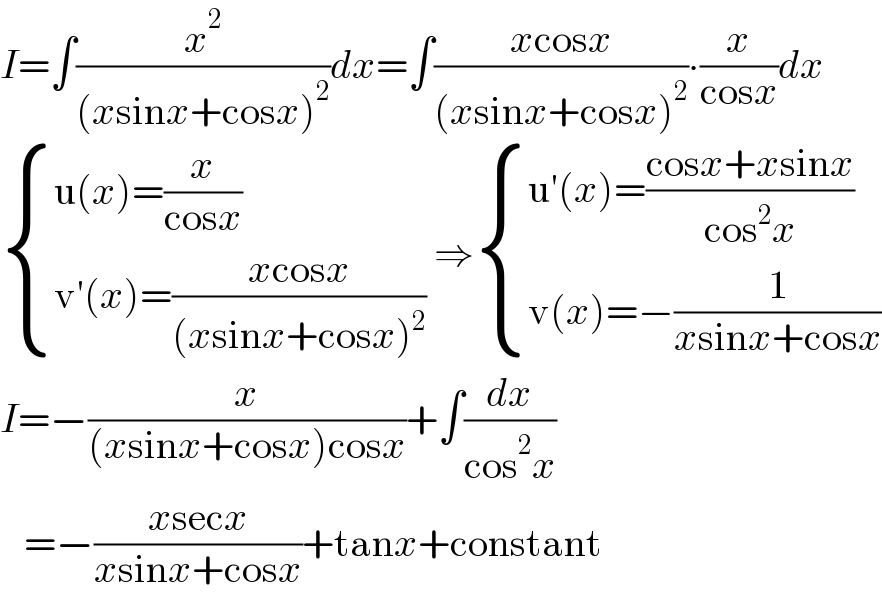
$${I}=\int\frac{{x}^{\mathrm{2}} }{\left({x}\mathrm{sin}{x}+\mathrm{cos}{x}\right)^{\mathrm{2}} }{dx}=\int\frac{{x}\mathrm{cos}{x}}{\left({x}\mathrm{sin}{x}+\mathrm{cos}{x}\right)^{\mathrm{2}} }\centerdot\frac{{x}}{\mathrm{cos}{x}}{dx} \\ $$$$\begin{cases}{\mathrm{u}\left({x}\right)=\frac{{x}}{\mathrm{cos}{x}}}\\{\mathrm{v}'\left({x}\right)=\frac{{x}\mathrm{cos}{x}}{\left({x}\mathrm{sin}{x}+\mathrm{cos}{x}\right)^{\mathrm{2}} }}\end{cases}\:\Rightarrow\begin{cases}{\mathrm{u}'\left({x}\right)=\frac{\mathrm{cos}{x}+{x}\mathrm{sin}{x}}{\mathrm{cos}^{\mathrm{2}} {x}}}\\{\mathrm{v}\left({x}\right)=−\frac{\mathrm{1}}{{x}\mathrm{sin}{x}+\mathrm{cos}{x}}}\end{cases} \\ $$$${I}=−\frac{{x}}{\left({x}\mathrm{sin}{x}+\mathrm{cos}{x}\right)\mathrm{cos}{x}}+\int\frac{{dx}}{\mathrm{cos}^{\mathrm{2}} {x}} \\ $$$$\:\:\:=−\frac{{x}\mathrm{sec}{x}}{{x}\mathrm{sin}{x}+\mathrm{cos}{x}}+\mathrm{tan}{x}+\mathrm{constant} \\ $$
Commented by gsk2684 last updated on 21/Oct/21

$${thank}\:{you} \\ $$
