Menu Close

prove-that-z-0-e-x-x-z-1-dx-Re-z-gt-0-

Tinku Tara 0 Comments
Pin




Question Number 87876 by M±th+et£s last updated on 06/Apr/20
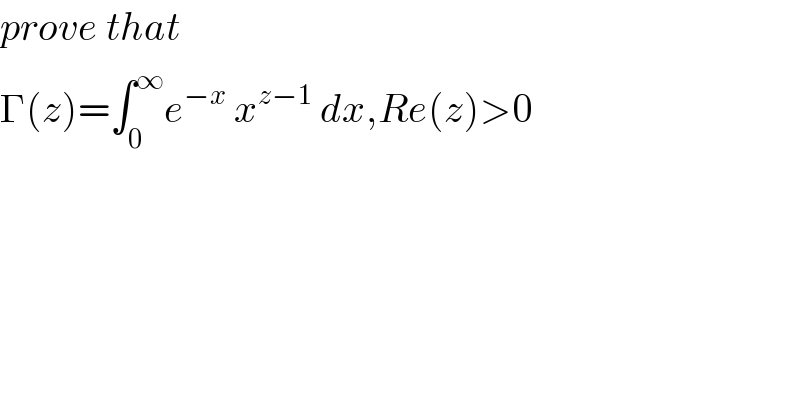
prove that Γ(z)=∫_0 ^∞ e^(−x) x^(z−1) dx,Re(z)>0
$${prove}\:{that} \\ $$$$\Gamma\left({z}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} \:{x}^{{z}−\mathrm{1}} \:{dx},{Re}\left({z}\right)>\mathrm{0} \\ $$
Commented by Joel578 last updated on 07/Apr/20
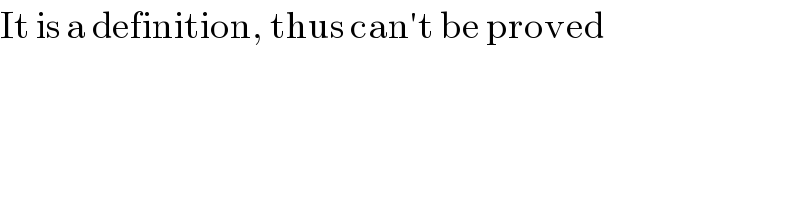
It is a definition, thus can′t be proved
$$\mathrm{It}\:\mathrm{is}\:\mathrm{a}\:\mathrm{definition},\:\mathrm{thus}\:\mathrm{can}'\mathrm{t}\:\mathrm{be}\:\mathrm{proved} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *