Question Number 19351 by Tinkutara last updated on 10/Aug/17
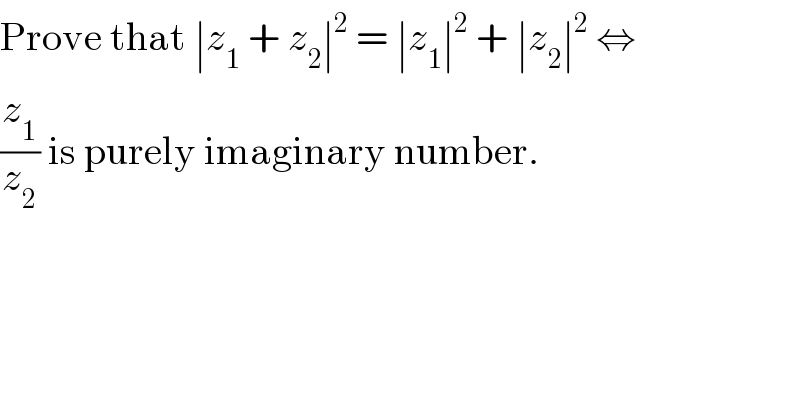
$$\mathrm{Prove}\:\mathrm{that}\:\mid{z}_{\mathrm{1}} \:+\:{z}_{\mathrm{2}} \mid^{\mathrm{2}} \:=\:\mid{z}_{\mathrm{1}} \mid^{\mathrm{2}} \:+\:\mid{z}_{\mathrm{2}} \mid^{\mathrm{2}} \:\Leftrightarrow \\ $$$$\frac{{z}_{\mathrm{1}} }{{z}_{\mathrm{2}} }\:\mathrm{is}\:\mathrm{purely}\:\mathrm{imaginary}\:\mathrm{number}. \\ $$
Commented by dioph last updated on 10/Aug/17
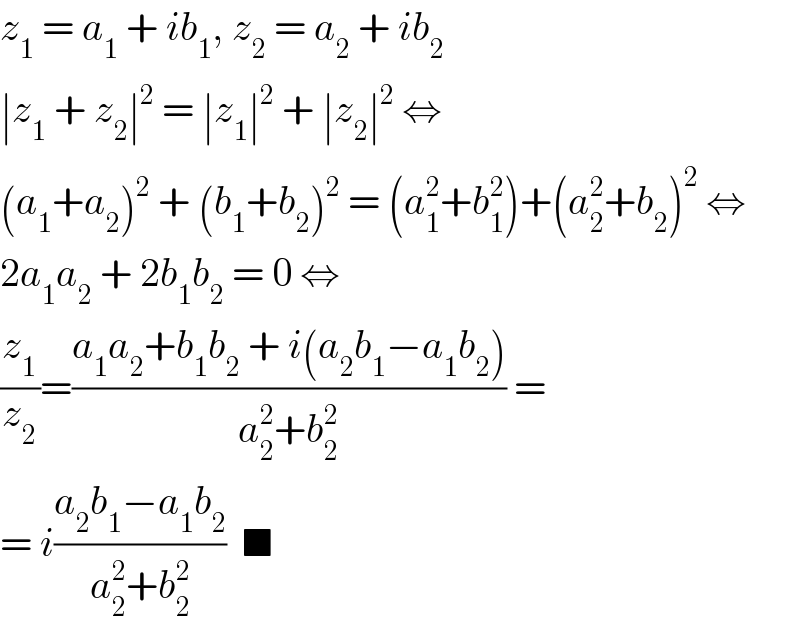
$${z}_{\mathrm{1}} \:=\:{a}_{\mathrm{1}} \:+\:{ib}_{\mathrm{1}} ,\:{z}_{\mathrm{2}} \:=\:{a}_{\mathrm{2}} \:+\:{ib}_{\mathrm{2}} \\ $$$$\mid{z}_{\mathrm{1}} \:+\:{z}_{\mathrm{2}} \mid^{\mathrm{2}} \:=\:\mid{z}_{\mathrm{1}} \mid^{\mathrm{2}} \:+\:\mid{z}_{\mathrm{2}} \mid^{\mathrm{2}} \:\Leftrightarrow \\ $$$$\left({a}_{\mathrm{1}} +{a}_{\mathrm{2}} \right)^{\mathrm{2}} \:+\:\left({b}_{\mathrm{1}} +{b}_{\mathrm{2}} \right)^{\mathrm{2}} \:=\:\left({a}_{\mathrm{1}} ^{\mathrm{2}} +{b}_{\mathrm{1}} ^{\mathrm{2}} \right)+\left({a}_{\mathrm{2}} ^{\mathrm{2}} +{b}_{\mathrm{2}} \right)^{\mathrm{2}} \:\Leftrightarrow \\ $$$$\mathrm{2}{a}_{\mathrm{1}} {a}_{\mathrm{2}} \:+\:\mathrm{2}{b}_{\mathrm{1}} {b}_{\mathrm{2}} \:=\:\mathrm{0}\:\Leftrightarrow \\ $$$$\frac{{z}_{\mathrm{1}} }{{z}_{\mathrm{2}} }=\frac{{a}_{\mathrm{1}} {a}_{\mathrm{2}} +{b}_{\mathrm{1}} {b}_{\mathrm{2}} \:+\:{i}\left({a}_{\mathrm{2}} {b}_{\mathrm{1}} −{a}_{\mathrm{1}} {b}_{\mathrm{2}} \right)}{{a}_{\mathrm{2}} ^{\mathrm{2}} +{b}_{\mathrm{2}} ^{\mathrm{2}} }\:= \\ $$$$=\:{i}\frac{{a}_{\mathrm{2}} {b}_{\mathrm{1}} −{a}_{\mathrm{1}} {b}_{\mathrm{2}} }{{a}_{\mathrm{2}} ^{\mathrm{2}} +{b}_{\mathrm{2}} ^{\mathrm{2}} }\:\:\blacksquare \\ $$
Commented by Tinkutara last updated on 10/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
Answered by ajfour last updated on 10/Aug/17
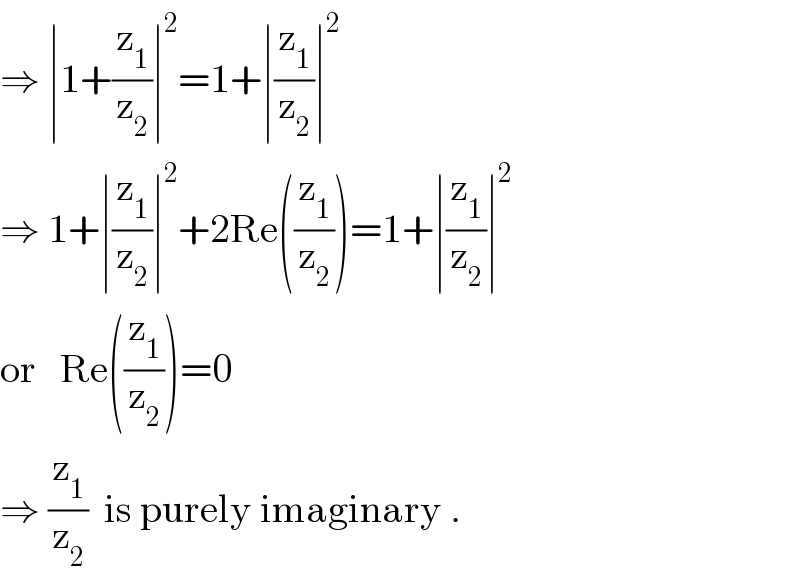
$$\Rightarrow\:\mid\mathrm{1}+\frac{\mathrm{z}_{\mathrm{1}} }{\mathrm{z}_{\mathrm{2}} }\mid^{\mathrm{2}} =\mathrm{1}+\mid\frac{\mathrm{z}_{\mathrm{1}} }{\mathrm{z}_{\mathrm{2}} }\mid^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{1}+\mid\frac{\mathrm{z}_{\mathrm{1}} }{\mathrm{z}_{\mathrm{2}} }\mid^{\mathrm{2}} +\mathrm{2Re}\left(\frac{\mathrm{z}_{\mathrm{1}} }{\mathrm{z}_{\mathrm{2}} }\right)=\mathrm{1}+\mid\frac{\mathrm{z}_{\mathrm{1}} }{\mathrm{z}_{\mathrm{2}} }\mid^{\mathrm{2}} \\ $$$$\mathrm{or}\:\:\:\mathrm{Re}\left(\frac{\mathrm{z}_{\mathrm{1}} }{\mathrm{z}_{\mathrm{2}} }\right)=\mathrm{0}\:\: \\ $$$$\Rightarrow\:\frac{\mathrm{z}_{\mathrm{1}} }{\mathrm{z}_{\mathrm{2}} }\:\:\mathrm{is}\:\mathrm{purely}\:\mathrm{imaginary}\:. \\ $$
Commented by Tinkutara last updated on 10/Aug/17
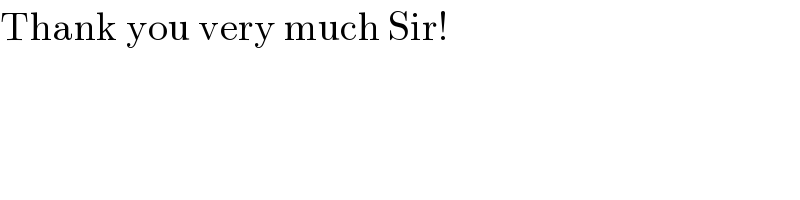
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
