Question Number 127400 by mohammad17 last updated on 29/Dec/20
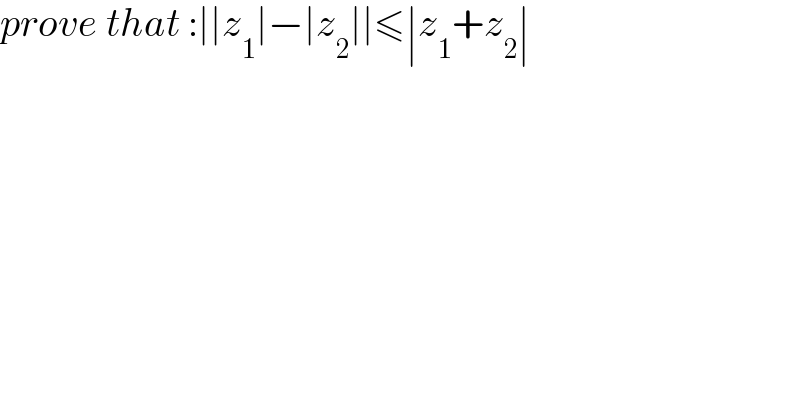
$${prove}\:{that}\::\mid\mid{z}_{\mathrm{1}} \mid−\mid{z}_{\mathrm{2}} \mid\mid\leqslant\mid{z}_{\mathrm{1}} +{z}_{\mathrm{2}} \mid \\ $$
Commented by mohammad17 last updated on 29/Dec/20

$$? \\ $$
Commented by liberty last updated on 29/Dec/20
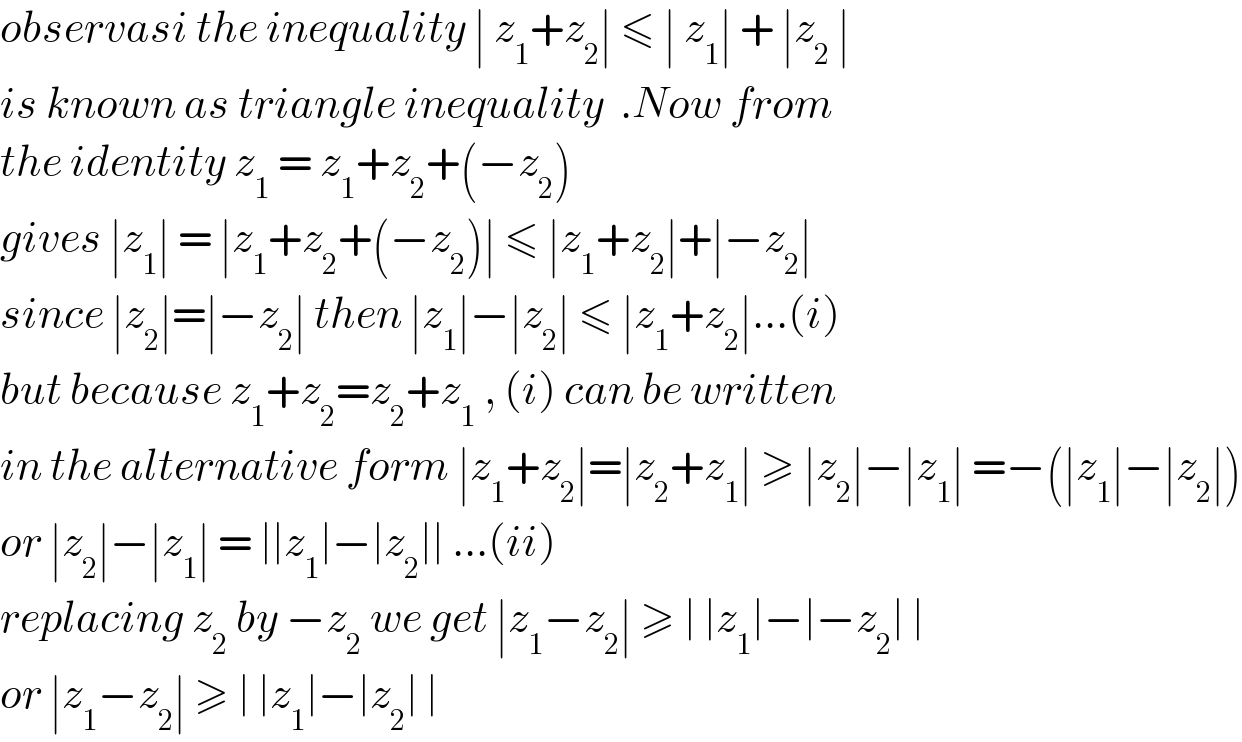
$${observasi}\:{the}\:{inequality}\:\mid\:{z}_{\mathrm{1}} +{z}_{\mathrm{2}} \mid\:\leqslant\:\mid\:{z}_{\mathrm{1}} \mid\:+\:\mid{z}_{\mathrm{2}} \:\mid \\ $$$${is}\:{known}\:{as}\:{triangle}\:{inequality}\:\:.{Now}\:{from} \\ $$$${the}\:{identity}\:{z}_{\mathrm{1}} \:=\:{z}_{\mathrm{1}} +{z}_{\mathrm{2}} +\left(−{z}_{\mathrm{2}} \right) \\ $$$${gives}\:\mid{z}_{\mathrm{1}} \mid\:=\:\mid{z}_{\mathrm{1}} +{z}_{\mathrm{2}} +\left(−{z}_{\mathrm{2}} \right)\mid\:\leqslant\:\mid{z}_{\mathrm{1}} +{z}_{\mathrm{2}} \mid+\mid−{z}_{\mathrm{2}} \mid \\ $$$${since}\:\mid{z}_{\mathrm{2}} \mid=\mid−{z}_{\mathrm{2}} \mid\:{then}\:\mid{z}_{\mathrm{1}} \mid−\mid{z}_{\mathrm{2}} \mid\:\leqslant\:\mid{z}_{\mathrm{1}} +{z}_{\mathrm{2}} \mid…\left({i}\right) \\ $$$${but}\:{because}\:{z}_{\mathrm{1}} +{z}_{\mathrm{2}} ={z}_{\mathrm{2}} +{z}_{\mathrm{1}} \:,\:\left({i}\right)\:{can}\:{be}\:{written}\: \\ $$$${in}\:{the}\:{alternative}\:{form}\:\mid{z}_{\mathrm{1}} +{z}_{\mathrm{2}} \mid=\mid{z}_{\mathrm{2}} +{z}_{\mathrm{1}} \mid\:\geqslant\:\mid{z}_{\mathrm{2}} \mid−\mid{z}_{\mathrm{1}} \mid\:=−\left(\mid{z}_{\mathrm{1}} \mid−\mid{z}_{\mathrm{2}} \mid\right) \\ $$$${or}\:\mid{z}_{\mathrm{2}} \mid−\mid{z}_{\mathrm{1}} \mid\:=\:\mid\mid{z}_{\mathrm{1}} \mid−\mid{z}_{\mathrm{2}} \mid\mid\:…\left({ii}\right) \\ $$$${replacing}\:{z}_{\mathrm{2}} \:{by}\:−{z}_{\mathrm{2}} \:{we}\:{get}\:\mid{z}_{\mathrm{1}} −{z}_{\mathrm{2}} \mid\:\geqslant\:\mid\:\mid{z}_{\mathrm{1}} \mid−\mid−{z}_{\mathrm{2}} \mid\:\mid \\ $$$${or}\:\mid{z}_{\mathrm{1}} −{z}_{\mathrm{2}} \mid\:\geqslant\:\mid\:\mid{z}_{\mathrm{1}} \mid−\mid{z}_{\mathrm{2}} \mid\:\mid \\ $$
