prove-the-compact-form-of-multivariable-Taylor-series-T-B-n-1-n-2-n-d-0-i-0-n-d-x-i-d-i-i-0-n-d-n-i-i-0-n-d-x-i-f-

Question Number 98116 by M±th+et+s last updated on 11/Jun/20

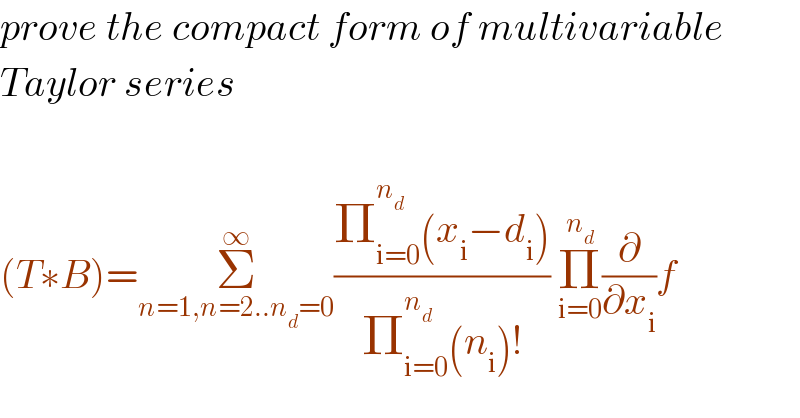
p r o v e t h e c o m p a c t f o r m o f m u l t i v a r i a b l e

T a y l o r s e r i e s

(T * B) = \underset{n = 1, n = 2 . . n_{d} = 0}{\sum^{\infty}} \frac{\prod_{i = 0}^{n_{d}} (x_{i} - d_{i})}{\prod_{i = 0}^{n_{d}} (n_{i})!} \underset{i = 0}{\prod^{n_{d}}} \frac{\partial}{\partial x_{i}} f