Question Number 122624 by Ar Brandon last updated on 18/Nov/20
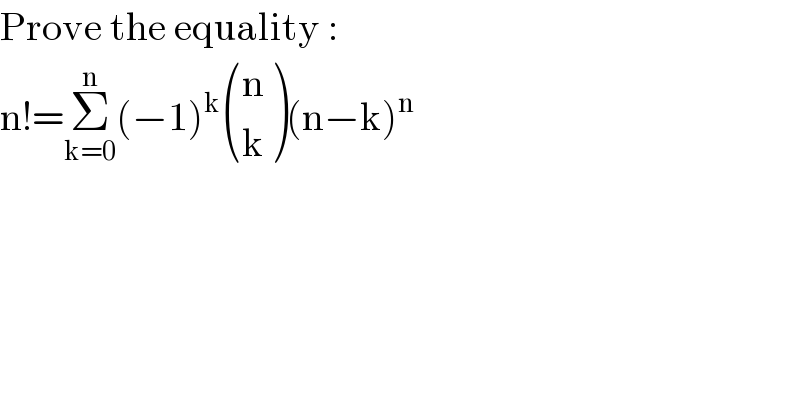
$$\mathrm{Prove}\:\mathrm{the}\:\mathrm{equality}\:: \\ $$$$\mathrm{n}!=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{k}} \begin{pmatrix}{\mathrm{n}}\\{\mathrm{k}}\end{pmatrix}\left(\mathrm{n}−\mathrm{k}\right)^{\mathrm{n}} \\ $$
Answered by mindispower last updated on 18/Nov/20
![let f(x,y)=e^y (e^y −x)^n f(x,y)=e^y [Σ_(k=0) ^n (−x)^k C_k ^n e^((n−k)y) ] =Σ_(k=0) ^n e^((n+1−k)y) (−1)^k x^k C_k ^n f(1,y)=Σ_(k=0) ^n e^((n+1−k)y) (−1)^k C_n ^k let∂_y ^k f(1,y) bee k derivate f over y we want ∂_y ^n f(1,0) ∂_y ^n f(1,y)=Σ_(k≤n) (n+1−k)^n e^((n+1−k)y) (−1)^k C_n ^k ∂_y ^n f(1,0)=Σ_(k≤n) (n+1−k)^n (−1)^k C_n ^k f(1,y)=e^y (e^y −1)^n =e^y (e^(y/2) (e^(y/2) −e^(−(y/2)) ))^n =e^((1+(n/2))y) 2^n sh^n ((y/2))=g((y/2))=f(1,y) let (y/2)=z g(z)=h(y),(∂h/∂y)=(∂h/∂z).(∂z/∂y)=(∂g/∂z) .(1/2) ⇒∂^n h(y)=(1/2^n ).(∂^n g/∂z^n ) ⇒∂_y ^n f(1,y)∣_(y=0) =∂_z ^n e^((2+n)z) sh^n (z)∣_(z=0) we show that ∀k<n ∂_x ^k sh^n (x)∣_(x=0) =0..E ∂_x sh^n (x)=nch(x)sh^(n−1) (x) we know sh(0)=0 all sh^i (x)∣x=0 give zero only i=0 but derivate k<n the least power of sh is n−k≥1 ⇒ we have all power of sh^m (x),m∈[n−k,n] =0 ⇒∂_z ^n e^(2+n) sh^n (z)=ΣC_n ^k (e^((2+n)z) )^((n−k)) sh^n (z)^((k)) by proposition?E? we now that the only facteur we want isC_n ^n e^((2+n)z) (sh^n (z))^((n)) ∣_(z=0) sh^n (z)^((n)) =(nch(z)sh^(n−1) (z))^(n−1) ..apply E againe we want nch(z)(sh^(n−1) (z))^(n−1) =n(ch(z)(n−1)ch(z)(sh^(n−2) (z))^(n−2) ..... =n(n−1)(n−2)........(n−(n−1))(sh^(n−(n−1) (z))^((n−(n−1))) =(n)!.(sh(z))^′ ∣_(z=0) =n!ch(0)=n!](https://www.tinkutara.com/question/Q122656.png)
$${let}\:{f}\left({x},{y}\right)={e}^{{y}} \left({e}^{{y}} −{x}\right)^{{n}} \\ $$$${f}\left({x},{y}\right)={e}^{{y}} \left[\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left(−{x}\right)^{{k}} {C}_{{k}} ^{{n}} {e}^{\left({n}−{k}\right){y}} \right] \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{e}^{\left({n}+\mathrm{1}−{k}\right){y}} \left(−\mathrm{1}\right)^{{k}} {x}^{{k}} {C}_{{k}} ^{{n}} \\ $$$${f}\left(\mathrm{1},{y}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{e}^{\left({n}+\mathrm{1}−{k}\right){y}} \left(−\mathrm{1}\right)^{{k}} {C}_{{n}} ^{{k}} \\ $$$${let}\partial_{{y}} ^{{k}} {f}\left(\mathrm{1},{y}\right)\:{bee}\:{k}\:{derivate}\:{f}\:{over}\:{y} \\ $$$${we}\:{want}\:\partial_{{y}} ^{{n}} {f}\left(\mathrm{1},\mathrm{0}\right) \\ $$$$\partial_{{y}} ^{{n}} {f}\left(\mathrm{1},{y}\right)=\underset{{k}\leqslant{n}} {\sum}\left({n}+\mathrm{1}−{k}\right)^{{n}} {e}^{\left({n}+\mathrm{1}−{k}\right){y}} \left(−\mathrm{1}\right)^{{k}} {C}_{{n}} ^{{k}} \\ $$$$\partial_{{y}} ^{{n}} {f}\left(\mathrm{1},\mathrm{0}\right)=\underset{{k}\leqslant{n}} {\sum}\left({n}+\mathrm{1}−{k}\right)^{{n}} \left(−\mathrm{1}\right)^{{k}} {C}_{{n}} ^{{k}} \\ $$$${f}\left(\mathrm{1},{y}\right)={e}^{{y}} \left({e}^{{y}} −\mathrm{1}\right)^{{n}} \\ $$$$={e}^{{y}} \left({e}^{\frac{{y}}{\mathrm{2}}} \left({e}^{\frac{{y}}{\mathrm{2}}} −{e}^{−\frac{{y}}{\mathrm{2}}} \right)\right)^{{n}} \\ $$$$={e}^{\left(\mathrm{1}+\frac{{n}}{\mathrm{2}}\right){y}} \mathrm{2}^{{n}} {sh}^{{n}} \left(\frac{{y}}{\mathrm{2}}\right)={g}\left(\frac{{y}}{\mathrm{2}}\right)={f}\left(\mathrm{1},{y}\right) \\ $$$${let}\:\frac{{y}}{\mathrm{2}}={z} \\ $$$${g}\left({z}\right)={h}\left({y}\right),\frac{\partial{h}}{\partial{y}}=\frac{\partial{h}}{\partial{z}}.\frac{\partial{z}}{\partial{y}}=\frac{\partial{g}}{\partial{z}}\:\:.\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\partial^{{n}} {h}\left({y}\right)=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }.\frac{\partial^{{n}} {g}}{\partial{z}^{{n}} } \\ $$$$\Rightarrow\partial_{{y}} ^{{n}} {f}\left(\mathrm{1},{y}\right)\mid_{{y}=\mathrm{0}} =\partial_{{z}} ^{{n}} {e}^{\left(\mathrm{2}+{n}\right){z}} {sh}^{{n}} \left({z}\right)\mid_{{z}=\mathrm{0}} \\ $$$${we}\:{show}\:{that}\:\forall{k}<{n}\:\:\partial_{{x}} ^{{k}} {sh}^{{n}} \left({x}\right)\mid_{{x}=\mathrm{0}} =\mathrm{0}..{E} \\ $$$$\partial_{{x}} {sh}^{{n}} \left({x}\right)={nch}\left({x}\right){sh}^{{n}−\mathrm{1}} \left({x}\right) \\ $$$${we}\:{know}\:{sh}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${all}\:{sh}^{{i}} \left({x}\right)\mid{x}=\mathrm{0}\:{give}\:{zero}\:{only}\:{i}=\mathrm{0} \\ $$$${but}\:{derivate}\:{k}<{n}\:{the}\:{least}\:{power}\:{of}\:{sh}\:{is}\:{n}−{k}\geqslant\mathrm{1} \\ $$$$\Rightarrow\:{we}\:{have}\:{all}\:{power}\:{of}\:{sh}^{{m}} \left({x}\right),{m}\in\left[{n}−{k},{n}\right] \\ $$$$=\mathrm{0} \\ $$$$\Rightarrow\partial_{{z}} ^{{n}} {e}^{\mathrm{2}+{n}} {sh}^{{n}} \left({z}\right)=\Sigma{C}_{{n}} ^{{k}} \left({e}^{\left(\mathrm{2}+{n}\right){z}} \:\:\right)^{\left({n}−{k}\right)} {sh}^{{n}} \left({z}\right)^{\left({k}\right)} \\ $$$${by}\:{proposition}?{E}? \\ $$$${we}\:{now}\:{that} \\ $$$${the}\:{only}\:{facteur}\:{we}\:{want} \\ $$$${isC}_{{n}} ^{{n}} {e}^{\left(\mathrm{2}+{n}\right){z}} \left({sh}^{{n}} \left({z}\right)\right)^{\left({n}\right)} \mid_{{z}=\mathrm{0}} \\ $$$${sh}^{{n}} \left({z}\right)^{\left({n}\right)} =\left({nch}\left({z}\right){sh}^{{n}−\mathrm{1}} \left({z}\right)\right)^{{n}−\mathrm{1}} ..{apply}\:{E}\:{againe} \\ $$$${we}\:{want}\:{nch}\left({z}\right)\left({sh}^{{n}−\mathrm{1}} \left({z}\right)\right)^{{n}−\mathrm{1}} \\ $$$$={n}\left({ch}\left({z}\right)\left({n}−\mathrm{1}\right){ch}\left({z}\right)\left({sh}^{{n}−\mathrm{2}} \left({z}\right)\right)^{{n}−\mathrm{2}} …..\right. \\ $$$$={n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)……..\left({n}−\left({n}−\mathrm{1}\right)\right)\left({sh}^{{n}−\left({n}−\mathrm{1}\right.} \left({z}\right)\right)^{\left({n}−\left({n}−\mathrm{1}\right)\right)} \\ $$$$=\left({n}\right)!.\left({sh}\left({z}\right)\right)^{'} \mid_{{z}=\mathrm{0}} \\ $$$$={n}!{ch}\left(\mathrm{0}\right)={n}! \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
