Question Number 119246 by 1549442205PVT last updated on 23/Oct/20

$$\mathrm{Prove}\:\mathrm{the}\:\mathrm{following}\:\:\mathrm{inequalities}\:\mathrm{hold} \\ $$$$\:\:\mathrm{true}\:\forall\mathrm{x}\in\mathrm{R} \\ $$$$\left.\mathrm{a}\right)\mathrm{cos}\left(\mathrm{cosx}\right)>\mathrm{0} \\ $$$$\left.\mathrm{b}\right)\mathrm{cos}\left(\mathrm{sinx}\right)>\mathrm{sin}\left(\mathrm{cosx}\right) \\ $$
Answered by Olaf last updated on 23/Oct/20
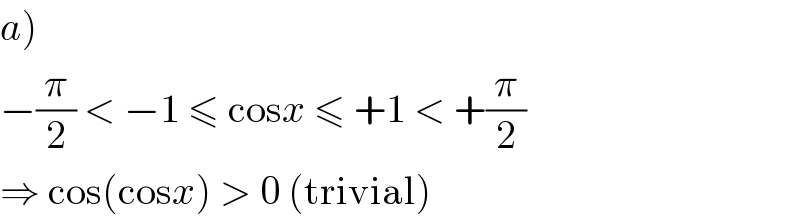
$$\left.{a}\right) \\ $$$$−\frac{\pi}{\mathrm{2}}\:<\:−\mathrm{1}\:\leqslant\:\mathrm{cos}{x}\:\leqslant\:+\mathrm{1}\:<\:+\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{cos}\left(\mathrm{cos}{x}\right)\:>\:\mathrm{0}\:\left(\mathrm{trivial}\right) \\ $$
Answered by mindispower last updated on 23/Oct/20
![cos(sin(x))>0,∀x∈R sin(cos(x))<0,∀x∈[−π,−(π/2)]∪[(π/2),π] so we worck just in [−(π/2),(π/2)] x→cos(sin(−x))=cos(sin(−x)) sin(cos(−x))=sin(cos(x))⇒ just x∈[0,(π/2)] lets[solve in x∈[0,(π/2)] cos(sin(x))>sin(cos(x)) ⇔ sin((π/2)−sin(x))>sin(cos(x)) since cos(x),(π/2)−sin(x)∈[0,(π/2)] and sin increase function ⇔(π/2)−sin(x)>cos(x) ⇔sin(x)+cos(x)<(π/2)...E ∣sin(x)+cos(x)∣≤(√(1^2 +1^2 )).(√(cos^2 (x)+sin^2 ))=(√2)<(π/2) cauchy shwartz.. by equivalent E true ⇒sin((π/2)−sin(x))>sin(cos(x)) ⇔cos(sin(x))>sin(cos(x))](https://www.tinkutara.com/question/Q119328.png)
$${cos}\left({sin}\left({x}\right)\right)>\mathrm{0},\forall{x}\in\mathbb{R} \\ $$$${sin}\left({cos}\left({x}\right)\right)<\mathrm{0},\forall{x}\in\left[−\pi,−\frac{\pi}{\mathrm{2}}\right]\cup\left[\frac{\pi}{\mathrm{2}},\pi\right] \\ $$$${so}\:{we}\:{worck}\:{just}\:{in}\:\left[−\frac{\pi}{\mathrm{2}},\frac{\pi}{\mathrm{2}}\right] \\ $$$${x}\rightarrow{cos}\left({sin}\left(−{x}\right)\right)={cos}\left({sin}\left(−{x}\right)\right) \\ $$$${sin}\left({cos}\left(−{x}\right)\right)={sin}\left({cos}\left({x}\right)\right)\Rightarrow \\ $$$${just}\:{x}\in\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\right] \\ $$$${lets}\left[{solve}\:{in}\:{x}\in\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\right]\right. \\ $$$${cos}\left({sin}\left({x}\right)\right)>{sin}\left({cos}\left({x}\right)\right) \\ $$$$\Leftrightarrow \\ $$$${sin}\left(\frac{\pi}{\mathrm{2}}−{sin}\left({x}\right)\right)>{sin}\left({cos}\left({x}\right)\right) \\ $$$${since}\:{cos}\left({x}\right),\frac{\pi}{\mathrm{2}}−{sin}\left({x}\right)\in\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\right]\:{and}\:{sin}\:{increase} \\ $$$${function} \\ $$$$\Leftrightarrow\frac{\pi}{\mathrm{2}}−{sin}\left({x}\right)>{cos}\left({x}\right) \\ $$$$\Leftrightarrow{sin}\left({x}\right)+{cos}\left({x}\right)<\frac{\pi}{\mathrm{2}}…{E} \\ $$$$\mid{sin}\left({x}\right)+{cos}\left({x}\right)\mid\leqslant\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }.\sqrt{{cos}^{\mathrm{2}} \left({x}\right)+{sin}^{\mathrm{2}} }=\sqrt{\mathrm{2}}<\frac{\pi}{\mathrm{2}} \\ $$$${cauchy}\:{shwartz}.. \\ $$$${by}\:{equivalent}\:{E}\:{true} \\ $$$$\Rightarrow{sin}\left(\frac{\pi}{\mathrm{2}}−{sin}\left({x}\right)\right)>{sin}\left({cos}\left({x}\right)\right) \\ $$$$\Leftrightarrow{cos}\left({sin}\left({x}\right)\right)>{sin}\left({cos}\left({x}\right)\right) \\ $$$$ \\ $$
