Question Number 158301 by LEKOUMA last updated on 02/Nov/21
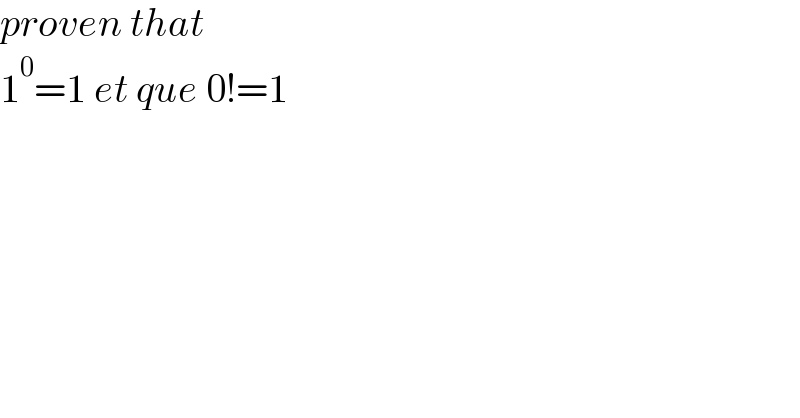
$${proven}\:{that}\: \\ $$$$\mathrm{1}^{\mathrm{0}} =\mathrm{1}\:{et}\:{que}\:\mathrm{0}!=\mathrm{1} \\ $$
Commented by Rasheed.Sindhi last updated on 02/Nov/21
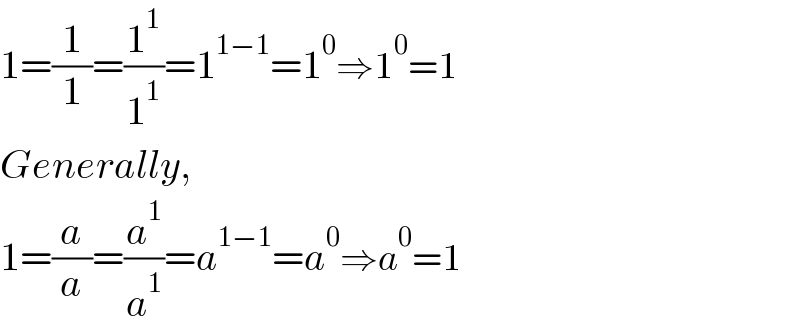
$$\mathrm{1}=\frac{\mathrm{1}}{\mathrm{1}}=\frac{\mathrm{1}^{\mathrm{1}} }{\mathrm{1}^{\mathrm{1}} }=\mathrm{1}^{\mathrm{1}−\mathrm{1}} =\mathrm{1}^{\mathrm{0}} \Rightarrow\mathrm{1}^{\mathrm{0}} =\mathrm{1} \\ $$$${Generally}, \\ $$$$\mathrm{1}=\frac{{a}}{{a}}=\frac{{a}^{\mathrm{1}} }{{a}^{\mathrm{1}} }={a}^{\mathrm{1}−\mathrm{1}} ={a}^{\mathrm{0}} \Rightarrow{a}^{\mathrm{0}} =\mathrm{1} \\ $$
Answered by physicstutes last updated on 02/Nov/21
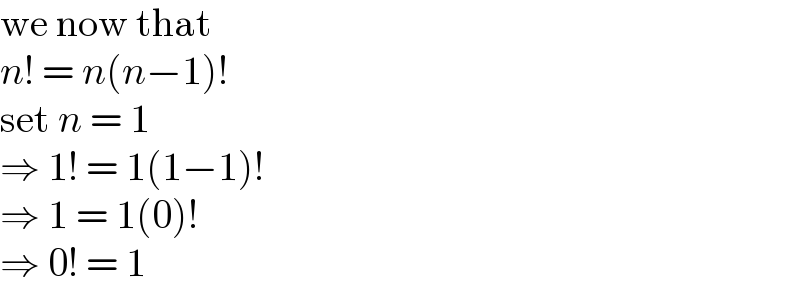
$$\mathrm{we}\:\mathrm{now}\:\mathrm{that} \\ $$$${n}!\:=\:{n}\left({n}−\mathrm{1}\right)! \\ $$$$\mathrm{set}\:{n}\:=\:\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{1}!\:=\:\mathrm{1}\left(\mathrm{1}−\mathrm{1}\right)! \\ $$$$\Rightarrow\:\mathrm{1}\:=\:\mathrm{1}\left(\mathrm{0}\right)! \\ $$$$\Rightarrow\:\mathrm{0}!\:=\:\mathrm{1} \\ $$
