Question Number 34675 by math khazana by abdo last updated on 09/May/18
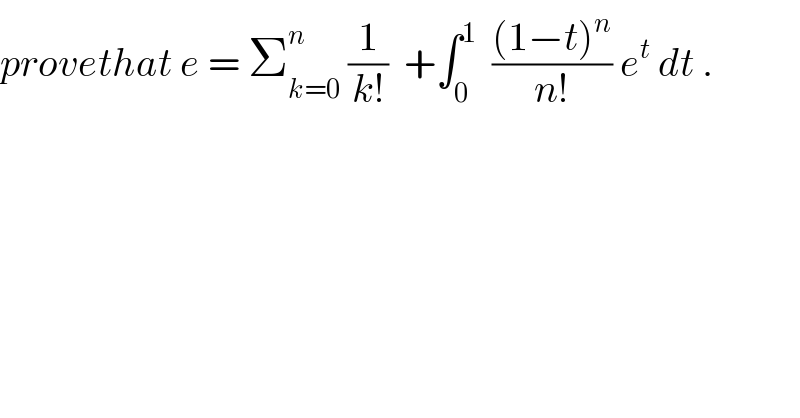
$${provethat}\:{e}\:=\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{{k}!}\:\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\left(\mathrm{1}−{t}\right)^{{n}} }{{n}!}\:{e}^{{t}} \:{dt}\:. \\ $$
