Q-13724-Reposted-E-xpansion-of-1000-has-24-0-s-at-the-end-Find-the-first-non-zero-digit-from-right-1000-d0000-0-What-is-the-the-value-of-d-

Question Number 15543 by RasheedSoomro last updated on 11/Jun/17

You can't use 'macro parameter character #' in math mode

E_{}^{} xpansion of 1000!

has 24 0^{'} s at the end . Find

the first non - zero digit

from right .

1000! = \dots . d 0000 \dots 0

What is the the value of d ?

Answered by RasheedSoomro last updated on 11/Jun/17

Used results :

(5 k + 1) (5 k + 2) (5 k + 3) (5 k + 4) \equiv 4 (\mod 10)

\frac{(5 k + 1) (5 k + 2) (5 k + 3) (5 k + 4)}{2} \equiv 2 (\mod 10)

- - - - - - - - - - - - - - - - - - - - - - - - - - - - -

E xpansion of 1000! has 249 0^{'} s at the end .

Let p = \frac{1000!}{10^{249}}, p has no 0 at the end .

p = \frac{1000!}{2^{249} \times 5^{249}}

We can write

5^{249} = 5 \times \frac{10}{2} \times \frac{15}{3} \times \dots \frac{965}{193} \times \dots \frac{985}{197} \times \frac{990}{2 . 3^{2} . 11} \times . \frac{995}{199} \times \frac{1000}{2^{3}}

= \frac{5.10.15 \dots . 1000}{2^{α_{2}} \times 3^{α_{3}} \times 7^{α_{7}} \times \dots 193^{α_{193}} \times 197^{α_{197}} \times 199^{α_{199}}}

α_{2} = ⌊ \frac{1000}{10} ⌋ + ⌊ \frac{1000}{20} ⌋ + ⌊ \frac{1000}{40} ⌋ + ⌊ \frac{1000}{80} ⌋ + ⌊ \frac{1000}{160} ⌋ + ⌊ \frac{1000}{320} ⌋ + ⌊ \frac{1000}{640} ⌋

= 100 + 50 + 25 + 12 + 6 + 3 + 1 = 197

α_{3} = ⌊ \frac{1000}{15} ⌋ + ⌊ \frac{1000}{45} ⌋ + ⌊ \frac{1000}{135} ⌋ + ⌊ \frac{1000}{405} ⌋ = 66 + 22 + 7 + 2 = 97

By same formula

α_{7} = 32, α_{11} = 19, α_{13} = 16, α_{17} = 11, α_{19} = 10, α_{23} = 8,

α_{29} = α_{31} = 6, α_{37} = 5, α_{41} = α_{43} = α_{47} = 4, α_{53} = α_{59} = α_{61} = 3,

α_{67} = α_{71} = α_{73} = α_{79} = α_{83} = α_{89} = α_{97} = 2

α_{101} = α_{103} = \dots = α_{199} = 1

Hence

5^{249} = \frac{5.10.15 \dots . 1000}{2^{197} . 3^{97} . 7^{32} \dots 199^{1}}

So

p = \frac{1000!}{2^{249} \times 5^{249}} = \frac{1000!}{2^{249} \times (\frac{5.10.15 \dots . 1000}{2^{197} . 3^{97} . 7^{32} \dots 199^{1}})}

p = \frac{1000!}{2^{249} \times 5^{249}} = \frac{1000!}{2^{52} \times (\frac{5.10.15 \dots . 1000}{3^{97} . 7^{32} \dots 199^{1}})}

p = (3^{97} . 7^{32} \dots 199^{1}) (\frac{1000!}{2^{52} (5.10 \dots 1000})

p = (3^{97} . 7^{32} \dots 199^{1}) {(\frac{1.2.3.4}{2}) (6 \dots 9) (11 \dots . 14) (\frac{16 \dots 19}{2})}

\times {(21 \dots 24) (26 \dots . 29) (31 \dots 34) (\frac{36 \dots 39}{2})}

\times \dots \times {(981 \dots 984) (986 \dots 989) (991 \dots 994) (\frac{996 \dots 999}{2})}

Now we can see that

3^{97} \equiv 3, 7^{32} \equiv 1, 11^{19} \equiv 1, 13^{16} \equiv 1, 17^{11} \equiv 3, 19^{10} \equiv 1, 23^{8} \equiv 1

Continue

Commented by tawa tawa last updated on 11/Jun/17

Weldone sir .

Commented by RasheedSoomro last updated on 12/Jun/17

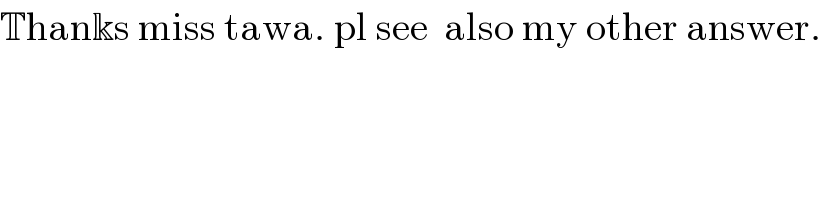
T han k s miss tawa . pl see also my other answer .

Answered by RasheedSoomro last updated on 12/Jun/17

\underline{NEW APPROACH} (The simplest approach)

Used results

(5 k + 1) (5 k + 2) (5 k + 3) (5 k + 4) \equiv 4 (\mod 10)

\frac{(5 k + 1) (5 k + 2) (5 k + 3) (5 k + 4)}{2} \equiv 2 (\mod 10)

2^{4 k + 1} \equiv 2 (\mod 10)

4^{2 k} \equiv 6 (\mod 10)

- - - - - - - - - - - - - - - - - - - - - - - -

E xpansion of 1000! has 249 0^{'} s at the end

p = \frac{1000!}{10^{249}} has no zero at the end .

Let f (n) = n!

f (1000) = 1000! = (1 \dots 4) (5 \dots 9) \dots (996 \dots 999) (5.10.15 \dots 1000)

= (1 \dots 4) (6 \dots 9) \dots (996 \dots 999) . 5^{200} . (1.2.3 \dots 200)

= 5^{200} (1 \dots 4) (6 \dots 9) \dots (996 \dots 999) \times f (200)

f (200) = (1 \dots 4) (6 \dots 9) \dots (196 \dots l 99) (5.10 \dots 200)

= 5^{40} (1 \dots 4) (6 \dots 9) \dots (196 \dots l 99) (1.2 \dots 40)

= 5^{40} (1 \dots 4) (6 \dots 9) \dots (196 \dots l 99) \times f (40)

f (40) = (1 \dots 4) (6 \dots 9) \dots (36 \dots 39) (5.10 \dots 40)

= 5^{8} (1 \dots 4) (6 \dots 9) \dots (36 \dots 39) (1.2 \dots 8)

= 5^{8} (1 \dots 4) (6 \dots 9) \dots (36 \dots 39) \times f (8)

f (8) = (1.2.3.4) (5.6.7.8) (5)

= 5 (1.2.3.4) (6.7.8)

f (1000) = 5^{200} (1 \dots 4) (6 \dots 9) \dots (996 \dots 999)

\times 5^{40} (1 \dots 4) (6 \dots 9) \dots (196 \dots l 99)

\times 5^{8} (1 \dots 4) (6 \dots 9) \dots (36 \dots 39)

\times 5 (1 \dots 4) (6.7.8)

= 5^{249} {(1 \dots 4)}^{4} {(6 \dots 9)}^{3} (6.7.8) \dots {(36 \dots 39)}^{3}

\times {(41 \dots 44)}^{2} \dots {(196 \dots 199)}^{2}

\times (201 \dots 204) \dots (996 \dots 999)

p = \frac{f (1000)}{2^{249} . 5^{249}}

= (\frac{1}{2^{249}}) (6.7.8) {(1 \dots 4)}^{4} {(6 \dots 9)}^{3} {(11 \dots 14)}^{3} \dots {(36 \dots 39)}^{3}

\times {(41 \dots 44)}^{2} {(46 \dots 49)}^{2} \dots {(196 \dots 199)}^{2}

\times (201 \dots 204) \dots (996 \dots 999)

= {(1 \dots 4) (6 \dots 9) \dots (996 \dots 999)}

= (6.7.8) (

= (\frac{1}{2^{249}}) {\overset{8 brackets}{(1 \dots 4) \dots (36 \dots . 39)}}^{3}

\times {\overset{32 brackets}{(41 \dots 44) \dots (196 \dots 199)}}^{2}

\times {\overset{180 brackets}{(201 \dots 204) \dots (996 \dots 999)}}

\times {(1 \dots 4) (6.7.8}

Total number of brackets = 8 \times 3 + 32 \times 2 + 180 + 2 = 270

Any of 249 brackets could be given 2 as denominator

(\frac{* . * . * . *}{2}) \equiv 2 (\mod 10) [249 congruences]

(* . * . * . *) \equiv 4 (\mod 10) [20 congruences]

6.7.8 \equiv 6 (\mod 10) [1 congruence]

Multiplying above congruences

p \equiv 2^{249 ∙} . 4^{20 *} . 6 (\mod 2)

\equiv 2.6.6 (\mod 10)

\equiv 2 (\mod 10

Commented by mrW1 last updated on 12/Jun/17

I appreciate very that you never stop

before the solution is found!

Commented by tawa tawa last updated on 12/Jun/17

Wow, kudox sir .

Commented by mrW1 last updated on 12/Jun/17

C ONGRATULATION SIR!

Commented by RasheedSoomro last updated on 12/Jun/17

TH α n k s SIR!

A p a r t o f y o u r c o n g r a t u l a t i o n

r e t u r n s t o y o u, b e c a u s e i t i s

b a s e d o n a r e s u l t p r o v e d b y y o u!

Commented by mrW1 last updated on 12/Jun/17

Can you find the last non - zero digit

of 2000! using your method ?

Commented by RasheedSoomro last updated on 12/Jun/17

I think I can sir .