Question Number 173411 by mnjuly1970 last updated on 11/Jul/22
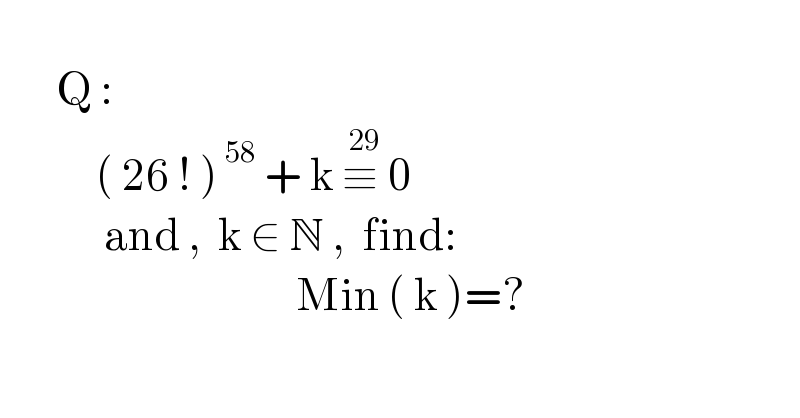
$$ \\ $$$$\:\:\:\:\:\:\:\mathrm{Q}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\left(\:\mathrm{26}\:!\:\right)^{\:\mathrm{58}} \:+\:\mathrm{k}\:\overset{\:\mathrm{29}} {\equiv}\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{and}\:,\:\:\mathrm{k}\:\in\:\mathbb{N}\:,\:\:\mathrm{find}:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{Min}\:\left(\:\mathrm{k}\:\right)=? \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 11/Jul/22
![(29−1)!≡−1(mod 29) [Wilson′s theorem] 28!≡−1+29(mod 29) 28!≡28(mod 29) 27!≡1(mod 29) 27!≡1+29×13(mod 29) 27!≡378(mod 29) 26!≡14(mod 29) (26!)^2 ≡14^2 ≡22(mod 29).....(i) (26!)^(28) ≡14^(28) ≡1(mod 29) {(26!)^(28) }^2 ≡1^2 (mod 29)........(ii) (i)×(ii) (26!)^(56) ∙(26!)^2 ≡1∙22(mod 29) (26!)^(58) ≡22−29=−7(mod 29) (26!)^(58) +7≡0(mod 29) (26!)^(58) +7+29m≡0(mod 29) k=7+29m [k∈N⇒m≥0] m=0: min(k)=7](https://www.tinkutara.com/question/Q173413.png)
$$\left(\mathrm{29}−\mathrm{1}\right)!\equiv−\mathrm{1}\left({mod}\:\mathrm{29}\right)\:\left[{Wilson}'{s}\:{theorem}\right] \\ $$$$\mathrm{28}!\equiv−\mathrm{1}+\mathrm{29}\left({mod}\:\mathrm{29}\right) \\ $$$$\mathrm{28}!\equiv\mathrm{28}\left({mod}\:\mathrm{29}\right) \\ $$$$\mathrm{27}!\equiv\mathrm{1}\left({mod}\:\mathrm{29}\right) \\ $$$$\mathrm{27}!\equiv\mathrm{1}+\mathrm{29}×\mathrm{13}\left({mod}\:\mathrm{29}\right) \\ $$$$\mathrm{27}!\equiv\mathrm{378}\left({mod}\:\mathrm{29}\right) \\ $$$$\mathrm{26}!\equiv\mathrm{14}\left({mod}\:\mathrm{29}\right) \\ $$$$\left(\mathrm{26}!\right)^{\mathrm{2}} \equiv\mathrm{14}^{\mathrm{2}} \equiv\mathrm{22}\left({mod}\:\mathrm{29}\right)…..\left({i}\right) \\ $$$$\left(\mathrm{26}!\right)^{\mathrm{28}} \equiv\mathrm{14}^{\mathrm{28}} \equiv\mathrm{1}\left({mod}\:\mathrm{29}\right) \\ $$$$\left\{\left(\mathrm{26}!\right)^{\mathrm{28}} \right\}^{\mathrm{2}} \equiv\mathrm{1}^{\mathrm{2}} \left({mod}\:\mathrm{29}\right)……..\left({ii}\right) \\ $$$$\left({i}\right)×\left({ii}\right) \\ $$$$\left(\mathrm{26}!\right)^{\mathrm{56}} \centerdot\left(\mathrm{26}!\right)^{\mathrm{2}} \equiv\mathrm{1}\centerdot\mathrm{22}\left({mod}\:\mathrm{29}\right) \\ $$$$\left(\mathrm{26}!\right)^{\mathrm{58}} \equiv\mathrm{22}−\mathrm{29}=−\mathrm{7}\left({mod}\:\mathrm{29}\right) \\ $$$$\left(\mathrm{26}!\right)^{\mathrm{58}} +\mathrm{7}\equiv\mathrm{0}\left({mod}\:\mathrm{29}\right) \\ $$$$\left(\mathrm{26}!\right)^{\mathrm{58}} +\mathrm{7}+\mathrm{29}{m}\equiv\mathrm{0}\left({mod}\:\mathrm{29}\right) \\ $$$${k}=\mathrm{7}+\mathrm{29}{m}\:\left[{k}\in\mathbb{N}\Rightarrow{m}\geqslant\mathrm{0}\right] \\ $$$${m}=\mathrm{0}:\:{min}\left({k}\right)=\mathrm{7}\: \\ $$
Commented by mnjuly1970 last updated on 11/Jul/22

$$\mathrm{thanks}\:\mathrm{alot}\:\mathrm{sir}\: \\ $$
