Menu Close

Q-a-n-is-an-arithmatic-sequence-a-first-term-and-d-difference-such-that-a-a-a-d-a-ad-find-a-n-no

Tinku Tara 0 Comments
Pin




Question Number 173926 by mnjuly1970 last updated on 21/Jul/22
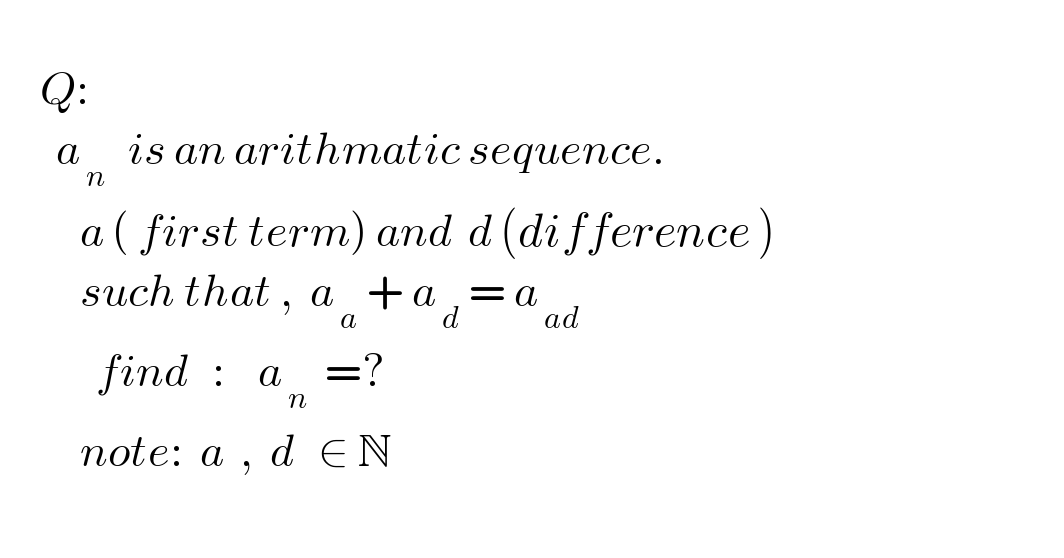
Q: a_( n ) is an arithmatic sequence. a ( first term) and d (difference ) such that , a_( a) + a_( d) = a_( ad) find : a_( n) =? note: a , d ∈ N
$$ \\ $$$$\:\:\:\:\:{Q}: \\ $$$$\:\:\:\:\:\:\:{a}_{\:{n}\:} \:\:{is}\:{an}\:{arithmatic}\:{sequence}. \\ $$$$\:\:\:\:\:\:\:\:\:\:{a}\:\left(\:{first}\:{term}\right)\:{and}\:\:{d}\:\left({difference}\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:{such}\:{that}\:,\:\:{a}_{\:{a}} \:+\:{a}_{\:{d}} \:=\:{a}_{\:{ad}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{find}\:\:\::\:\:\:\:{a}_{\:{n}} \:\:=? \\ $$$$\:\:\:\:\:\:\:\:\:\:{note}:\:\:{a}\:\:,\:\:{d}\:\:\:\in\:\mathbb{N}\:\: \\ $$$$\:\:\:\:\:\:\: \\ $$
Commented by Rasheed.Sindhi last updated on 21/Jul/22
a ( first term) and d (differece)
$$\:{a}\:\left(\:{first}\:{term}\right)\:{and}\:\:{d}\:\left({differece}\right) \\ $$
Commented by mnjuly1970 last updated on 21/Jul/22
grateful sir Rashid
$$\:\:{grateful}\:{sir}\:{Rashid} \\ $$
Commented by Rasheed.Sindhi last updated on 21/Jul/22
ThanX mnjuly sir!
$$\:\:\mathbb{T}\boldsymbol{\mathrm{han}}\mathbb{X}\:{mnjuly}\:{sir}! \\ $$
Answered by mahdipoor last updated on 21/Jul/22
⇒[a+(a−1)d]+[a+(d−1)d]=[a+(ad−1)d] ⇒a+ad+d^2 −d=ad^2 ⇒a(1+d−d^2 )=d−d^2 ⇒a=((d−d^2 )/(d−d^2 −1))∈N⇒ { ((d−d^2 =ma)),((d−d^2 −1=m∈Z)) :}⇒1=m(a−1)⇒ { ((m=−1,a=0 ⇒d−d^2 =0⇒d=0,1)),((m=1,a=2 ⇒d−d^2 =2⇒∄d∈N)) :} ⇒⇒ { ((ans 1: a_n =0 with a=0 , d=0 )),((ans 2: a_n =n−1 with a=0 , d=1)) :}
$$\Rightarrow\left[{a}+\left({a}−\mathrm{1}\right){d}\right]+\left[{a}+\left({d}−\mathrm{1}\right){d}\right]=\left[{a}+\left({ad}−\mathrm{1}\right){d}\right] \\ $$$$\Rightarrow{a}+{ad}+{d}^{\mathrm{2}} −{d}={ad}^{\mathrm{2}} \\ $$$$\Rightarrow{a}\left(\mathrm{1}+{d}−{d}^{\mathrm{2}} \right)={d}−{d}^{\mathrm{2}} \Rightarrow{a}=\frac{{d}−{d}^{\mathrm{2}} }{{d}−{d}^{\mathrm{2}} −\mathrm{1}}\in\mathrm{N}\Rightarrow \\ $$$$\begin{cases}{{d}−{d}^{\mathrm{2}} ={ma}}\\{{d}−{d}^{\mathrm{2}} −\mathrm{1}={m}\in\mathrm{Z}}\end{cases}\Rightarrow\mathrm{1}={m}\left({a}−\mathrm{1}\right)\Rightarrow \\ $$$$\begin{cases}{{m}=−\mathrm{1},{a}=\mathrm{0}\:\Rightarrow{d}−{d}^{\mathrm{2}} \:=\mathrm{0}\Rightarrow{d}=\mathrm{0},\mathrm{1}}\\{{m}=\mathrm{1},{a}=\mathrm{2}\:\Rightarrow{d}−{d}^{\mathrm{2}} =\mathrm{2}\Rightarrow\nexists{d}\in\mathrm{N}}\end{cases} \\ $$$$\Rightarrow\Rightarrow\:\begin{cases}{{ans}\:\mathrm{1}:\:{a}_{{n}} =\mathrm{0}\:\:\:\:\:\:\:\:\:{with}\:\:{a}=\mathrm{0}\:,\:{d}=\mathrm{0}\:\:\:\:\:\:\:\:\:\:}\\{{ans}\:\mathrm{2}:\:{a}_{{n}} ={n}−\mathrm{1}\:\:{with}\:\:{a}=\mathrm{0}\:,\:{d}=\mathrm{1}}\end{cases} \\ $$
Commented by Tawa11 last updated on 21/Jul/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by Rasheed.Sindhi last updated on 21/Jul/22
a_n =a+(n−1)d a_a =a+(a−1)d , a_d =a+(d−1)d, a_(ad) =a+(ad−1)d a_a +a_d =a_(ad) ⇒a+(a−1)d+a+(d−1)d =a+(ad−1)d ⇒2a+(a+d−2)d=a+(ad−1)d a+(a+d−2−ad+1)d=0 a+(a+d−ad−1)d=0 a+ad+d^2 −ad^2 −d=0 a(1+d−d^2 )=−d^2 +d a=((d^2 −d)/(d^2 −d−1))∈N⇒d^2 −d−1 ∣ d^2 −d d^2 −d=0 ∨ d^2 −d−1=1 d(d−1)=0 ∨ d(d−1)=2 d=0^(×) ,1,2⇒a=0^(×) ,0^(×) ,2 ⇒d=2⇒a=2 ✓ a_n =2+(n−1)(2)=2+2n−2=2n determinant (((a_n =2n))) 2,4,6,8,... Verification: a_a =a+(a−1)d or a_d =a+(d−1)d a_2 =2+(2−1)(2)=4 a_(ad) =a+(ad−1)d a_(2×2) =2+3×2=8 a_4 =8 a_a +a_d =a_(ad) a_2 +a_2 =a_4 4+4=8
$${a}_{{n}} ={a}+\left({n}−\mathrm{1}\right){d} \\ $$$${a}_{{a}} ={a}+\left({a}−\mathrm{1}\right){d}\:\:,\:\:{a}_{{d}} ={a}+\left({d}−\mathrm{1}\right){d}, \\ $$$${a}_{{ad}} ={a}+\left({ad}−\mathrm{1}\right){d} \\ $$$$ \\ $$$${a}_{{a}} +{a}_{{d}} ={a}_{{ad}} \\ $$$$\Rightarrow{a}+\left({a}−\mathrm{1}\right){d}+{a}+\left({d}−\mathrm{1}\right){d} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={a}+\left({ad}−\mathrm{1}\right){d} \\ $$$$\Rightarrow\mathrm{2}{a}+\left({a}+{d}−\mathrm{2}\right){d}={a}+\left({ad}−\mathrm{1}\right){d} \\ $$$$\:\:\:\:\:\:{a}+\left({a}+{d}−\mathrm{2}−{ad}+\mathrm{1}\right){d}=\mathrm{0} \\ $$$$\:\:\:\:\:\:{a}+\left({a}+{d}−{ad}−\mathrm{1}\right){d}=\mathrm{0} \\ $$$$\:\:\:\:\:{a}+{ad}+{d}^{\mathrm{2}} −{ad}^{\mathrm{2}} −{d}=\mathrm{0} \\ $$$${a}\left(\mathrm{1}+{d}−{d}^{\mathrm{2}} \right)=−{d}^{\mathrm{2}} +{d} \\ $$$${a}=\frac{{d}^{\mathrm{2}} −{d}}{{d}^{\mathrm{2}} −{d}−\mathrm{1}}\in\mathbb{N}\Rightarrow{d}^{\mathrm{2}} −{d}−\mathrm{1}\:\mid\:{d}^{\mathrm{2}} −{d} \\ $$$${d}^{\mathrm{2}} −{d}=\mathrm{0}\:\vee\:{d}^{\mathrm{2}} −{d}−\mathrm{1}=\mathrm{1} \\ $$$${d}\left({d}−\mathrm{1}\right)=\mathrm{0}\:\vee\:{d}\left({d}−\mathrm{1}\right)=\mathrm{2} \\ $$$${d}=\overset{×} {\mathrm{0}},\mathrm{1},\mathrm{2}\Rightarrow{a}=\overset{×} {\mathrm{0}},\overset{×} {\mathrm{0}},\mathrm{2} \\ $$$$\Rightarrow{d}=\mathrm{2}\Rightarrow{a}=\mathrm{2}\:\checkmark \\ $$$${a}_{{n}} =\mathrm{2}+\left({n}−\mathrm{1}\right)\left(\mathrm{2}\right)=\mathrm{2}+\mathrm{2}{n}−\mathrm{2}=\mathrm{2}{n} \\ $$$$\begin{array}{|c|}{{a}_{{n}} =\mathrm{2}{n}}\\\hline\end{array} \\ $$$$\mathrm{2},\mathrm{4},\mathrm{6},\mathrm{8},…\:\:\: \\ $$$${Verification}: \\ $$$${a}_{{a}} ={a}+\left({a}−\mathrm{1}\right){d}\:{or}\:{a}_{{d}} ={a}+\left({d}−\mathrm{1}\right){d} \\ $$$${a}_{\mathrm{2}} =\mathrm{2}+\left(\mathrm{2}−\mathrm{1}\right)\left(\mathrm{2}\right)=\mathrm{4} \\ $$$${a}_{{ad}} ={a}+\left({ad}−\mathrm{1}\right){d} \\ $$$${a}_{\mathrm{2}×\mathrm{2}} =\mathrm{2}+\mathrm{3}×\mathrm{2}=\mathrm{8} \\ $$$${a}_{\mathrm{4}} =\mathrm{8} \\ $$$${a}_{{a}} +{a}_{{d}} ={a}_{{ad}} \\ $$$${a}_{\mathrm{2}} +{a}_{\mathrm{2}} ={a}_{\mathrm{4}} \\ $$$$\mathrm{4}+\mathrm{4}=\mathrm{8} \\ $$
Commented by mnjuly1970 last updated on 21/Jul/22
thanks alot sir
$${thanks}\:{alot}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *