Question Number 40466 by naziri2013@ last updated on 22/Jul/18
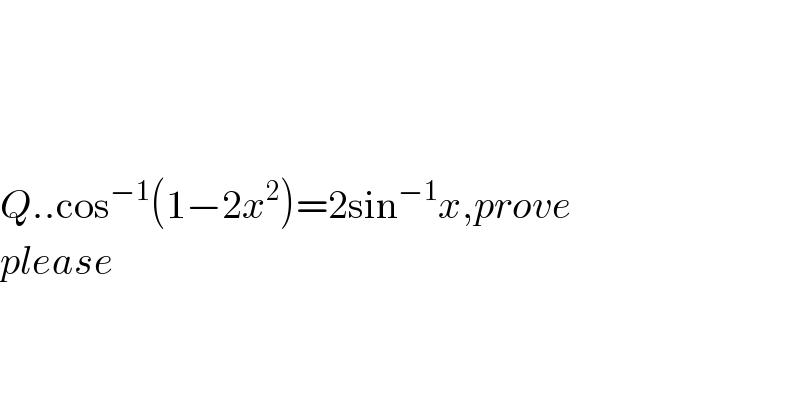
$$ \\ $$$$ \\ $$$$ \\ $$$${Q}..\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \right)=\mathrm{2sin}^{−\mathrm{1}} {x},{prove}\:\:\: \\ $$$${please} \\ $$$$ \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 22/Jul/18
![let prove that arccos(1−2x^2 )=2arcsinx let f(x)=arccos(1−2x^2 )−2arcsinx D_f ? x∈ D_f ⇔ −1≤x≤1 and −1≤1−2x^2 ≤1 but −1≤1−2x^2 ≤1 ⇔−2≤−2x^2 ≤0 ⇔ 0≤2x^2 ≤2 ⇔0≤x^2 ≤1 ⇔ −1≤x≤1 ⇒ D_f =[−1,1] we have f^′ (x)= ((−(−4x))/( (√(1−(1−2x^2 )^2 )))) − (2/( (√(1−x^2 )))) =((4x(√(1−x^2 )) −2(√(1−(4x^4 −4x^2 +1))))/( (√(1−x^2 ))(√(1−(1−2x^2 )^2 )))) =((4x(√(1−x^2 )) −2(√(4x^2 −4x^4 )))/( (√(1−x^2 ))(√(4x^2 −4x^4 )))) = ((4x(√(1−x^2 )) −4∣x∣(√(1−x^2 )))/( (√(1−x^2 ))(√(4x^2 −4x^4 )))) if 0<x<1 we have f^′ (x)=0 ⇒f(x)=c ∀ x∈[0,1] f(x)=f(0)=0 if x∈]−1,0[ f^′ (x)= ((8x(√(1−x^2 )))/(−2x(1−x^2 ))) =((−4)/( (√(1−x^2 )))) ≠0 ⇒f is not constant finally we have arccos(1−2x^2 )=2 arcsinx if x∈[0,1] .](https://www.tinkutara.com/question/Q40468.png)
$${let}\:{prove}\:{that}\:\:{arccos}\left(\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \right)=\mathrm{2}{arcsinx}\:\:\:{let} \\ $$$${f}\left({x}\right)={arccos}\left(\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \right)−\mathrm{2}{arcsinx}\:\:\:\:{D}_{{f}} \:\:? \\ $$$${x}\in\:{D}_{{f}} \:\:\Leftrightarrow\:−\mathrm{1}\leqslant{x}\leqslant\mathrm{1}\:{and}\:−\mathrm{1}\leqslant\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \leqslant\mathrm{1}\:{but} \\ $$$$−\mathrm{1}\leqslant\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \leqslant\mathrm{1}\:\Leftrightarrow−\mathrm{2}\leqslant−\mathrm{2}{x}^{\mathrm{2}} \leqslant\mathrm{0}\:\:\Leftrightarrow\:\mathrm{0}\leqslant\mathrm{2}{x}^{\mathrm{2}} \leqslant\mathrm{2}\:\Leftrightarrow\mathrm{0}\leqslant{x}^{\mathrm{2}} \leqslant\mathrm{1}\:\Leftrightarrow\:−\mathrm{1}\leqslant{x}\leqslant\mathrm{1}\:\Rightarrow \\ $$$${D}_{{f}} =\left[−\mathrm{1},\mathrm{1}\right]\:{we}\:{have} \\ $$$${f}^{'} \left({x}\right)=\:\frac{−\left(−\mathrm{4}{x}\right)}{\:\sqrt{\mathrm{1}−\left(\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \right)^{\mathrm{2}} }}\:−\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:=\frac{\mathrm{4}{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:−\mathrm{2}\sqrt{\mathrm{1}−\left(\mathrm{4}{x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{2}} \:+\mathrm{1}\right)}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\sqrt{\mathrm{1}−\left(\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \right)^{\mathrm{2}} }} \\ $$$$=\frac{\mathrm{4}{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:−\mathrm{2}\sqrt{\mathrm{4}{x}^{\mathrm{2}} \:−\mathrm{4}{x}^{\mathrm{4}} }}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{4}} }}\:=\:\frac{\mathrm{4}{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:−\mathrm{4}\mid{x}\mid\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{4}} }} \\ $$$${if}\:\:\mathrm{0}<{x}<\mathrm{1}\:\:{we}\:{have}\:{f}^{'} \left({x}\right)=\mathrm{0}\:\Rightarrow{f}\left({x}\right)={c}\:\:\forall\:{x}\in\left[\mathrm{0},\mathrm{1}\right]\: \\ $$$${f}\left({x}\right)={f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\left.{if}\:{x}\in\right]−\mathrm{1},\mathrm{0}\left[\:\:{f}^{'} \left({x}\right)=\:\frac{\mathrm{8}{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{−\mathrm{2}{x}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}\:=\frac{−\mathrm{4}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\neq\mathrm{0}\:\Rightarrow{f}\:{is}\:{not}\:{constant}\right. \\ $$$${finally}\:\:{we}\:{have}\:{arccos}\left(\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \right)=\mathrm{2}\:{arcsinx}\:{if}\:{x}\in\left[\mathrm{0},\mathrm{1}\right]\:. \\ $$
Commented by prakash jain last updated on 22/Jul/18
![This is not true in general range of cos^(−1) is [0,π] range of sin^(−1) is [−(π/2),(π/2)] put x=−(1/2) 2sin^(−1) x=−(π/3) cos^(−1) (1−2x^2 )=cos^(−1) (1/2)=(π/3)](https://www.tinkutara.com/question/Q40491.png)
$$\mathrm{This}\:\mathrm{is}\:\mathrm{not}\:\mathrm{true}\:\mathrm{in}\:\mathrm{general} \\ $$$$\mathrm{range}\:\mathrm{of}\:\mathrm{cos}\:^{−\mathrm{1}} \:\mathrm{is}\:\left[\mathrm{0},\pi\right] \\ $$$$\mathrm{range}\:\mathrm{of}\:\mathrm{sin}\:^{−\mathrm{1}} \:\mathrm{is}\:\left[−\frac{\pi}{\mathrm{2}},\frac{\pi}{\mathrm{2}}\right] \\ $$$$\mathrm{put}\:{x}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{2sin}^{−\mathrm{1}} {x}=−\frac{\pi}{\mathrm{3}} \\ $$$$\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \right)=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}=\frac{\pi}{\mathrm{3}} \\ $$
Commented by prakash jain last updated on 22/Jul/18

$$\mathrm{also}\:\mathrm{note}\:\mathrm{that} \\ $$$$\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin}\:{x}\right)\:\mathrm{does}\:\mathrm{not}\:\mathrm{always}\:\mathrm{equal} \\ $$$${x}\:\mathrm{due}\:\mathrm{to}\:\mathrm{restriction}\:\mathrm{on}\:\mathrm{range}\:\mathrm{of} \\ $$$$\mathrm{sin}^{−\mathrm{1}} {x}. \\ $$$$\mathrm{sin}\:\left(\mathrm{sin}^{−\mathrm{1}} {x}\right)\:\mathrm{however}\:\mathrm{always}\:\mathrm{equals}\:{x}. \\ $$
Commented by prof Abdo imad last updated on 23/Jul/18
![i have proved that equality is true in[0,1] and x=−(1/2) ∉[0,1] !](https://www.tinkutara.com/question/Q40503.png)
$${i}\:{have}\:{proved}\:{that}\:{equality}\:{is}\:{true}\:{in}\left[\mathrm{0},\mathrm{1}\right]\:{and} \\ $$$${x}=−\frac{\mathrm{1}}{\mathrm{2}}\:\notin\left[\mathrm{0},\mathrm{1}\right]\:! \\ $$
Commented by prakash jain last updated on 23/Jul/18

$$\mathrm{M}{y}\:\mathrm{comment}\:\mathrm{was}\:\mathrm{for}\:\mathrm{the}\:\mathrm{question}.\:\mathrm{The} \\ $$$$\mathrm{questioner}\:\mathrm{seems}\:\mathrm{to}\:\mathrm{be}\:\mathrm{a}\:\mathrm{student}\:\mathrm{so} \\ $$$$\mathrm{wanted}\:\mathrm{to}\:\mathrm{highlight}\:\mathrm{common} \\ $$$$\mathrm{mistakes}\:\mathrm{made}\:\mathrm{while}\:\mathrm{using} \\ $$$$\mathrm{inverse}\:\mathrm{trignimetric}\:\mathrm{functions}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Jul/18

$${x}={sin}\theta \\ $$$${cos}^{−\mathrm{1}} \left(\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} \theta\right) \\ $$$${cos}^{−\mathrm{1}} \left({cos}\mathrm{2}\theta\right)=\mathrm{2}\theta \\ $$$$\: \\ $$$$\mathrm{2}{sin}^{−\mathrm{1}} \left({sin}\theta\right) \\ $$$$\mathrm{2}\theta \\ $$$$ \\ $$
