Question Number 48239 by olj55336@awsoo.com last updated on 21/Nov/18
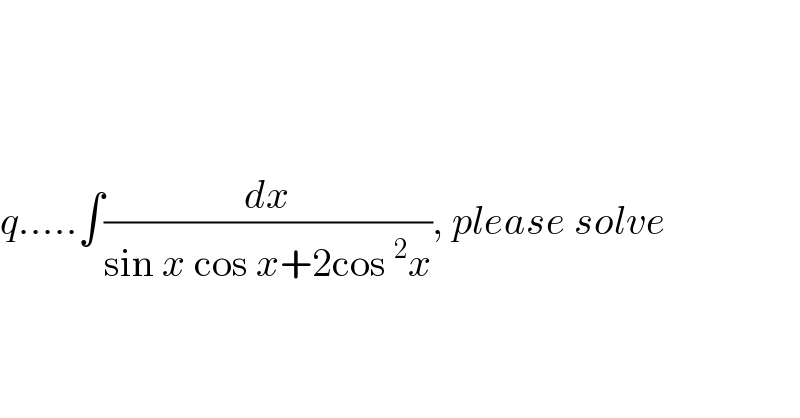
$$ \\ $$$$ \\ $$$$ \\ $$$${q}…..\int\frac{{dx}}{\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}+\mathrm{2cos}\:^{\mathrm{2}} {x}},\:{please}\:{solve} \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 21/Nov/18
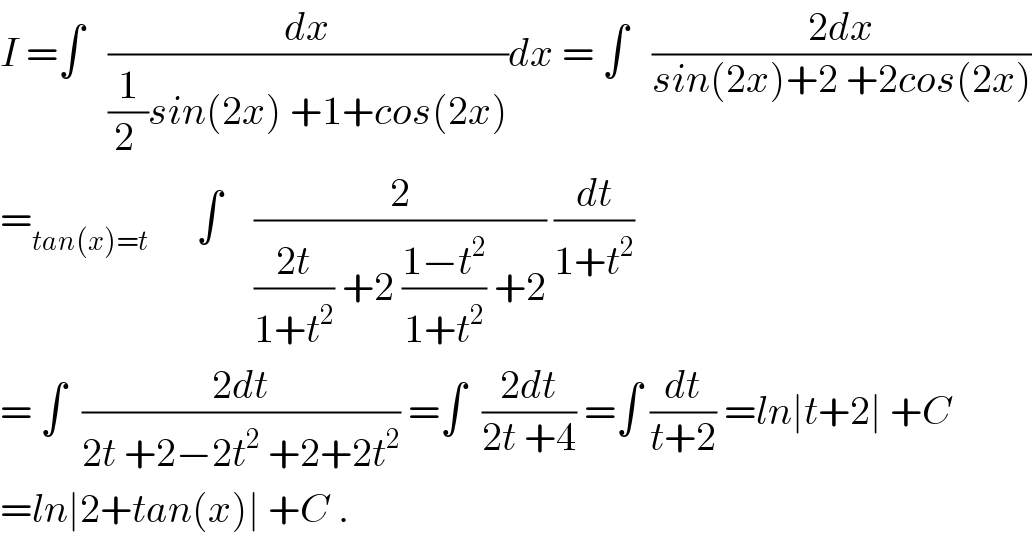
$${I}\:=\int\:\:\:\frac{{dx}}{\frac{\mathrm{1}}{\mathrm{2}\:}{sin}\left(\mathrm{2}{x}\right)\:+\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)}{dx}\:=\:\int\:\:\:\frac{\mathrm{2}{dx}}{{sin}\left(\mathrm{2}{x}\right)+\mathrm{2}\:+\mathrm{2}{cos}\left(\mathrm{2}{x}\right)} \\ $$$$=_{{tan}\left({x}\right)={t}} \:\:\:\:\:\:\int\:\:\:\:\frac{\mathrm{2}}{\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\:+\mathrm{2}\:\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:+\mathrm{2}}\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\:\int\:\:\frac{\mathrm{2}{dt}}{\mathrm{2}{t}\:+\mathrm{2}−\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{2}+\mathrm{2}{t}^{\mathrm{2}} }\:=\int\:\:\frac{\mathrm{2}{dt}}{\mathrm{2}{t}\:+\mathrm{4}}\:=\int\:\frac{{dt}}{{t}+\mathrm{2}}\:={ln}\mid{t}+\mathrm{2}\mid\:+{C} \\ $$$$={ln}\mid\mathrm{2}+{tan}\left({x}\right)\mid\:+{C}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Nov/18
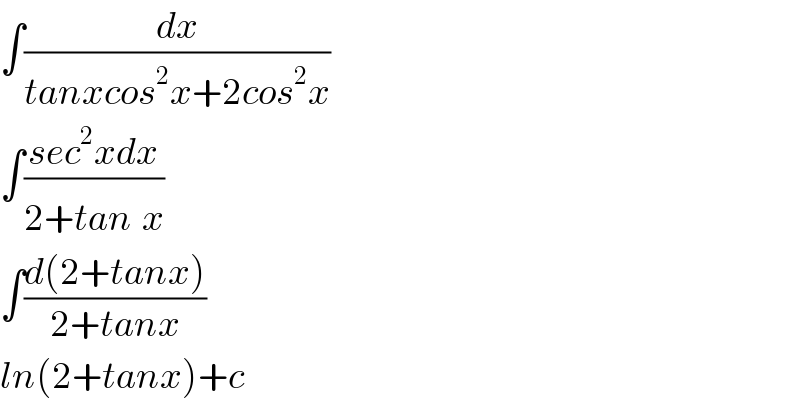
$$\int\frac{{dx}}{{tanxcos}^{\mathrm{2}} {x}+\mathrm{2}{cos}^{\mathrm{2}} {x}} \\ $$$$\int\frac{{sec}^{\mathrm{2}} {xdx}}{\mathrm{2}+{tan}^{} {x}} \\ $$$$\int\frac{{d}\left(\mathrm{2}+{tanx}\right)}{\mathrm{2}+{tanx}} \\ $$$${ln}\left(\mathrm{2}+{tanx}\right)+{c} \\ $$
