Question Number 185890 by mnjuly1970 last updated on 29/Jan/23
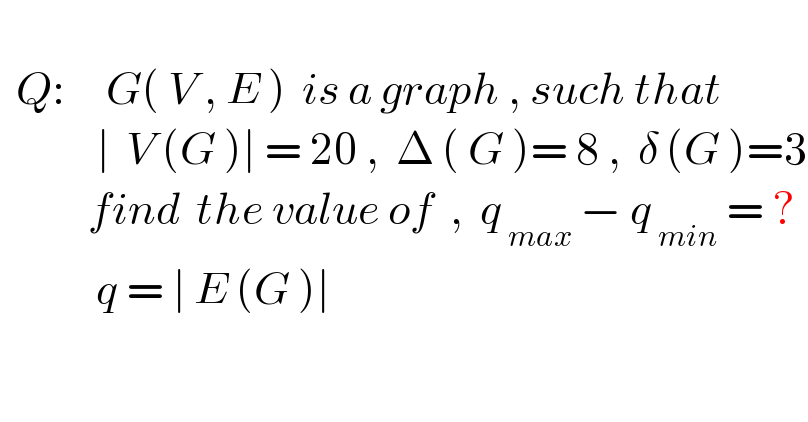
$$ \\ $$$$\:\:{Q}:\:\:\:\:\:{G}\left(\:{V}\:,\:{E}\:\right)\:\:{is}\:{a}\:{graph}\:,\:{such}\:{that} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mid\:\:{V}\:\left({G}\:\right)\mid\:=\:\mathrm{20}\:,\:\:\Delta\:\left(\:{G}\:\right)=\:\mathrm{8}\:,\:\:\delta\:\left({G}\:\right)=\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{find}\:\:{the}\:{value}\:{of}\:\:,\:\:{q}_{\:{max}} \:−\:{q}_{\:{min}} \:=\:? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{q}\:=\:\mid\:{E}\:\left({G}\:\right)\mid\:\: \\ $$
Answered by MrGaster last updated on 02/Nov/24

$${q}_{{mam}} −{q}_{{mim}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\underset{{v}\in{V}\left({G}\right)} {\sum}\Delta\left({G}\right)−\underset{{v}\in{V}\left({G}\right)} {\sum}\delta\left({G}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{20}\centerdot\mathrm{8}−\mathrm{20}\centerdot\mathrm{3}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{160}−\mathrm{60}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\centerdot\mathrm{100} \\ $$$$=\mathrm{50} \\ $$
