Question Number 147285 by mnjuly1970 last updated on 19/Jul/21
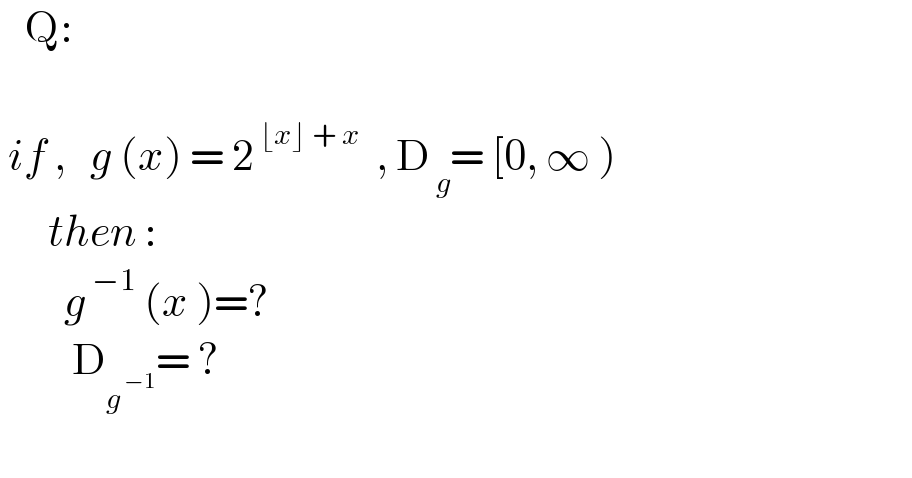
$$\:\:\:\mathrm{Q}: \\ $$$$ \\ $$$$\:{if}\:,\:\:\:{g}\:\left({x}\right)\:=\:\mathrm{2}^{\:\lfloor{x}\rfloor\:+\:{x}} \:\:,\:\mathrm{D}_{\:{g}} =\:\left[\mathrm{0},\:\infty\:\right) \\ $$$$\:\:\:\:\:\:{then}\:: \\ $$$$\:\:\:\:\:\:\:\:{g}^{\:−\mathrm{1}} \:\left({x}\:\right)=? \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{D}_{{g}^{\:−\mathrm{1}} } =\:? \\ $$$$ \\ $$
Answered by Olaf_Thorendsen last updated on 19/Jul/21

$$\mathrm{D}_{{g}} \:=\:\left[\mathrm{0}\:;\:+\infty\left[\:=\:\underset{{k}\in\mathbb{N}} {\cup}\left[{k}\:;\:{k}+\mathrm{1}\left[\right.\right.\right.\right. \\ $$$$\mathrm{Let}\:\mathrm{D}_{{k}} \:=\:\left[{k}\:;\:{k}+\mathrm{1}\left[,\:\mathrm{D}\:=\:\underset{{k}\in\mathbb{N}} {\cup}\mathrm{D}_{{k}} \right.\right. \\ $$$$\forall{x}\in\mathrm{D}_{{k}} ,\:{g}\left({x}\right)\:=\:\mathrm{2}^{\lfloor{x}\rfloor+{x}} \:=\:\mathrm{2}^{{x}+{k}} \\ $$$${x}+{k}\:=\:\frac{\mathrm{ln}\left({g}\left({x}\right)\right)}{\mathrm{ln2}}\:=\:\mathrm{log}_{\mathrm{2}} \left({g}\left({x}\right)\right) \\ $$$${x}\:=\:\mathrm{log}_{\mathrm{2}} \left({g}\left({x}\right)\right)−{k} \\ $$$$\Rightarrow\:{g}^{−\mathrm{1}} \left({x}\right)\:=\:\mathrm{log}_{\mathrm{2}} \left({x}\right)−{k} \\ $$$$\:{g}^{−\mathrm{1}} \left(\mathrm{D}_{{k}} \right)\:=\:{g}^{−\mathrm{1}} \left(\left[{k}\:;\:{k}+\mathrm{1}\left[\right)\right.\right. \\ $$$$\:{g}^{−\mathrm{1}} \left(\mathrm{D}_{{k}} \right)\:=\:\left[\mathrm{log}_{\mathrm{2}} \left({k}\right)−{k}\:;\:\mathrm{log}_{\mathrm{2}} \left({k}+\mathrm{1}\right)−{k}\left[\right.\right. \\ $$$$\:\mathrm{D}_{{k}} ^{−\mathrm{1}} \:=\:\left[\mathrm{log}_{\mathrm{2}} \left({k}\right)−{k}\:;\:\mathrm{log}_{\mathrm{2}} \left({k}+\mathrm{1}\right)−{k}\left[\right.\right. \\ $$$$\mathrm{D}_{{g}^{−\mathrm{1}} } \:=\:\underset{{k}\in\mathbb{N}} {\cup}\mathrm{D}_{{k}} ^{−\mathrm{1}} \\ $$
