Q-in-AB-C-A-90-o-and-m-b-2-m-c-2-100-find-the-value-of-a-note-m-a-the-median-corresponding-

Question Number 176100 by mnjuly1970 last updated on 12/Sep/22

Q :

i n A \overset{Δ}{B C} : A = 90^{o} a n d, m_{b}^{2} + m_{c}^{2} = 100 .

f i n d t h e v a l u e o f^{″} a^{″} .

n o t e : ⟨ m_{a} := t h e m e d i a n c o r r e s p o n d i n g t o^{″} A^{″} .

- - - m . n - - -

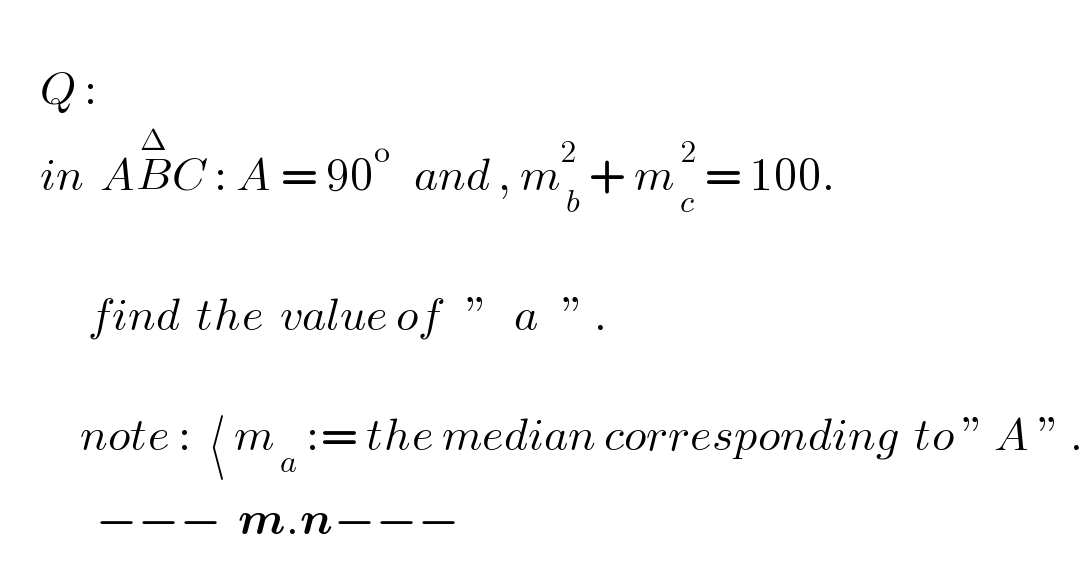
Answered by Rasheed.Sindhi last updated on 12/Sep/22

∙ a^{2} = b^{2} + c^{2}

∙ b^{2} + {(\frac{c}{2})}^{2} = m_{c}^{2}

∙ c^{2} + {(\frac{b}{2})}^{2} = m_{b}^{2}

m_{b}^{2} + m_{c}^{2}

= {c^{2} + {(\frac{b}{2})}^{2}} + {b^{2} + {(\frac{c}{2})}^{2}} = 100

c^{2} + \frac{b^{2}}{4} + b^{2} + \frac{c^{2}}{4} = 100

5 b^{2} + 5 c^{2} = 400

b^{2} + c^{2} = 80

a^{2} = 80

a = \sqrt{80} = 4 \sqrt{5}

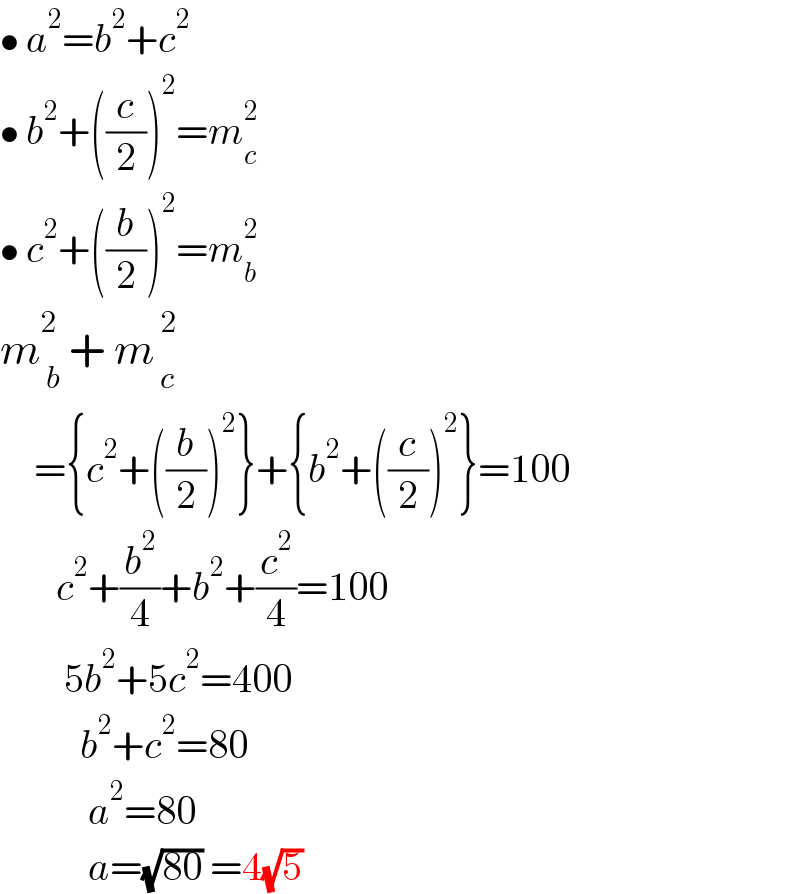
Commented by mnjuly1970 last updated on 12/Sep/22

g r a t e f u l s i r r a s h e e d

Answered by behi834171 last updated on 13/Sep/22

2 m_{b} = a^{2} + c^{2} - \frac{b^{2}}{2}

2 m_{c} = a^{2} + b^{2} - \frac{c^{2}}{2} \Rightarrow 2 (m_{b}^{2} + m_{c}^{2}) = 2 a^{2} + \frac{a^{2}}{2} \Rightarrow

m_{b}^{2} + m_{c}^{2} = \frac{5 a^{2}}{4} = 5 {(\frac{a}{2})}^{2} = 5 m_{a}^{2}

\Rightarrow 200 = \frac{5 a^{2}}{2} \Rightarrow a = \sqrt{80} = 4 \sqrt{5} .

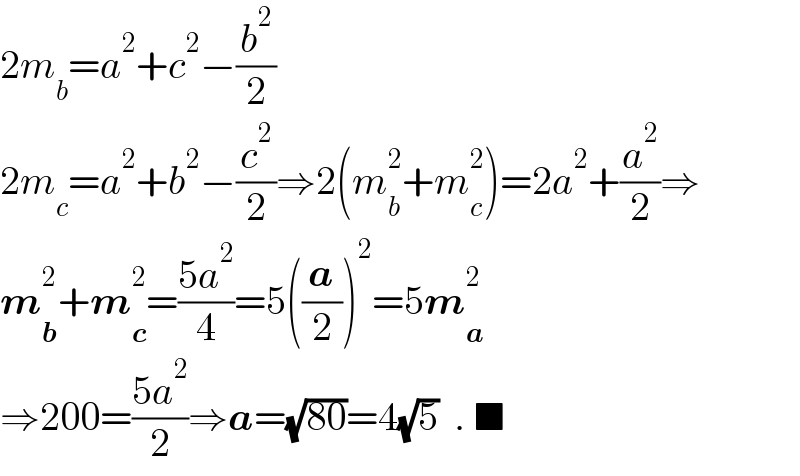
Commented by mnjuly1970 last updated on 13/Sep/22

m a m n o o n o s t a d

Commented by behi834171 last updated on 13/Sep/22

[n o t e :

w h e n : ∡ A = 90^{∙} \Rightarrow m_{a} = \frac{a}{2}, m_{b}^{2} + m_{c}^{2} = 5 m_{a}^{2}

\Rightarrow m_{a}^{2} = \frac{m_{b}^{2} + m_{c}^{2}}{5} = \frac{100}{5} = 20

\Rightarrow m_{a} = 2 \sqrt{5} \Rightarrow a = 2 m_{a} = 4 \sqrt{5} .]