Menu Close

Q-N-Find-the-coefficint-of-x-4-in-the-expansion-of-1-3x-10x-2-x-1-x-10-

Tinku Tara 0 Comments
Pin




Question Number 27946 by das47955@mail.com last updated on 17/Jan/18
Q.N− Find the coefficint of x^4 in the expansion of (1+3x+10x^2 )(x+(1/x))^(10)
$$\boldsymbol{\mathrm{Q}}.\boldsymbol{\mathrm{N}}− \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\mathrm{Find}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{coefficint}}\:\boldsymbol{\mathrm{of}}\:\:\boldsymbol{\mathrm{x}}^{\mathrm{4}} \\ $$$$\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{expansion}}\:\boldsymbol{\mathrm{of}} \\ $$$$\:\:\:\:\:\left(\mathrm{1}+\mathrm{3}\boldsymbol{\mathrm{x}}+\mathrm{10}\boldsymbol{\mathrm{x}}^{\mathrm{2}} \right)\left(\boldsymbol{\mathrm{x}}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}\right)^{\mathrm{10}} \\ $$$$ \\ $$$$\:\:\:\:\:\:\: \\ $$
Answered by Rasheed.Sindhi last updated on 17/Jan/18
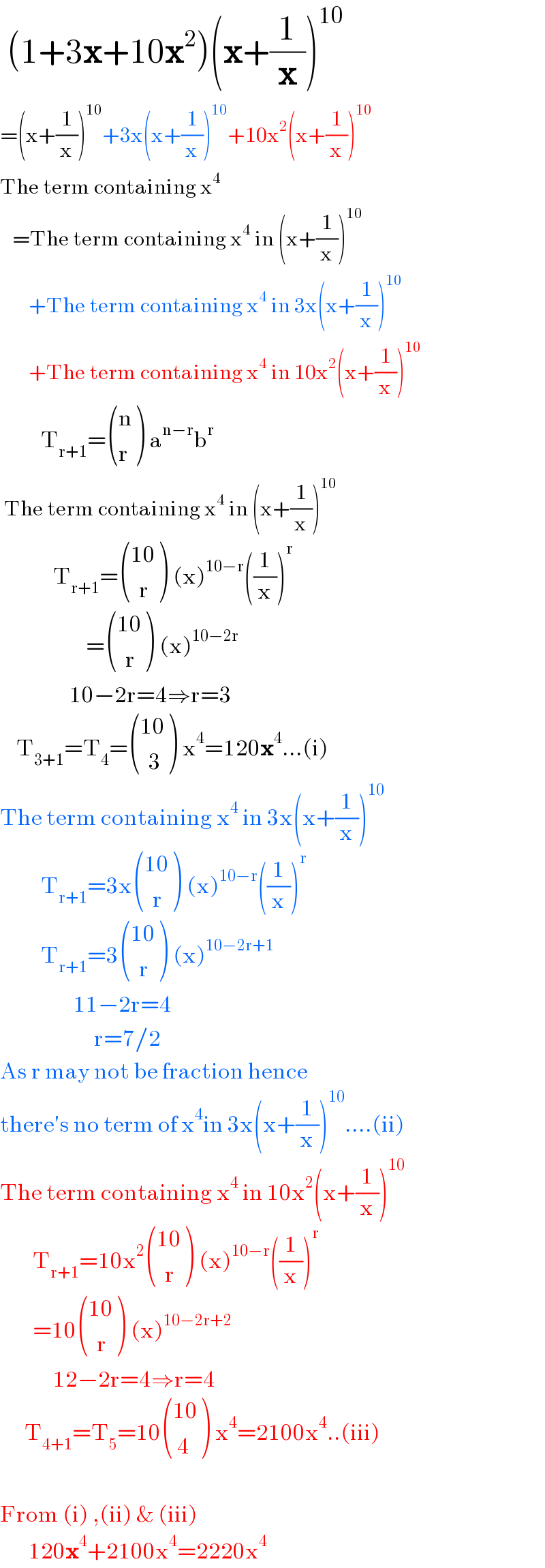
(1+3x+10x^2 )(x+(1/x))^(10) =(x+(1/x))^(10) +3x(x+(1/x))^(10) +10x^2 (x+(1/x))^(10) The term containing x^4 =The term containing x^4 in (x+(1/x))^(10) +The term containing x^4 in 3x(x+(1/x))^(10) +The term containing x^4 in 10x^2 (x+(1/x))^(10) T_(r+1) = ((n),(r) ) a^(n−r) b^r The term containing x^4 in (x+(1/x))^(10) T_(r+1) = (((10)),(( r)) ) (x)^(10−r) ((1/x))^r = (((10)),(( r)) ) (x)^(10−2r) 10−2r=4⇒r=3 T_(3+1) =T_4 = (((10)),(( 3)) ) x^4 =120x^4 ...(i) The term containing x^4 in 3x(x+(1/x))^(10) T_(r+1) =3x (((10)),(( r)) ) (x)^(10−r) ((1/x))^r T_(r+1) =3 (((10)),(( r)) ) (x)^(10−2r+1) 11−2r=4 r=7/2 As r may not be fraction hence there′s no term of x^4 in 3x(x+(1/x))^(10) ....(ii) The term containing x^4 in 10x^2 (x+(1/x))^(10) T_(r+1) =10x^2 (((10)),(( r)) ) (x)^(10−r) ((1/x))^r =10 (((10)),(( r)) ) (x)^(10−2r+2) 12−2r=4⇒r=4 T_(4+1) =T_5 =10 (((10)),(( 4)) ) x^4 =2100x^4 ..(iii) From (i) ,(ii) & (iii) 120x^4 +2100x^4 =2220x^4
$$\:\left(\mathrm{1}+\mathrm{3}\boldsymbol{\mathrm{x}}+\mathrm{10}\boldsymbol{\mathrm{x}}^{\mathrm{2}} \right)\left(\boldsymbol{\mathrm{x}}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}\right)^{\mathrm{10}} \\ $$$$=\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{10}} +\mathrm{3x}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{10}} +\mathrm{10x}^{\mathrm{2}} \left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{10}} \\ $$$$\mathrm{The}\:\mathrm{term}\:\mathrm{containing}\:\mathrm{x}^{\mathrm{4}} \\ $$$$\:\:\:=\mathrm{The}\:\mathrm{term}\:\mathrm{containing}\:\mathrm{x}^{\mathrm{4}} \:\mathrm{in}\:\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{10}} \\ $$$$\:\:\:\:\:\:\:+\mathrm{The}\:\mathrm{term}\:\mathrm{containing}\:\mathrm{x}^{\mathrm{4}} \:\mathrm{in}\:\mathrm{3x}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{10}} \\ $$$$\:\:\:\:\:\:\:+\mathrm{The}\:\mathrm{term}\:\mathrm{containing}\:\mathrm{x}^{\mathrm{4}} \:\mathrm{in}\:\mathrm{10x}^{\mathrm{2}} \left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{10}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{T}_{\mathrm{r}+\mathrm{1}} =\begin{pmatrix}{\mathrm{n}}\\{\mathrm{r}}\end{pmatrix}\:\mathrm{a}^{\mathrm{n}−\mathrm{r}} \mathrm{b}^{\mathrm{r}} \\ $$$$\:\mathrm{The}\:\mathrm{term}\:\mathrm{containing}\:\mathrm{x}^{\mathrm{4}} \:\mathrm{in}\:\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{10}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{T}_{\mathrm{r}+\mathrm{1}} =\begin{pmatrix}{\mathrm{10}}\\{\:\:\mathrm{r}}\end{pmatrix}\:\left(\mathrm{x}\right)^{\mathrm{10}−\mathrm{r}} \left(\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{r}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\begin{pmatrix}{\mathrm{10}}\\{\:\:\mathrm{r}}\end{pmatrix}\:\left(\mathrm{x}\right)^{\mathrm{10}−\mathrm{2r}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{10}−\mathrm{2r}=\mathrm{4}\Rightarrow\mathrm{r}=\mathrm{3} \\ $$$$\:\:\:\:\mathrm{T}_{\mathrm{3}+\mathrm{1}} =\mathrm{T}_{\mathrm{4}} =\begin{pmatrix}{\mathrm{10}}\\{\:\:\mathrm{3}}\end{pmatrix}\:\mathrm{x}^{\mathrm{4}} =\mathrm{120}\boldsymbol{\mathrm{x}}^{\mathrm{4}} …\left(\mathrm{i}\right) \\ $$$$\mathrm{The}\:\mathrm{term}\:\mathrm{containing}\:\mathrm{x}^{\mathrm{4}} \:\mathrm{in}\:\mathrm{3x}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{10}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{T}_{\mathrm{r}+\mathrm{1}} =\mathrm{3x}\begin{pmatrix}{\mathrm{10}}\\{\:\:\mathrm{r}}\end{pmatrix}\:\left(\mathrm{x}\right)^{\mathrm{10}−\mathrm{r}} \left(\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{r}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{T}_{\mathrm{r}+\mathrm{1}} =\mathrm{3}\begin{pmatrix}{\mathrm{10}}\\{\:\:\mathrm{r}}\end{pmatrix}\:\left(\mathrm{x}\right)^{\mathrm{10}−\mathrm{2r}+\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{11}−\mathrm{2r}=\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{r}=\mathrm{7}/\mathrm{2}\: \\ $$$$\mathrm{As}\:\mathrm{r}\:\mathrm{may}\:\mathrm{not}\:\mathrm{be}\:\mathrm{fraction}\:\mathrm{hence} \\ $$$$\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{term}\:\mathrm{of}\:\mathrm{x}^{\mathrm{4}} \mathrm{in}\:\mathrm{3x}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{10}} ….\left(\mathrm{ii}\right) \\ $$$$\mathrm{The}\:\mathrm{term}\:\mathrm{containing}\:\mathrm{x}^{\mathrm{4}} \:\mathrm{in}\:\mathrm{10x}^{\mathrm{2}} \left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{10}} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{T}_{\mathrm{r}+\mathrm{1}} =\mathrm{10x}^{\mathrm{2}} \begin{pmatrix}{\mathrm{10}}\\{\:\:\mathrm{r}}\end{pmatrix}\:\left(\mathrm{x}\right)^{\mathrm{10}−\mathrm{r}} \left(\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{r}} \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{10}\begin{pmatrix}{\mathrm{10}}\\{\:\:\mathrm{r}}\end{pmatrix}\:\left(\mathrm{x}\right)^{\mathrm{10}−\mathrm{2r}+\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{12}−\mathrm{2r}=\mathrm{4}\Rightarrow\mathrm{r}=\mathrm{4} \\ $$$$\:\:\:\:\:\:\mathrm{T}_{\mathrm{4}+\mathrm{1}} =\mathrm{T}_{\mathrm{5}} =\mathrm{10}\begin{pmatrix}{\mathrm{10}}\\{\:\mathrm{4}}\end{pmatrix}\:\mathrm{x}^{\mathrm{4}} =\mathrm{2100x}^{\mathrm{4}} ..\left(\mathrm{iii}\right) \\ $$$$ \\ $$$$\mathrm{From}\:\left(\mathrm{i}\right)\:,\left(\mathrm{ii}\right)\:\&\:\left(\mathrm{iii}\right) \\ $$$$\:\:\:\:\:\:\:\mathrm{120}\boldsymbol{\mathrm{x}}^{\mathrm{4}} +\mathrm{2100x}^{\mathrm{4}} =\mathrm{2220x}^{\mathrm{4}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *