Question Number 147528 by alcohol last updated on 21/Jul/21
![q_n =Π_(n=0) ^∞ cos((x/2^n )) i) study the variation of q_n ii) show that cosx=((sin2x)/(2sinx)) , ∀x∈[0,(π/2)] iii) deduce that q_n =(1/2^(n+1) )×((sin2x)/(sin((x/2^n )))) iv)lim_(n→∞) q_n =? v) solve cos((x/2))≥−(1/2)](https://www.tinkutara.com/question/Q147528.png)
$${q}_{{n}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\prod}}{cos}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right) \\ $$$$\left.{i}\right)\:{study}\:{the}\:{variation}\:{of}\:{q}_{{n}} \\ $$$$\left.{ii}\right) \\ $$$$\:{show}\:{that}\:{cosx}=\frac{{sin}\mathrm{2}{x}}{\mathrm{2}{sinx}}\:,\:\forall{x}\in\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\right] \\ $$$$\left.{iii}\right) \\ $$$${deduce}\:{that}\:{q}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} }×\frac{{sin}\mathrm{2}{x}}{{sin}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)} \\ $$$$\left.{iv}\right)\underset{{n}\rightarrow\infty} {\mathrm{lim}}{q}_{{n}} =? \\ $$$$\left.{v}\right)\: \\ $$$${solve}\:{cos}\left(\frac{{x}}{\mathrm{2}}\right)\geqslant−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Olaf_Thorendsen last updated on 21/Jul/21
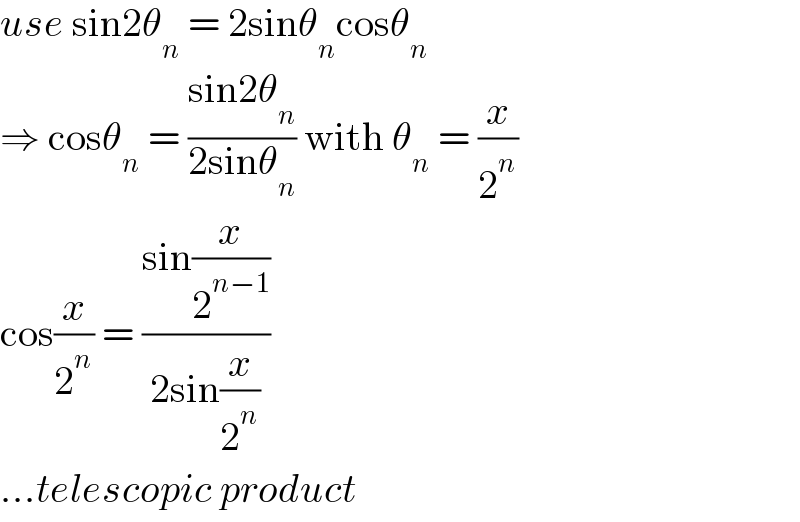
$${use}\:\mathrm{sin2}\theta_{{n}} \:=\:\mathrm{2sin}\theta_{{n}} \mathrm{cos}\theta_{{n}} \\ $$$$\Rightarrow\:\mathrm{cos}\theta_{{n}} \:=\:\frac{\mathrm{sin2}\theta_{{n}} }{\mathrm{2sin}\theta_{{n}} }\:\mathrm{with}\:\theta_{{n}} \:=\:\frac{{x}}{\mathrm{2}^{{n}} } \\ $$$$\mathrm{cos}\frac{{x}}{\mathrm{2}^{{n}} }\:=\:\frac{\mathrm{sin}\frac{{x}}{\mathrm{2}^{{n}−\mathrm{1}} }}{\mathrm{2sin}\frac{{x}}{\mathrm{2}^{{n}} }} \\ $$$$…{telescopic}\:{product} \\ $$
Commented by alcohol last updated on 21/Jul/21
$${thanks} \\ $$$${but}\:{i}\:{dont}\:{understand} \\ $$
Commented by puissant last updated on 21/Jul/21

$$\mathrm{U}_{\mathrm{n}} =\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\prod}}\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}^{\mathrm{k}} }\right)… \\ $$
