Question Number 25088 by naziri2013 last updated on 03/Dec/17

$$ \\ $$$$ \\ $$$$ \\ $$$${Q}…\frac{{x}+\mathrm{7}}{{x}+\mathrm{4}}>\mathrm{1},\:\:\:\:\:{x}\in{R} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by moxhix last updated on 03/Dec/17
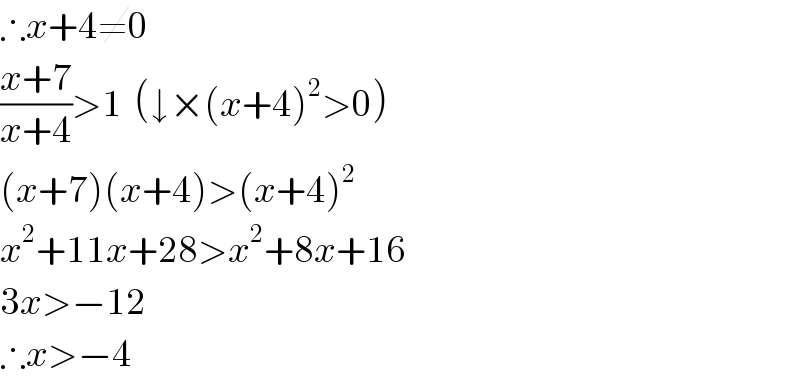
$$\therefore{x}+\mathrm{4}\neq\mathrm{0} \\ $$$$\frac{{x}+\mathrm{7}}{{x}+\mathrm{4}}>\mathrm{1}\:\:\left(\downarrow×\left({x}+\mathrm{4}\right)^{\mathrm{2}} >\mathrm{0}\right) \\ $$$$\left({x}+\mathrm{7}\right)\left({x}+\mathrm{4}\right)>\left({x}+\mathrm{4}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\mathrm{11}{x}+\mathrm{28}>{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{16} \\ $$$$\mathrm{3}{x}>−\mathrm{12} \\ $$$$\therefore{x}>−\mathrm{4} \\ $$
Answered by Rasheed.Sindhi last updated on 04/Dec/17
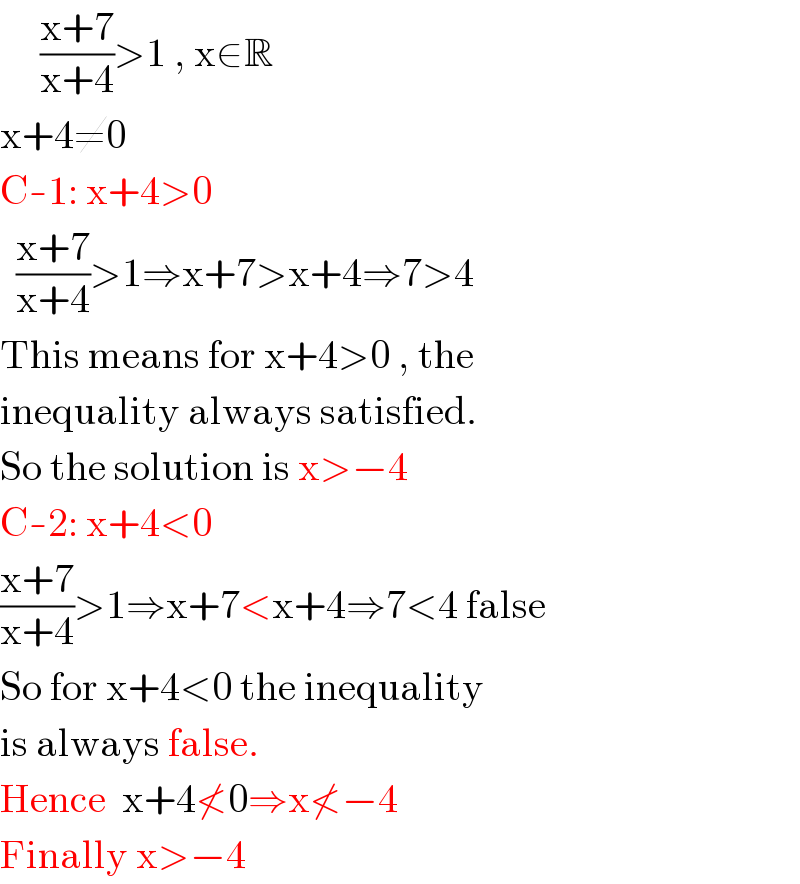
$$\:\:\:\:\:\frac{\mathrm{x}+\mathrm{7}}{\mathrm{x}+\mathrm{4}}>\mathrm{1}\:,\:\mathrm{x}\in\mathbb{R} \\ $$$$\mathrm{x}+\mathrm{4}\neq\mathrm{0} \\ $$$$\mathrm{C}-\mathrm{1}:\:\mathrm{x}+\mathrm{4}>\mathrm{0} \\ $$$$\:\:\frac{\mathrm{x}+\mathrm{7}}{\mathrm{x}+\mathrm{4}}>\mathrm{1}\Rightarrow\mathrm{x}+\mathrm{7}>\mathrm{x}+\mathrm{4}\Rightarrow\mathrm{7}>\mathrm{4} \\ $$$$\mathrm{This}\:\mathrm{means}\:\mathrm{for}\:\mathrm{x}+\mathrm{4}>\mathrm{0}\:,\:\mathrm{the} \\ $$$$\mathrm{inequality}\:\mathrm{always}\:\mathrm{satisfied}. \\ $$$$\mathrm{So}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{x}>−\mathrm{4} \\ $$$$\mathrm{C}-\mathrm{2}:\:\mathrm{x}+\mathrm{4}<\mathrm{0} \\ $$$$\frac{\mathrm{x}+\mathrm{7}}{\mathrm{x}+\mathrm{4}}>\mathrm{1}\Rightarrow\mathrm{x}+\mathrm{7}<\mathrm{x}+\mathrm{4}\Rightarrow\mathrm{7}<\mathrm{4}\:\mathrm{false} \\ $$$$\mathrm{So}\:\mathrm{for}\:\mathrm{x}+\mathrm{4}<\mathrm{0}\:\mathrm{the}\:\mathrm{inequality} \\ $$$$\mathrm{is}\:\mathrm{always}\:\mathrm{false}. \\ $$$$\mathrm{Hence}\:\:\mathrm{x}+\mathrm{4}\nless\mathrm{0}\Rightarrow\mathrm{x}\nless−\mathrm{4} \\ $$$$\mathrm{Finally}\:\mathrm{x}>−\mathrm{4} \\ $$
