Question Number 103492 by abony1303 last updated on 15/Jul/20

Commented by abony1303 last updated on 15/Jul/20

Answered by mr W last updated on 15/Jul/20

Commented by abony1303 last updated on 15/Jul/20

Commented by mr W last updated on 15/Jul/20

Commented by mr W last updated on 15/Jul/20
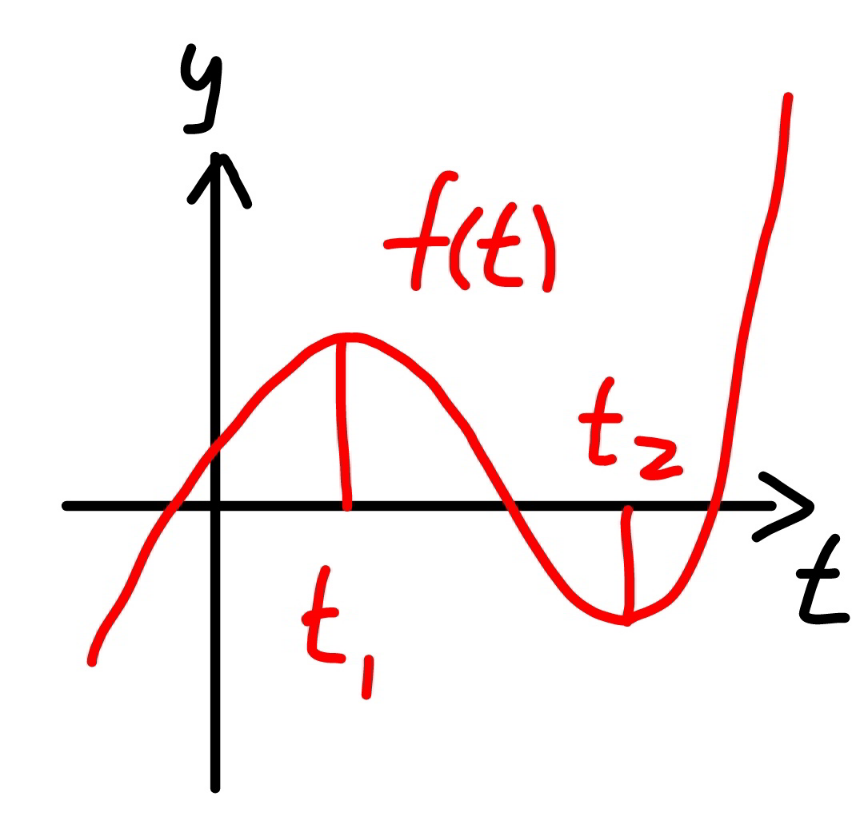
Commented by mr W last updated on 15/Jul/20
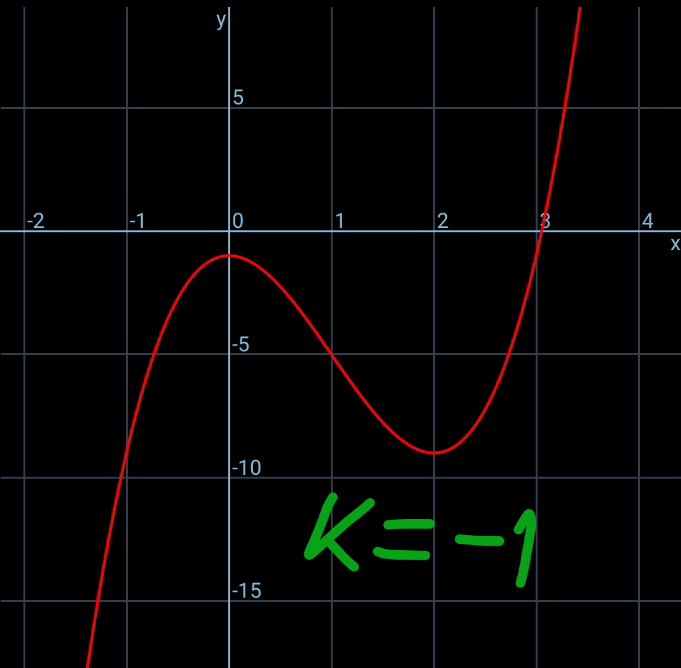
Commented by mr W last updated on 15/Jul/20
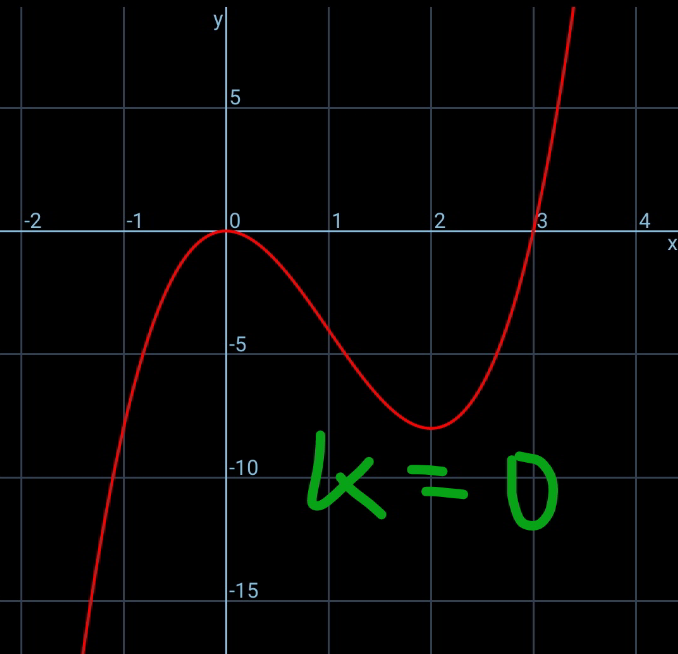
Commented by mr W last updated on 15/Jul/20

Commented by mr W last updated on 15/Jul/20

Commented by mr W last updated on 15/Jul/20

Commented by mr W last updated on 15/Jul/20

Answered by mr W last updated on 15/Jul/20

Answered by mr W last updated on 15/Jul/20

Answered by OlafThorendsen last updated on 15/Jul/20
![Q1. I = ∫_(−1) ^1 ∣x∣(x^3 +1)dx I = ∫_(−1) ^0 −x(x^3 +1)dx+∫_0 ^1 x(x^3 +1)dx I = [−(x^5 /5)−(x^2 /2)]_(−1) ^0 +[(x^5 /5)+(x^2 /2)]_0 ^1 I = (−(1/5)+(1/2))+((1/5)+(1/2)) I = 1 Q2. Δ′ = (−3)^2 −(2)(k) = 9−2k More than one solution ⇔ Δ′>0 ⇔ k<(9/2) ⇔ k∈{0;1;2;3;4} ⇒ sum = 0+1+2+3+4 = 10 Q3. A is a point of the curve B is a point of the line A ((a),((a^2 −a)) ) and B ((b),((b−3)) ) AB^2 = (b−a)^2 +(b−3−a^2 +a)^2 for a given a, AB^2 = f(b) f(b) = (b−a)^2 +(b−3−a^2 +a)^2 f′(b) = 2(b−a)+2(b−3−a^2 +a) f′(b) = 4b−2a^2 −6 f′(b) = 0 ⇔ b = ((a^2 +3)/2) Then : AB^2 = (((a^2 +3)/2)−a)^2 +(((a^2 +3)/2)−3−a^2 +a)^2 AB^2 = ((a^2 /2)−a+(3/2))^2 +(−(a^2 /2)+a−(3/2))^2 AB^2 = 2((a^2 /2)−a+(3/2))^2 AB = (√2)∣(a^2 /2)−a+(3/2)∣ and then : A ((a),((a^2 −a)) ) and B ((((a^2 +3)/2)),(((a^2 −3)/2)) )](https://www.tinkutara.com/question/Q103501.png)
Commented by abony1303 last updated on 15/Jul/20

Commented by OlafThorendsen last updated on 15/Jul/20

Commented by abony1303 last updated on 15/Jul/20

Commented by bemath last updated on 15/Jul/20

Commented by abony1303 last updated on 15/Jul/20

Commented by OlafThorendsen last updated on 15/Jul/20

Commented by abony1303 last updated on 15/Jul/20

