Question Number 108914 by 1549442205PVT last updated on 21/Aug/20
![Q108815(19/8/20)(unanswer)by 1x.x Given f(x)=(1/( (√(1+x))))+(1/( (√(1+a))))+((√(ax))/( (√(ax+8)))) x,a∈R;x,a>0.Prove that 1<f(x)<2 Solution:Put x=tan^2 A,a=tan^2 B(A,B∈[0,(π/2)) f(x)=cosA+cosB+((tanAtanB)/( (√(tan^2 Atan^2 B+8)))) =cosA+cosB+((sinAsinB)/( (√(8cos^2 Acos^2 B+sin^2 Asin^2 B)))) Put cosA=z,cosB=y(z,y∈(0,1])we have f=z+y+((√((1−z^2 )(1−y^2 )))/( (√(8z^2 y^2 +(1−z^2 )(1−y^2 ))))) =z+y+((√((1−z^2 )(1−y^2 )))/( (√(9z^2 y^2 +1−(z^2 +y^2 ))))) i)First we prove f(x)>1 ⇔z+y+((√((1−z^2 )(1− y^2 )))/( (√(9z^2 y^2 +1−(z^2 +y^2 )))))>1(1) If z+y≥1 then the inequality(1) is true.Consider z+y<1.Put m=1−(z+y)⇔z+y=1−m(0<m≤1) z^2 +y^2 =(z+y)^2 −2zy=(1−m)^2 −2zy (1)⇔(((1−z^2 )(1−y^2 ))/( 9z^2 y^2 +1−(z^2 +y^2 )))>[1−(z+y)]^2 ⇔1+z^2 y^2 −(z^2 +y^2 )>[9z^2 y^2 +1−(z^2 +y^2 )]m^2 1+z^2 y^2 −[1−2m+m^2 −2zy]>[9z^2 y^2 +1−(1−2m+m^2 −2zy)]m^2 ⇔z^2 y^2 +2zy+2m−m^2 >(9z^2 y^2 +2zy+2m−m^2 )m^2 ⇔m^4 −m^2 (9z^2 y^2 +2zy+2m)+(z^2 y^2 +2zy+2m−m^2 )>0 We look at LHS as a quadratic polynomial with respect to “im^2 ” defined on the interval(0;1) and we denote by P(m).By the theorem above the sign of quadratic poly.P(m)>0⇔ Δ_P =(9z^2 y^2 +2zy+2m)^2 −4(z^2 y^2 +2zy+2m−m^2 )<0 ⇔81z^4 y^4 +4z^2 y^2 +4m^2 +36z^3 y^3 +36mz^2 y^2 +8mzy−4(z^2 y^2 +2zy+2m−m^2 )<0 ⇔81z^4 y^4 +36z^3 y^3 +36mz^2 y^2 +8(m−1)zy+8m^2 −8m<0 ⇔8m^2 +(36z^2 y^2 +8zy−8)m+81z^4 y^4 +36z^3 y^3 −8zy<0(3) We look at LHS (3) like as a quadratic polynomial w.r.t “m” and denote by Q(m) We has Q(0)=81(zy)^4 +36(zy)^3 −8zy ≤81t/64+36t/16−8t=225t/64−8t<0 (due to 0< t=zy≤1/4 ) Q(1)=1+36(zy)^2 +8zy−8+81(zy)^4 +36(zy)^3 −8zy =−7+36(zy)^2 +81(zy)^4 +36(zy)^3 ≤ −7+36/16+81/256+36/64<0 (due to zy≤1/4) By the convert theorem above the sign of the quadratic polynomial we infer Q(m)>0 ∀m∈(0;1)which means P(m) has Δ_P <0 ∀m∈(0;1)⇒the inequality (1) proved ii)Now we prove that f(x)<2 ⇔z+y+((√((1−z^2 )(1−y^2 )))/( (√(9z^2 y^2 +1−(z^2 +y^2 )))))<2(4) ⇔(((1−z^2 )(1−y^2 ))/(9z^2 y^2 +1−(z^2 +y^2 )))<[2−(z+y)]^2 ⇔1+z^2 y^2 −(z^2 +y^2 )<[9z^2 y^2 +1−(z^2 +y^2 )](1+m)^2 (note (1−m=z+y like as above we have −1≤m=1−(z+y)<1 as 0<z+y≤2(∗)) ⇔z^2 y^2 +2zy+2m−m^2 <(9z^2 y^2 +2zy+2m−m^2 )(1+2m+m^2 ) ⇔z^2 y^2 +2zy+2m−m^2 <(9z^2 y^2 +2zy+2m−m^2 )+(9z^2 y^2 +2zy)(2m+m^2 )−m^4 +4m^2 >0 ⇔−m^4 +4m^2 +(9z^2 y^2 +2zy)(2m+m^2 )+8z^2 y^2 >0 ⇔(9m^2 +18m+8)(zy)^2 +2(m^2 +2m)zy−m^4 +4m^2 >0(4) We look at LHS like as a quadratic polynomial w.r.t “zy” and denote by H(t)(set t=zy,0<zy≤(((z+y)/2))≤1) a)The case 9m^2 +18m+8>0 We consider the discriminant Δ_H ′of H(t) Δ_H ′=(m^2 +2m)^2 +(9m^2 +18m+8)(m^4 −4m^2 ) =m^4 +4m^3 +4m^2 +9m^6 +18m^5 −28m^4 −72m^3 −32m^2 =9m^6 +18m^5 −27m^4 −68m^3 −28m^2 =m^2 (9m^4 +18m^3 −27m^2 −68m−28) <0( due to ∣m∣≤1). Therefore,we infer H(t)>0∀t∈(0;1]which means the inequality (4)is proved ,so f(x)<2 b)The case 9m^2 +18m+8 < 0 ⇔−1<m<−2/3 .We have { ((H(0)=−m^4 +4m^2 =m^2 (4−m^2 )>0 )),((H(1)=−m^4 +15m^2 +22m+8=)),(((1+m)(−m^3 +m^2 +14m+8)>0)) :} By the convert theorem above the sign of the quadratic polynomial we infer H(t)>0 ∀t=zy∈(0;1)⇒(4)is proved which means we ger f(2)<2 other way: Similar to the case i)Rewrite H(t) in the form H(m^2 )as the quadratic poly. w.r.t “m^2 ” with the highest efficient k=(−1)we get H(0)>0,H(1)>0 ⇒kH(0)<0,kH(1)<0⇒H(m)>0 ∀m^2 ∈[0,1]⇔m∈[−1,1] From i)and ii)we obtain 1<f(x)<2(q.e.d)](https://www.tinkutara.com/question/Q108914.png)
$$ \\ $$$$\mathrm{Q108815}\left(\mathrm{19}/\mathrm{8}/\mathrm{20}\right)\left(\mathrm{unanswer}\right)\mathrm{by}\:\mathrm{1x}.\mathrm{x} \\ $$$$\mathrm{Given}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{x}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{a}}}+\frac{\sqrt{\mathrm{ax}}}{\:\sqrt{\mathrm{ax}+\mathrm{8}}} \\ $$$$\mathrm{x},\mathrm{a}\in\mathrm{R};\mathrm{x},\mathrm{a}>\mathrm{0}.\mathrm{Prove}\:\mathrm{that} \\ $$$$\mathrm{1}<\mathrm{f}\left(\mathrm{x}\right)<\mathrm{2} \\ $$$$\mathrm{Solution}:\mathrm{Put}\:\mathrm{x}=\mathrm{tan}^{\mathrm{2}} \mathrm{A},\mathrm{a}=\mathrm{tan}^{\mathrm{2}} \mathrm{B}\left(\mathrm{A},\mathrm{B}\in\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\right)\right. \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{cosA}+\mathrm{cosB}+\frac{\mathrm{tanAtanB}}{\:\sqrt{\mathrm{tan}^{\mathrm{2}} \mathrm{Atan}^{\mathrm{2}} \mathrm{B}+\mathrm{8}}} \\ $$$$=\mathrm{cosA}+\mathrm{cosB}+\frac{\mathrm{sinAsinB}}{\:\sqrt{\mathrm{8cos}^{\mathrm{2}} \mathrm{Acos}^{\mathrm{2}} \mathrm{B}+\mathrm{sin}^{\mathrm{2}} \mathrm{Asin}^{\mathrm{2}} \mathrm{B}}} \\ $$$$\mathrm{Put}\:\mathrm{cosA}=\mathrm{z},\mathrm{cosB}=\mathrm{y}\left(\mathrm{z},\mathrm{y}\in\left(\mathrm{0},\mathrm{1}\right]\right)\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{f}=\mathrm{z}+\mathrm{y}+\frac{\sqrt{\left(\mathrm{1}−\mathrm{z}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{y}^{\mathrm{2}} \right)}}{\:\sqrt{\mathrm{8z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\left(\mathrm{1}−\mathrm{z}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{y}^{\mathrm{2}} \right)}} \\ $$$$=\mathrm{z}+\mathrm{y}+\frac{\sqrt{\left(\mathrm{1}−\mathrm{z}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{y}^{\mathrm{2}} \right)}}{\:\sqrt{\mathrm{9z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{1}−\left(\mathrm{z}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)}} \\ $$$$\left.\boldsymbol{\mathrm{i}}\right)\boldsymbol{\mathrm{First}}\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)>\mathrm{1} \\ $$$$\Leftrightarrow\mathrm{z}+\mathrm{y}+\frac{\sqrt{\left(\mathrm{1}−\mathrm{z}^{\mathrm{2}} \right)\left(\mathrm{1}−\:\mathrm{y}^{\mathrm{2}} \right)}}{\:\sqrt{\mathrm{9z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{1}−\left(\mathrm{z}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)}}>\mathrm{1}\left(\mathrm{1}\right) \\ $$$$\mathrm{If}\:\mathrm{z}+\mathrm{y}\geqslant\mathrm{1}\:\mathrm{then}\:\mathrm{the}\:\mathrm{inequality}\left(\mathrm{1}\right)\:\mathrm{is} \\ $$$$\mathrm{true}.\mathrm{Consider}\:\mathrm{z}+\mathrm{y}<\mathrm{1}.\mathrm{Put} \\ $$$$\mathrm{m}=\mathrm{1}−\left(\mathrm{z}+\mathrm{y}\right)\Leftrightarrow\mathrm{z}+\mathrm{y}=\mathrm{1}−\mathrm{m}\left(\mathrm{0}<\mathrm{m}\leqslant\mathrm{1}\right) \\ $$$$\mathrm{z}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\left(\mathrm{z}+\mathrm{y}\right)^{\mathrm{2}} −\mathrm{2zy}=\left(\mathrm{1}−\mathrm{m}\right)^{\mathrm{2}} −\mathrm{2zy} \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow\frac{\left(\mathrm{1}−\mathrm{z}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{y}^{\mathrm{2}} \right)}{\:\:\:\mathrm{9z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{1}−\left(\mathrm{z}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)}>\left[\mathrm{1}−\left(\mathrm{z}+\mathrm{y}\right)\right]^{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{1}+\mathrm{z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} −\left(\mathrm{z}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)>\left[\mathrm{9z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{1}−\left(\mathrm{z}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)\right]\mathrm{m}^{\mathrm{2}} \\ $$$$\mathrm{1}+\mathrm{z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} −\left[\mathrm{1}−\mathrm{2m}+\mathrm{m}^{\mathrm{2}} −\mathrm{2zy}\right]>\left[\mathrm{9z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{1}−\left(\mathrm{1}−\mathrm{2m}+\mathrm{m}^{\mathrm{2}} −\mathrm{2zy}\right)\right]\mathrm{m}^{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{2zy}+\mathrm{2m}−\mathrm{m}^{\mathrm{2}} >\left(\mathrm{9z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{2zy}+\mathrm{2m}−\mathrm{m}^{\mathrm{2}} \right)\mathrm{m}^{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{m}^{\mathrm{4}} −\mathrm{m}^{\mathrm{2}} \left(\mathrm{9z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{2zy}+\mathrm{2m}\right)+\left(\mathrm{z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{2zy}+\mathrm{2m}−\mathrm{m}^{\mathrm{2}} \right)>\mathrm{0} \\ $$$$\mathrm{We}\:\mathrm{look}\:\mathrm{at}\:\mathrm{LHS}\:\mathrm{as}\:\mathrm{a}\:\mathrm{quadratic}\:\mathrm{polynomial} \\ $$$$\mathrm{with}\:\mathrm{respect}\:\mathrm{to}\:“\mathrm{im}^{\mathrm{2}} ''\:\mathrm{defined}\:\mathrm{on}\:\mathrm{the}\:\mathrm{interval}\left(\mathrm{0};\mathrm{1}\right) \\ $$$$\:\mathrm{and}\:\mathrm{we}\:\mathrm{denote}\:\mathrm{by}\:\mathrm{P}\left(\mathrm{m}\right).\mathrm{By}\:\mathrm{the}\:\mathrm{theorem} \\ $$$$\mathrm{above}\:\mathrm{the}\:\mathrm{sign}\:\mathrm{of}\:\mathrm{quadratic}\:\mathrm{poly}.\mathrm{P}\left(\mathrm{m}\right)>\mathrm{0}\Leftrightarrow \\ $$$$\:\Delta_{\mathrm{P}} =\left(\mathrm{9z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{2zy}+\mathrm{2m}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{2zy}+\mathrm{2m}−\mathrm{m}^{\mathrm{2}} \right)<\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{81z}^{\mathrm{4}} \mathrm{y}^{\mathrm{4}} +\mathrm{4z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{4m}^{\mathrm{2}} +\mathrm{36z}^{\mathrm{3}} \mathrm{y}^{\mathrm{3}} +\mathrm{36mz}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{8mzy}−\mathrm{4}\left(\mathrm{z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{2zy}+\mathrm{2m}−\mathrm{m}^{\mathrm{2}} \right)<\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{81z}^{\mathrm{4}} \mathrm{y}^{\mathrm{4}} +\mathrm{36z}^{\mathrm{3}} \mathrm{y}^{\mathrm{3}} +\mathrm{36mz}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{8}\left(\mathrm{m}−\mathrm{1}\right)\mathrm{zy}+\mathrm{8m}^{\mathrm{2}} −\mathrm{8m}<\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{8m}^{\mathrm{2}} +\left(\mathrm{36z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{8zy}−\mathrm{8}\right)\mathrm{m}+\mathrm{81z}^{\mathrm{4}} \mathrm{y}^{\mathrm{4}} +\mathrm{36z}^{\mathrm{3}} \mathrm{y}^{\mathrm{3}} −\mathrm{8zy}<\mathrm{0}\left(\mathrm{3}\right) \\ $$$$\mathrm{We}\:\mathrm{look}\:\mathrm{at}\:\mathrm{LHS}\:\left(\mathrm{3}\right)\:\mathrm{like}\:\mathrm{as}\:\mathrm{a}\:\mathrm{quadratic} \\ $$$$\mathrm{polynomial}\:\mathrm{w}.\mathrm{r}.\mathrm{t}\:“\mathrm{m}''\:\mathrm{and}\:\mathrm{denote}\:\mathrm{by}\:\mathrm{Q}\left(\mathrm{m}\right) \\ $$$$\mathrm{We}\:\mathrm{has}\:\mathrm{Q}\left(\mathrm{0}\right)=\mathrm{81}\left(\mathrm{zy}\right)^{\mathrm{4}} +\mathrm{36}\left(\mathrm{zy}\right)^{\mathrm{3}} −\mathrm{8zy} \\ $$$$\leqslant\mathrm{81t}/\mathrm{64}+\mathrm{36t}/\mathrm{16}−\mathrm{8t}=\mathrm{225t}/\mathrm{64}−\mathrm{8t}<\mathrm{0} \\ $$$$\left(\mathrm{due}\:\mathrm{to}\:\mathrm{0}<\:\mathrm{t}=\mathrm{zy}\leqslant\mathrm{1}/\mathrm{4}\:\right) \\ $$$$\mathrm{Q}\left(\mathrm{1}\right)=\mathrm{1}+\mathrm{36}\left(\mathrm{zy}\right)^{\mathrm{2}} +\mathrm{8zy}−\mathrm{8}+\mathrm{81}\left(\mathrm{zy}\right)^{\mathrm{4}} +\mathrm{36}\left(\mathrm{zy}\right)^{\mathrm{3}} −\mathrm{8zy} \\ $$$$=−\mathrm{7}+\mathrm{36}\left(\mathrm{zy}\right)^{\mathrm{2}} +\mathrm{81}\left(\mathrm{zy}\right)^{\mathrm{4}} +\mathrm{36}\left(\mathrm{zy}\right)^{\mathrm{3}} \leqslant \\ $$$$−\mathrm{7}+\mathrm{36}/\mathrm{16}+\mathrm{81}/\mathrm{256}+\mathrm{36}/\mathrm{64}<\mathrm{0}\:\left(\mathrm{due}\:\mathrm{to}\:\mathrm{zy}\leqslant\mathrm{1}/\mathrm{4}\right) \\ $$$$\mathrm{By}\:\mathrm{the}\:\mathrm{convert}\:\mathrm{theorem}\:\mathrm{above}\:\mathrm{the}\:\mathrm{sign} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{quadratic}\:\mathrm{polynomial}\:\mathrm{we}\:\mathrm{infer} \\ $$$$\mathrm{Q}\left(\mathrm{m}\right)>\mathrm{0}\:\forall\mathrm{m}\in\left(\mathrm{0};\mathrm{1}\right)\mathrm{which}\:\mathrm{means}\:\mathrm{P}\left(\mathrm{m}\right) \\ $$$$\mathrm{has}\:\Delta_{\mathrm{P}} <\mathrm{0}\:\forall\mathrm{m}\in\left(\mathrm{0};\mathrm{1}\right)\Rightarrow\mathrm{the}\:\mathrm{inequality}\:\left(\mathrm{1}\right)\: \\ $$$$\mathrm{proved} \\ $$$$\left.\boldsymbol{\mathrm{ii}}\right)\boldsymbol{\mathrm{Now}}\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{that}}\:\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)<\mathrm{2} \\ $$$$\Leftrightarrow\mathrm{z}+\mathrm{y}+\frac{\sqrt{\left(\mathrm{1}−\mathrm{z}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{y}^{\mathrm{2}} \right)}}{\:\sqrt{\mathrm{9z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{1}−\left(\mathrm{z}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)}}<\mathrm{2}\left(\mathrm{4}\right) \\ $$$$\Leftrightarrow\frac{\left(\mathrm{1}−\mathrm{z}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{y}^{\mathrm{2}} \right)}{\mathrm{9z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{1}−\left(\mathrm{z}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)}<\left[\mathrm{2}−\left(\mathrm{z}+\mathrm{y}\right)\right]^{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{1}+\mathrm{z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} −\left(\mathrm{z}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)<\left[\mathrm{9z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{1}−\left(\mathrm{z}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)\right]\left(\mathrm{1}+\mathrm{m}\right)^{\mathrm{2}} \left(\mathrm{note}\right. \\ $$$$\left(\mathrm{1}−\mathrm{m}=\mathrm{z}+\mathrm{y}\:\mathrm{like}\:\mathrm{as}\:\mathrm{above}\:\mathrm{we}\:\mathrm{have}\right. \\ $$$$\left.−\mathrm{1}\leqslant\mathrm{m}=\mathrm{1}−\left(\mathrm{z}+\mathrm{y}\right)<\mathrm{1}\:\mathrm{as}\:\mathrm{0}<\mathrm{z}+\mathrm{y}\leqslant\mathrm{2}\left(\ast\right)\right) \\ $$$$\Leftrightarrow\mathrm{z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{2zy}+\mathrm{2m}−\mathrm{m}^{\mathrm{2}} <\left(\mathrm{9z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{2zy}+\mathrm{2m}−\mathrm{m}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{2m}+\mathrm{m}^{\mathrm{2}} \right) \\ $$$$\Leftrightarrow\mathrm{z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{2zy}+\mathrm{2m}−\mathrm{m}^{\mathrm{2}} <\left(\mathrm{9z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{2zy}+\mathrm{2m}−\mathrm{m}^{\mathrm{2}} \right)+\left(\mathrm{9z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{2zy}\right)\left(\mathrm{2m}+\mathrm{m}^{\mathrm{2}} \right)−\mathrm{m}^{\mathrm{4}} +\mathrm{4m}^{\mathrm{2}} >\mathrm{0} \\ $$$$\Leftrightarrow−\mathrm{m}^{\mathrm{4}} +\mathrm{4m}^{\mathrm{2}} +\left(\mathrm{9z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{2zy}\right)\left(\mathrm{2m}+\mathrm{m}^{\mathrm{2}} \right)+\mathrm{8z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} >\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{9m}^{\mathrm{2}} +\mathrm{18m}+\mathrm{8}\right)\left(\mathrm{zy}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{m}^{\mathrm{2}} +\mathrm{2m}\right)\mathrm{zy}−\mathrm{m}^{\mathrm{4}} +\mathrm{4m}^{\mathrm{2}} >\mathrm{0}\left(\mathrm{4}\right) \\ $$$$\mathrm{We}\:\mathrm{look}\:\mathrm{at}\:\:\mathrm{LHS}\:\mathrm{like}\:\mathrm{as}\:\mathrm{a}\:\mathrm{quadratic} \\ $$$$\mathrm{polynomial}\:\mathrm{w}.\mathrm{r}.\mathrm{t}\:“\mathrm{zy}''\:\mathrm{and}\:\mathrm{denote}\:\mathrm{by} \\ $$$$\mathrm{H}\left(\mathrm{t}\right)\left(\mathrm{set}\:\mathrm{t}=\mathrm{zy},\mathrm{0}<\mathrm{zy}\leqslant\left(\frac{\mathrm{z}+\mathrm{y}}{\mathrm{2}}\right)\leqslant\mathrm{1}\right) \\ $$$$\left.\boldsymbol{\mathrm{a}}\right)\boldsymbol{\mathrm{The}}\:\boldsymbol{\mathrm{case}}\:\:\mathrm{9}\boldsymbol{\mathrm{m}}^{\mathrm{2}} +\mathrm{18}\boldsymbol{\mathrm{m}}+\mathrm{8}>\mathrm{0}\: \\ $$$$\mathrm{We}\:\mathrm{consider}\:\mathrm{the}\:\mathrm{discriminant}\:\Delta_{\mathrm{H}} '\mathrm{of}\:\mathrm{H}\left(\mathrm{t}\right) \\ $$$$\Delta_{\mathrm{H}} '=\left(\mathrm{m}^{\mathrm{2}} +\mathrm{2m}\right)^{\mathrm{2}} +\left(\mathrm{9m}^{\mathrm{2}} +\mathrm{18m}+\mathrm{8}\right)\left(\mathrm{m}^{\mathrm{4}} −\mathrm{4m}^{\mathrm{2}} \right) \\ $$$$=\mathrm{m}^{\mathrm{4}} +\mathrm{4m}^{\mathrm{3}} +\mathrm{4m}^{\mathrm{2}} +\mathrm{9m}^{\mathrm{6}} +\mathrm{18m}^{\mathrm{5}} −\mathrm{28m}^{\mathrm{4}} −\mathrm{72m}^{\mathrm{3}} −\mathrm{32m}^{\mathrm{2}} \\ $$$$=\mathrm{9m}^{\mathrm{6}} +\mathrm{18m}^{\mathrm{5}} −\mathrm{27m}^{\mathrm{4}} −\mathrm{68m}^{\mathrm{3}} −\mathrm{28m}^{\mathrm{2}} \\ $$$$=\mathrm{m}^{\mathrm{2}} \left(\mathrm{9m}^{\mathrm{4}} +\mathrm{18m}^{\mathrm{3}} −\mathrm{27m}^{\mathrm{2}} −\mathrm{68m}−\mathrm{28}\right) \\ $$$$<\mathrm{0}\left(\:\boldsymbol{\mathrm{due}}\:\boldsymbol{\mathrm{to}}\:\mid\boldsymbol{\mathrm{m}}\mid\leqslant\mathrm{1}\right).\:\mathrm{Therefore},\mathrm{we}\: \\ $$$$\mathrm{infer}\:\mathrm{H}\left(\mathrm{t}\right)>\mathrm{0}\forall\mathrm{t}\in\left(\mathrm{0};\mathrm{1}\right]\mathrm{which}\:\mathrm{means} \\ $$$$\mathrm{the}\:\mathrm{inequality}\:\left(\mathrm{4}\right)\mathrm{is}\:\:\mathrm{proved}\:,\mathrm{so}\:\mathrm{f}\left(\mathrm{x}\right)<\mathrm{2} \\ $$$$\left.\boldsymbol{\mathrm{b}}\right)\boldsymbol{\mathrm{The}}\:\boldsymbol{\mathrm{case}}\:\:\mathrm{9}\boldsymbol{\mathrm{m}}^{\mathrm{2}} +\mathrm{18}\boldsymbol{\mathrm{m}}+\mathrm{8}\:<\:\mathrm{0}\: \\ $$$$\:\Leftrightarrow−\mathrm{1}<\boldsymbol{\mathrm{m}}<−\mathrm{2}/\mathrm{3}\:.\mathrm{We}\:\mathrm{have} \\ $$$$\begin{cases}{\mathrm{H}\left(\mathrm{0}\right)=−\mathrm{m}^{\mathrm{4}} +\mathrm{4m}^{\mathrm{2}} =\mathrm{m}^{\mathrm{2}} \left(\mathrm{4}−\mathrm{m}^{\mathrm{2}} \right)>\mathrm{0}\:}\\{\mathrm{H}\left(\mathrm{1}\right)=−\mathrm{m}^{\mathrm{4}} +\mathrm{15m}^{\mathrm{2}} +\mathrm{22m}+\mathrm{8}=}\\{\left(\mathrm{1}+\mathrm{m}\right)\left(−\mathrm{m}^{\mathrm{3}} +\mathrm{m}^{\mathrm{2}} +\mathrm{14m}+\mathrm{8}\right)>\mathrm{0}}\end{cases} \\ $$$$\mathrm{By}\:\mathrm{the}\:\mathrm{convert}\:\mathrm{theorem}\:\mathrm{above}\:\mathrm{the}\:\mathrm{sign} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{quadratic}\:\mathrm{polynomial}\:\mathrm{we}\:\mathrm{infer} \\ $$$$\mathrm{H}\left(\mathrm{t}\right)>\mathrm{0}\:\forall\mathrm{t}=\mathrm{zy}\in\left(\mathrm{0};\mathrm{1}\right)\Rightarrow\left(\mathrm{4}\right)\mathrm{is}\:\mathrm{proved} \\ $$$$\mathrm{which}\:\mathrm{means}\:\mathrm{we}\:\mathrm{ger}\:\mathrm{f}\left(\mathrm{2}\right)<\mathrm{2} \\ $$$$\boldsymbol{\mathrm{other}}\:\boldsymbol{\mathrm{way}}: \\ $$$$\left.\mathrm{Similar}\:\mathrm{to}\:\mathrm{the}\:\mathrm{case}\:\mathrm{i}\right)\mathrm{Rewrite}\:\mathrm{H}\left(\mathrm{t}\right)\:\mathrm{in}\: \\ $$$$\mathrm{the}\:\mathrm{form}\:\mathrm{H}\left(\mathrm{m}^{\mathrm{2}} \right)\mathrm{as}\:\mathrm{the}\:\mathrm{quadratic}\:\mathrm{poly}. \\ $$$$\mathrm{w}.\mathrm{r}.\mathrm{t}\:“\mathrm{m}^{\mathrm{2}} ''\:\mathrm{with}\:\mathrm{the}\:\mathrm{highest}\:\mathrm{efficient} \\ $$$$\mathrm{k}=\left(−\mathrm{1}\right)\mathrm{we}\:\mathrm{get}\:\mathrm{H}\left(\mathrm{0}\right)>\mathrm{0},\mathrm{H}\left(\mathrm{1}\right)>\mathrm{0} \\ $$$$\Rightarrow\mathrm{kH}\left(\mathrm{0}\right)<\mathrm{0},\mathrm{kH}\left(\mathrm{1}\right)<\mathrm{0}\Rightarrow\mathrm{H}\left(\mathrm{m}\right)>\mathrm{0} \\ $$$$\forall\mathrm{m}^{\mathrm{2}} \in\left[\mathrm{0},\mathrm{1}\right]\Leftrightarrow\mathrm{m}\in\left[−\mathrm{1},\mathrm{1}\right] \\ $$$$\left.\boldsymbol{\mathrm{F}}\left.\boldsymbol{\mathrm{rom}}\:\boldsymbol{\mathrm{i}}\right)\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{ii}}\right)\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{obtain}}\:\mathrm{1}<\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)<\mathrm{2}\left(\boldsymbol{\mathrm{q}}.\boldsymbol{\mathrm{e}}.\boldsymbol{\mathrm{d}}\right) \\ $$
Commented by 1549442205PVT last updated on 21/Aug/20
$$\mathrm{Thank}\:\mathrm{you},\mathrm{sir}.\mathrm{You}\:\mathrm{are}\:\mathrm{welcome} \\ $$
Commented by 1xx last updated on 24/Aug/20
![f(x)=(1/( (√(1+x))))+(1/( (√(1+a))))+((√(ax))/( (√(ax+8)))) x>0 , a>0 prove:1<f(x)<2 f^′ (x)=−((1/2))(1/((1+x)(√(1+x))))+(−(1/2))(1/((1+(8/(ax)))(√(1+(8/(ax))))))(8/a)(−(1/x^2 )) f^′ (x)=0⇒(x^2 −(8/a))[x^2 +(8/a)(3−(8/a))x+(8/a)]=0 ∵x>0 ∴x_1 =(√(8/a)) △=[8/a(3−8/a)]^2 −4(8/a)≥0⇒a≤2 f^′ (x)=0⇒ { ((f^′ (x_1 =(√(8/a)))=0 a≥2)),((f^′ (x_1 =(√(8/a)))=f^′ (x_(2,3) )=0 a<2)) :} case A: a≥2 f(x_1 =(√(8/a)))=(2/( (√(1+(√(8/a))))))+(1/( (√(1+a)))) lim_(x→0,∞) f(x)=1+(1/( (√(1+a)))) ∵a≥2 ∴(2/( (√(1+(√(8/a))))))>1 ∴ f_(max) =f(x_1 =(√(8/a))) f(x)>lim_(x→0,∞) f(x)=1+(1/( (√(1+a))))>1 f(x_1 =(√(8/a)))≷2 (2/( (√(1+(√(8/a))))))+(1/( (√(1+a))))≷2 let t=(√(1+(√(8/a)))) then a=(8/((t^2 −1)^2 )) (2/( (√(1+(√(8/a))))))+(1/( (√(1+a))))≷2 ⇔(((t^2 −1)^2 )/((t^2 −1)^2 +8))≷4∙(((t−1)^2 )/t^2 ) ⇔0≷3t^4 −2t^3 −9t^2 +36 ⇔0≷2(t−1)t^3 +(t^2 −6)^2 +3t^2 ∵t>1 ∴(2/( (√(1+(√(8/a))))))+(1/( (√(1+a))))<2 ∴f(x)≤f_(max) =f(x_1 =(√(8/a)))<2 ∵f(x)>lim_(x→0,∞) f(x)=1+(1/( (√(1+a))))>1 ∴ 1<f(x)<2 case B: 0<a<2 f^′ (x_(2,3) )=0 ⇒ x_(2,3) ^2 +(8/a)(3−(8/a))x_(2,3) +(8/a)=0 ⇒x_2 x_3 =(8/a) ∵x_1 =(√(8/a)) ∴x_2 <x_1 <x_3 x_(2,3) ^2 +(8/a)(3−(8/a))x_(2,3) +(8/a)=0 let p=x_(2,3) (ap)^2 +8(3a−8)p+8a=0 ⇒ (ap+8)(ap+a)=(8+a)(ap)+8(8−3a)p ⇒ a(ap+8)(p+1)=(a^2 −16a+64)p ⇒ (1/(1+p))∙((ap)/(ap+8))=(a^2 /((8−a)^2 )) ⇒ (1/( (√(1+x_(2,3) ))))∙((√(ax_(2,3) ))/( (√(ax_(2,3) +8))))=(a/(8−a)) due to 0<a<2 let m=(1/( (√(1+x_(2,3) )))) and n=((√(ax_(2,3) ))/( (√(ax_(2,3) +8)))) then { ((((1/m^2 )−1)((1/n^2 )−1)=(8/a))),((mn=(a/(8−a)))) :} ⇒ (m+n)^2 =1+mn=(8/(8−a)) ⇒ m+n=(√(8/(8−a))) f(x_(2,3) )≷f(x_1 ) ⇔( m+n)≷(2/( (√(1+(√(8/a)))))) ⇔ (√(8/(8−a)))≷(2/( (√(1+(√(8/a)))))) ⇔ ((√8)/( (√(((√8)−(√a))((√8)+(√a))))))≷((2(√(√a)))/( (√(((√8)+(√a)))))) ⇔ (√8)≷(√(4(√a)∙((√8)−(√a)))) ⇔ ((√2))^2 ≷2(√2)(√a)−((√a))^2 ⇔ ((√a)−(√2))^2 ≷0 ∵((√a)−(√2))^2 >0 ∴ f(x_(2,3) )>f(x_1 ) f_(max) =max{f(x_2 ),f(x_3 )}≷2 ⇔( m+n+(1/( (√(1+a)))))≷2 ⇔ (1/2)((√(8/(8−a)))+(1/( (√(1+a)))))≷1 ∵ (1/2)((√(8/(8−a)))+(1/( (√(1+a)))))≤(√((1/2)((8/(8−a)))+(1/(1+a)))) ∴ f_(max) =max{f(x_2 ),f(x_3 )}≷2 ⇔ (√((1/2)((8/(8−a)))+(1/(1+a))))≷1 ⇔ 0≷a(7−2a) ∵ 0<a<2 ∴ 0<a(7−2a) ∴ f_(max) =max{f(x_2 ),f(x_3 )}<2 if f(x_1 )>lim_(x→0,∞) f(x)=1+(1/( (√(1+a))))>1 then 1<f(x)<2 else f_(min) =f(x_1 ) f_(min) =f(x_1 )≷1 ⇔ (2/( (√(1+(√(8/a))))))≷(1−(1/( (√(1+a))))) make Rt△ ((1/( (√(1+a)))))^2 +(((√a)/( (√(1+a)))))^2 =1^2 ∴ ((√a)/( (√(1+a))))>1−(1/( (√(1+a)))) think of (2/( (√(1+(√(8/a))))))≷((√a)/( (√(1+a)))) ⇔ 3a−(√8)(√a)+4≷0 ⇔ 2a+((√a))^2 −2(√2)(√a)+((√2))^2 +2≷0 ⇔ 2a+((√a)−(√2))^2 +2≷0 ∵ a>0 ∴ 2a+((√a)−(√2))^2 +2>0 therefore (2/( (√(1+(√(8/a))))))>((√a)/( (√(1+a))))>1−(1/( (√(1+a)))) f_(min) =f(x_1 )>1 so in case B, 1<f(x)<2 Q.E.D](https://www.tinkutara.com/question/Q109104.png)
$$ \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}}+\frac{\sqrt{{ax}}}{\:\sqrt{{ax}+\mathrm{8}}} \\ $$$${x}>\mathrm{0}\:,\:{a}>\mathrm{0} \\ $$$${prove}:\mathrm{1}<{f}\left({x}\right)<\mathrm{2} \\ $$$${f}^{'} \left({x}\right)=−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\frac{\mathrm{1}}{\left(\mathrm{1}+{x}\right)\sqrt{\mathrm{1}+{x}}}+\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\frac{\mathrm{1}}{\left(\mathrm{1}+\frac{\mathrm{8}}{{ax}}\right)\sqrt{\mathrm{1}+\frac{\mathrm{8}}{{ax}}}}\left(\mathrm{8}/{a}\right)\left(−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right) \\ $$$${f}^{'} \left({x}\right)=\mathrm{0}\Rightarrow\left({x}^{\mathrm{2}} −\frac{\mathrm{8}}{{a}}\right)\left[{x}^{\mathrm{2}} +\frac{\mathrm{8}}{{a}}\left(\mathrm{3}−\frac{\mathrm{8}}{{a}}\right){x}+\frac{\mathrm{8}}{{a}}\right]=\mathrm{0} \\ $$$$\because{x}>\mathrm{0} \\ $$$$\therefore{x}_{\mathrm{1}} =\sqrt{\mathrm{8}/{a}} \\ $$$$\bigtriangleup=\left[\mathrm{8}/{a}\left(\mathrm{3}−\mathrm{8}/{a}\right)\right]^{\mathrm{2}} −\mathrm{4}\left(\mathrm{8}/{a}\right)\geqslant\mathrm{0}\Rightarrow{a}\leqslant\mathrm{2} \\ $$$${f}^{'} \left({x}\right)=\mathrm{0}\Rightarrow\begin{cases}{{f}^{'} \left({x}_{\mathrm{1}} =\sqrt{\mathrm{8}/{a}}\right)=\mathrm{0}\:\:{a}\geqslant\mathrm{2}}\\{{f}^{'} \left({x}_{\mathrm{1}} =\sqrt{\mathrm{8}/{a}}\right)={f}^{'} \left({x}_{\mathrm{2},\mathrm{3}} \right)=\mathrm{0}\:\:{a}<\mathrm{2}}\end{cases} \\ $$$$ \\ $$$${case}\:{A}:\:{a}\geqslant\mathrm{2} \\ $$$${f}\left({x}_{\mathrm{1}} =\sqrt{\mathrm{8}/{a}}\right)=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}+\sqrt{\frac{\mathrm{8}}{{a}}}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}} \\ $$$$\underset{{x}\rightarrow\mathrm{0},\infty} {\mathrm{lim}}{f}\left({x}\right)=\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}} \\ $$$$\because{a}\geqslant\mathrm{2} \\ $$$$\therefore\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}+\sqrt{\frac{\mathrm{8}}{{a}}}}}>\mathrm{1} \\ $$$$\therefore\:{f}_{{max}} ={f}\left({x}_{\mathrm{1}} =\sqrt{\mathrm{8}/{a}}\right) \\ $$$${f}\left({x}\right)>\underset{{x}\rightarrow\mathrm{0},\infty} {\mathrm{lim}}{f}\left({x}\right)=\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}}>\mathrm{1} \\ $$$${f}\left({x}_{\mathrm{1}} =\sqrt{\mathrm{8}/{a}}\right)\gtrless\mathrm{2} \\ $$$$\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}+\sqrt{\frac{\mathrm{8}}{{a}}}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}}\gtrless\mathrm{2} \\ $$$${let}\:{t}=\sqrt{\mathrm{1}+\sqrt{\frac{\mathrm{8}}{{a}}}} \\ $$$${then}\:{a}=\frac{\mathrm{8}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}+\sqrt{\frac{\mathrm{8}}{{a}}}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}}\gtrless\mathrm{2}\:\Leftrightarrow\frac{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\mathrm{8}}\gtrless\mathrm{4}\centerdot\frac{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }{{t}^{\mathrm{2}} } \\ $$$$\Leftrightarrow\mathrm{0}\gtrless\mathrm{3}{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{3}} −\mathrm{9}{t}^{\mathrm{2}} +\mathrm{36} \\ $$$$\Leftrightarrow\mathrm{0}\gtrless\mathrm{2}\left({t}−\mathrm{1}\right){t}^{\mathrm{3}} +\left({t}^{\mathrm{2}} −\mathrm{6}\right)^{\mathrm{2}} +\mathrm{3}{t}^{\mathrm{2}} \\ $$$$\because{t}>\mathrm{1} \\ $$$$\therefore\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}+\sqrt{\frac{\mathrm{8}}{{a}}}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}}<\mathrm{2}\: \\ $$$$\therefore{f}\left({x}\right)\leqslant{f}_{{max}} ={f}\left({x}_{\mathrm{1}} =\sqrt{\mathrm{8}/{a}}\right)<\mathrm{2} \\ $$$$\because{f}\left({x}\right)>\underset{{x}\rightarrow\mathrm{0},\infty} {\mathrm{lim}}{f}\left({x}\right)=\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}}>\mathrm{1} \\ $$$$\therefore\:\mathrm{1}<{f}\left({x}\right)<\mathrm{2} \\ $$$$ \\ $$$${case}\:{B}:\:\mathrm{0}<{a}<\mathrm{2} \\ $$$${f}^{'} \left({x}_{\mathrm{2},\mathrm{3}} \right)=\mathrm{0}\:\:\Rightarrow\:{x}_{\mathrm{2},\mathrm{3}} ^{\mathrm{2}} +\frac{\mathrm{8}}{{a}}\left(\mathrm{3}−\frac{\mathrm{8}}{{a}}\right){x}_{\mathrm{2},\mathrm{3}} +\frac{\mathrm{8}}{{a}}=\mathrm{0} \\ $$$$\Rightarrow{x}_{\mathrm{2}} {x}_{\mathrm{3}} =\frac{\mathrm{8}}{{a}} \\ $$$$\because{x}_{\mathrm{1}} =\sqrt{\frac{\mathrm{8}}{{a}}} \\ $$$$\therefore{x}_{\mathrm{2}} <{x}_{\mathrm{1}} <{x}_{\mathrm{3}} \\ $$$${x}_{\mathrm{2},\mathrm{3}} ^{\mathrm{2}} +\frac{\mathrm{8}}{{a}}\left(\mathrm{3}−\frac{\mathrm{8}}{{a}}\right){x}_{\mathrm{2},\mathrm{3}} +\frac{\mathrm{8}}{{a}}=\mathrm{0} \\ $$$${let}\:{p}={x}_{\mathrm{2},\mathrm{3}} \\ $$$$\left({ap}\right)^{\mathrm{2}} +\mathrm{8}\left(\mathrm{3}{a}−\mathrm{8}\right){p}+\mathrm{8}{a}=\mathrm{0}\:\Rightarrow \\ $$$$\left({ap}+\mathrm{8}\right)\left({ap}+{a}\right)=\left(\mathrm{8}+{a}\right)\left({ap}\right)+\mathrm{8}\left(\mathrm{8}−\mathrm{3}{a}\right){p}\:\Rightarrow \\ $$$${a}\left({ap}+\mathrm{8}\right)\left({p}+\mathrm{1}\right)=\left({a}^{\mathrm{2}} −\mathrm{16}{a}+\mathrm{64}\right){p}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{p}}\centerdot\frac{{ap}}{{ap}+\mathrm{8}}=\frac{{a}^{\mathrm{2}} }{\left(\mathrm{8}−{a}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}_{\mathrm{2},\mathrm{3}} }}\centerdot\frac{\sqrt{{ax}_{\mathrm{2},\mathrm{3}} }}{\:\sqrt{{ax}_{\mathrm{2},\mathrm{3}} +\mathrm{8}}}=\frac{{a}}{\mathrm{8}−{a}}\:\:{due}\:{to}\:\mathrm{0}<{a}<\mathrm{2} \\ $$$${let}\:{m}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}_{\mathrm{2},\mathrm{3}} }} \\ $$$${and}\:{n}=\frac{\sqrt{{ax}_{\mathrm{2},\mathrm{3}} }}{\:\sqrt{{ax}_{\mathrm{2},\mathrm{3}} +\mathrm{8}}} \\ $$$${then}\:\begin{cases}{\left(\frac{\mathrm{1}}{{m}^{\mathrm{2}} }−\mathrm{1}\right)\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\mathrm{1}\right)=\frac{\mathrm{8}}{{a}}}\\{{mn}=\frac{{a}}{\mathrm{8}−{a}}}\end{cases}\:\Rightarrow \\ $$$$\left({m}+{n}\right)^{\mathrm{2}} =\mathrm{1}+{mn}=\frac{\mathrm{8}}{\mathrm{8}−{a}}\:\Rightarrow \\ $$$${m}+{n}=\sqrt{\frac{\mathrm{8}}{\mathrm{8}−{a}}} \\ $$$${f}\left({x}_{\mathrm{2},\mathrm{3}} \right)\gtrless{f}\left({x}_{\mathrm{1}} \right)\:\Leftrightarrow\left(\:{m}+{n}\right)\gtrless\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}+\sqrt{\frac{\mathrm{8}}{{a}}}}} \\ $$$$\Leftrightarrow\:\sqrt{\frac{\mathrm{8}}{\mathrm{8}−{a}}}\gtrless\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}+\sqrt{\frac{\mathrm{8}}{{a}}}}} \\ $$$$\Leftrightarrow\:\frac{\sqrt{\mathrm{8}}}{\:\sqrt{\left(\sqrt{\mathrm{8}}−\sqrt{{a}}\right)\left(\sqrt{\mathrm{8}}+\sqrt{{a}}\right)}}\gtrless\frac{\mathrm{2}\sqrt{\sqrt{{a}}}}{\:\sqrt{\left(\sqrt{\mathrm{8}}+\sqrt{{a}}\right)}} \\ $$$$\Leftrightarrow\:\sqrt{\mathrm{8}}\gtrless\sqrt{\mathrm{4}\sqrt{{a}}\centerdot\left(\sqrt{\mathrm{8}}−\sqrt{{a}}\right)} \\ $$$$\Leftrightarrow\:\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \gtrless\mathrm{2}\sqrt{\mathrm{2}}\sqrt{{a}}−\left(\sqrt{{a}}\right)^{\mathrm{2}} \\ $$$$\Leftrightarrow\:\left(\sqrt{{a}}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \gtrless\mathrm{0} \\ $$$$\because\left(\sqrt{{a}}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}} >\mathrm{0} \\ $$$$\therefore\:{f}\left({x}_{\mathrm{2},\mathrm{3}} \right)>{f}\left({x}_{\mathrm{1}} \right) \\ $$$${f}_{{max}} ={max}\left\{{f}\left({x}_{\mathrm{2}} \right),{f}\left({x}_{\mathrm{3}} \right)\right\}\gtrless\mathrm{2} \\ $$$$\Leftrightarrow\left(\:{m}+{n}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}}\right)\gtrless\mathrm{2} \\ $$$$\Leftrightarrow\:\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\frac{\mathrm{8}}{\mathrm{8}−{a}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}}\right)\gtrless\mathrm{1} \\ $$$$\because\:\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\frac{\mathrm{8}}{\mathrm{8}−{a}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}}\right)\leqslant\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{8}}{\mathrm{8}−{a}}\right)+\frac{\mathrm{1}}{\mathrm{1}+{a}}} \\ $$$$\therefore\:{f}_{{max}} ={max}\left\{{f}\left({x}_{\mathrm{2}} \right),{f}\left({x}_{\mathrm{3}} \right)\right\}\gtrless\mathrm{2} \\ $$$$\Leftrightarrow\:\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{8}}{\mathrm{8}−{a}}\right)+\frac{\mathrm{1}}{\mathrm{1}+{a}}}\gtrless\mathrm{1} \\ $$$$\Leftrightarrow\:\mathrm{0}\gtrless{a}\left(\mathrm{7}−\mathrm{2}{a}\right) \\ $$$$\because\:\mathrm{0}<{a}<\mathrm{2} \\ $$$$\therefore\:\mathrm{0}<{a}\left(\mathrm{7}−\mathrm{2}{a}\right) \\ $$$$\therefore\:{f}_{{max}} ={max}\left\{{f}\left({x}_{\mathrm{2}} \right),{f}\left({x}_{\mathrm{3}} \right)\right\}<\mathrm{2} \\ $$$${if}\:{f}\left({x}_{\mathrm{1}} \right)>\underset{{x}\rightarrow\mathrm{0},\infty} {\mathrm{lim}}{f}\left({x}\right)=\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}}>\mathrm{1} \\ $$$$\:\:\:\:\:\:{then}\:\mathrm{1}<{f}\left({x}\right)<\mathrm{2} \\ $$$${else}\:{f}_{{min}} ={f}\left({x}_{\mathrm{1}} \right) \\ $$$${f}_{{min}} ={f}\left({x}_{\mathrm{1}} \right)\gtrless\mathrm{1} \\ $$$$\Leftrightarrow\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}+\sqrt{\frac{\mathrm{8}}{{a}}}}}\gtrless\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}}\right) \\ $$$${make}\:{Rt}\bigtriangleup\:\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{1}+{a}}}\right)^{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} \\ $$$$\therefore\:\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{1}+{a}}}>\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}} \\ $$$${think}\:{of}\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}+\sqrt{\frac{\mathrm{8}}{{a}}}}}\gtrless\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{1}+{a}}} \\ $$$$\Leftrightarrow\:\mathrm{3}{a}−\sqrt{\mathrm{8}}\sqrt{{a}}+\mathrm{4}\gtrless\mathrm{0} \\ $$$$\Leftrightarrow\:\mathrm{2}{a}+\left(\sqrt{{a}}\right)^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}\sqrt{{a}}+\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}\gtrless\mathrm{0} \\ $$$$\Leftrightarrow\:\mathrm{2}{a}+\left(\sqrt{{a}}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}\gtrless\mathrm{0} \\ $$$$\because\:{a}>\mathrm{0} \\ $$$$\therefore\:\mathrm{2}{a}+\left(\sqrt{{a}}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}>\mathrm{0} \\ $$$${therefore}\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}+\sqrt{\frac{\mathrm{8}}{{a}}}}}>\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{1}+{a}}}>\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}} \\ $$$${f}_{{min}} ={f}\left({x}_{\mathrm{1}} \right)>\mathrm{1} \\ $$$${so}\:{in}\:{case}\:{B},\:\mathrm{1}<{f}\left({x}\right)<\mathrm{2} \\ $$$$ \\ $$$${Q}.{E}.{D} \\ $$$$ \\ $$
Commented by 1xx last updated on 21/Aug/20
$${Thank}\:{to}\:{have}\:{chance}\:{to}\:{learn}\:{from}\:{you}. \\ $$$${I}\:{have}\:{finished}\:{a}\:{proof}\:{that}\:{is}\:{a}\:{little} \\ $$$${bit}\:{complex}.\:{I}\:{think}\:{it}\:{can}\:{be}\:{improved} \\ $$$${by}\:{merging}\:{your}\:{idea}. \\ $$
Commented by 1xx last updated on 21/Aug/20
$${we}\:{need}\:{to}\:{confirm}\:: \\ $$$$\left(\mathrm{1}+{m}\right)\left(−{m}^{\mathrm{3}} +{m}^{\mathrm{2}} +\mathrm{14}{m}+\mathrm{8}\right)>\mathrm{0} \\ $$$${in}\:{case}\:{of}\:−\mathrm{1}<{m}<−\mathrm{2}/\mathrm{3}. \\ $$$${when}\:{m}=−.\mathrm{99},\:{can}\:{find} \\ $$$$\:\left(\mathrm{1}+{m}\right)\left(−{m}^{\mathrm{3}} +{m}^{\mathrm{2}} +\mathrm{14}{m}+\mathrm{8}\right)<\mathrm{0} \\ $$$$ \\ $$$$ \\ $$
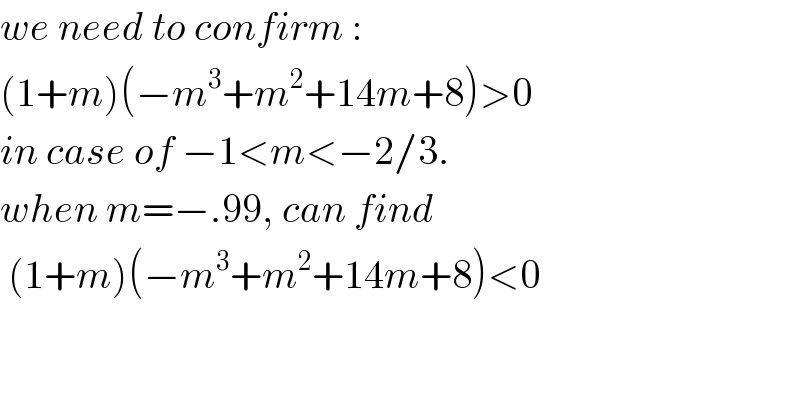
Answered by 1xx last updated on 20/Aug/20
$${in}\:{case}\:{ii}\:\left({prove}\:{f}\left({x}\right)<\mathrm{2}\right) \\ $$$$\boldsymbol{\mathrm{due}}\:\boldsymbol{\mathrm{to}}\:\mathrm{0}<\boldsymbol{\mathrm{m}}\leqslant\mathrm{1}\:??? \\ $$$${pls}\:{note}:\:{m}\:{may}\:{be}\:<\:{zero}. \\ $$$$ \\ $$$${in}\:{case}\:{i}\left({prove}\:{f}\left({x}\right)>\mathrm{1}\right),{we}\:{can}\:{assume}\:\mathrm{0}<{m}<\mathrm{1} \\ $$$${but}\:{it}\:{is}\:{different}\:{in}\:{case}\:{ii}\left({prove}\:{f}\left({x}\right)<\mathrm{2}\right) \\ $$
Commented by 1549442205PVT last updated on 20/Aug/20
$$\mathrm{Above}\:\mathrm{we}\:\mathrm{limit}\:\mathrm{only}\:\mathrm{consider}\:\mathrm{the}\: \\ $$$$\mathrm{z}+\mathrm{y}<\mathrm{1}\Rightarrow\mathrm{m}=\mathrm{1}−\left(\mathrm{z}+\mathrm{y}\right)>\mathrm{0} \\ $$$$\left.\mathrm{For}\:\mathrm{ii}\right)\:\mathrm{Thank}\:\mathrm{you},\mathrm{i}\:\mathrm{missed}\:\mathrm{the}\:\mathrm{case} \\ $$$$.\mathrm{z}+\mathrm{y}>\mathrm{1}.\mathrm{Please}, \\ $$$$\mathrm{waiting}\:\mathrm{for}\:\:\mathrm{i}\:\mathrm{look}\:\mathrm{at}\:\mathrm{again}.\mathrm{Corrected} \\ $$
Commented by 1xx last updated on 20/Aug/20
$$ \\ $$$$ \\ $$$${for}\:{the}\:{same}\:{reason},\:{please}\:{consider} \\ $$$${zy}<\mathrm{1}/\mathrm{4}\:???\:{in}\:{case}\:{ii}\left({prove}\:{f}\left({x}\right)<\mathrm{2}\right) \\ $$
Commented by 1xx last updated on 20/Aug/20
$${in}\:{case}\:{of}\:\bigtriangleup_{{H}} <\mathrm{0},\:{we}\:{need}\:{to}\:{prove}\:\mathrm{9}{m}^{\mathrm{2}} +\mathrm{18}{m}+\mathrm{8}>\mathrm{0}\: \\ $$$$\mathrm{9}{m}^{\mathrm{2}} +\mathrm{18}{m}+\mathrm{8}=\mathrm{9}\left({m}^{\mathrm{2}} +\mathrm{2}{m}+\mathrm{1}\right)−\mathrm{1} \\ $$$$=\mathrm{9}\left({m}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1} \\ $$$$\Leftrightarrow\mid{m}+\mathrm{1}\mid>\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${but}\:\mid{m}\mid\leqslant\mathrm{1},\:{only}! \\ $$$${Q}.{E}.{D}.\:{is}\:{not}\:{achieved}. \\ $$$${Very}\:{happy}\:{to}\:{discuss}\:{with}\:{you}. \\ $$$${ps}:\:\mathrm{0}<{zy}\leqslant\left(\frac{{z}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}\right)\leqslant\mathrm{1}\:{or}\:\mathrm{0}<{zy}\leqslant\left(\frac{{z}+{y}}{\mathrm{2}}\right)^{\mathrm{2}} \leqslant\mathrm{1}\: \\ $$
Commented by 1xx last updated on 20/Aug/20
$$ \\ $$$$\left.{f}\left.{or}\:{i}\right)\right),\:\bigtriangleup_{{Q}} >\mathrm{0}\:{need}\:{a}\:{proof}\:{in}\:{case}\:{of}\:\mathrm{0}<{zy}<\mathrm{1}/\mathrm{4} \\ $$$${we}\:{should}\:{prove}\:\frac{{d}}{{dt}}\left(\bigtriangleup_{{Q}} \right)=\mathrm{0}\:{have}\:{no}\:{root}\:{in}\:\left(\mathrm{0},\mathrm{1}/\mathrm{4}\right) \\ $$$${or}\:{we}\:{have}\:{to}\:{consider}\:{min}\left(\bigtriangleup_{{Q}} \right)\wedge\mathrm{0} \\ $$$$ \\ $$
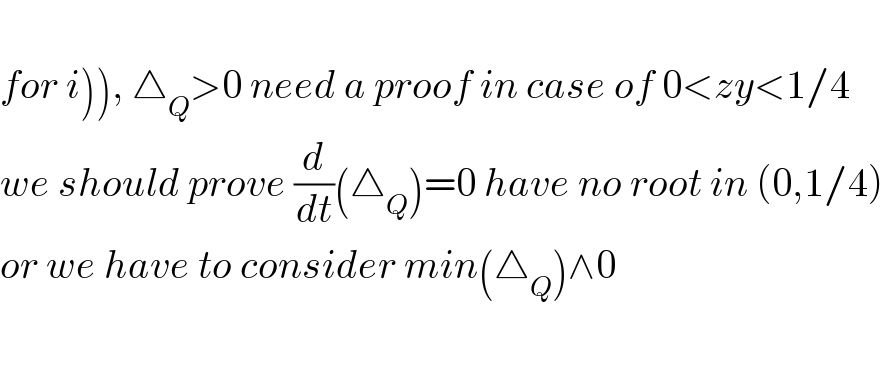
Commented by 1549442205PVT last updated on 21/Aug/20
$$\mathrm{Don}'\mathrm{t}\:\mathrm{need}\:\mathrm{to}\:\mathrm{consider}\:\Delta\:\mathrm{because} \\ $$$$\mathrm{kf}\left(\alpha\right)<\mathrm{0}\Leftrightarrow\Delta>\mathrm{0}\:\mathrm{and}\:\mathrm{x}_{\mathrm{1}} <\alpha<\mathrm{x}_{\mathrm{2}} \\ $$