Q58885-reposted-How-many-4-digit-numbers-abcd-exist-which-are-divisible-by-3-and-satisfy-a-b-c-d-

Question Number 59021 by mr W last updated on 03/May/19

[Q 58885 r e p o s t e d]

H o w m a n y 4 - d i g i t n u m b e r s a b c d e x i s t

w h i c h a r e d i v i s i b l e b y 3 a n d s a t i s f y

a ⩽ b ⩽ c ⩽ d ?

Commented by tanmay last updated on 03/May/19

i s t h e r e a n y c o - r e l a t i o n b e t w e e n t h i s p r o b l e m

a n d E u l e r e n u m e r a t i o n p a r t i t i o n \dots

Commented by mr W last updated on 03/May/19

{I t}^{'} s n o t a s e a s y a s I t h o u g h t . P l e a s e

g i v e a t r y .

Commented by Kunal12588 last updated on 03/May/19

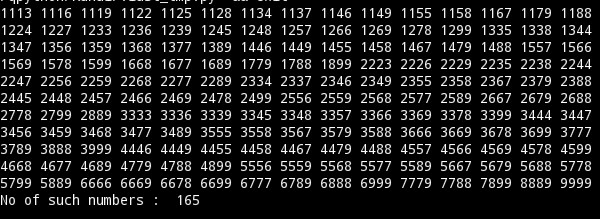
Commented by Kunal12588 last updated on 03/May/19

I think it may help someone who is trying to solve the problem.

Commented by mr W last updated on 03/May/19

t h a n k y o u s i r!

c a n y o u g i v e a f o r m u l a h o w t o c a l c u l a t e t h e

n u m b e r w i t h o u t k n o w i n g t h e n u m b e r s

t h e m s e l v e s ?

Commented by mr W last updated on 03/May/19

m y f o r m u l a (n o t e x a c t l y p r o v e d y e t) i s

\frac{C_{9 - 1}^{4 + 9 - 1}}{3} = \frac{C_{8}^{12}}{3} = \frac{495}{3} = 165

i n c a s e o f 5 - d i g i t n u m b e r s i t i s

\frac{C_{9 - 1}^{5 + 9 - 1}}{3} = \frac{C_{8}^{13}}{3} = \frac{1287}{3} = 429

i n c a s e o f 6 - d i g i t n u m b e r s i t i s

\frac{C_{9 - 1}^{6 + 9 - 1}}{3} = \frac{C_{8}^{14}}{3} = \frac{3003}{3} = 1001

c a n y o u c h e c k t h e m u s i n g y o u r m e t h o d ?

Commented by mr W last updated on 03/May/19

a j f o u r s i r, M J S s i r, t a n m a y s i r :

c a n y o u p l e a s e a l s o h a v e a l o o k a t t h i s

p r o b l e m ?

Commented by Kunal12588 last updated on 03/May/19

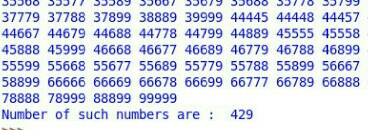
Commented by Kunal12588 last updated on 03/May/19

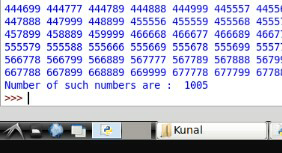
Commented by Kunal12588 last updated on 03/May/19

Sir MrW you are correct with 5-digit numbers There are 429 such numbers. but for 6-digit number they are total 1005.

Answered by Rasheed.Sindhi last updated on 03/May/19

I {d o n}^{'} t k n o w a n y f o r m u l a . I w a n t t o

t h i n k a b o u t^{'} {p r o c e s s}^{'} o f d e t e r m i n i n g

r e q u i r e d n u m b e r . A l t h o u g h I^{'} m n o t

s u r e o f m y p r o c e s s b e i n g u s e f u l a t

t h i s s t a g e .

I t h i n k u p t o t h r e e d i g i t s w e n e e d n o t

b e a n x i o u s a b o u t d i v i s i b i l i t y o f 3 .

{I t}^{'} s o n l y f i x a t i o n o f o n e d i g i t w h i c h

m a k e s t h e n u m b e r d i v i s i b l e b y 3 .

S o u p t o a b c w e s h o u l d c o n s i d e r o n l y o n e

c o n d i t i o n t h a t i s a ⩽ b ⩽ c .

T h e f o u r t h d i g i t (u n i t) d m a y b e f i x e d

i n s u c h a w a y t h a t i t m a k e s t h e n u m b e r

m u l t i p l e o f 3 a l o n g w i t h d ⩾ c .

P a r t i c u l a r i l y i f a_{0} b_{0} c_{0} i s a n y o f s u c h

p e r m u t a t i o n s a n d d i s u n i t d i g i t t h e n

f o r 3 m > a_{0} + b_{0} + c_{0} & 1 ⩽ 3 m - (a_{0} + b_{0} + c_{0}) ⩽ 9 :

d ⩾ c \land d = 3 m - (a_{0} + b_{0} + c_{0})

F o r e x a m p l e i f a b c = 112

A c c o r d i n g t o t h e c o n d i t i o n d ⩾ c, t h e

c a n d i d a t e s f o r d a r e 2, 3, 4, \dots, 9 b u t

o n l y 2, 5 & 8 a r e s u c h w h i c h m a k e

t h e n u m b e r d i v i s i b l e b y 3 . S o t h r e e

n u m b e r s (1122, 1125 & 1128) c a n b e

m a d e f r o m 112

T h e l i m i t a t i o n o f t h e p r o c e s s i s t h i s

t h a t w e h a v e t o c o m p o s e a l l t h e t h r e e

d i g i t n u m b e r s a b c w i t h c o n d i t i o n

a ⩽ b ⩽ c

S o t h i s i s n o t a g o o d m e t h o d t o d e t e r m i n e

n u m b e r o f t h e r e q u i r e d n u m b e r s .

H o w e v e r i t m a y b e u s e d t o c o n s t r u c t

n u m b e r s u n d e r t h e g i v e n c o n d i t i o n s

Answered by Rasheed.Sindhi last updated on 04/May/19

C a s e - 1 : W h e n a + b + c + d = 3

N o p o s s i b i l i t y b e c a u s e 1111 i s t h e

s m a l l e s t n u m b e r u n d e r c o n d i t i o n

a ⩽ b ⩽ c ⩽ d

C a s e - 2 : W h e n a + b + c + d = 6

C a s e - 3 : W h e n a + b + c + d = 9

C a s e - 12 : W h e n a + b + c + d = 36

\dots \dots . .

\dots \dots .

Commented by mr W last updated on 03/May/19

t h a n k y o u R a s h e e d s i r f o r s h a r i n g

y o u r t h o u g h t s!

Commented by mr W last updated on 03/May/19

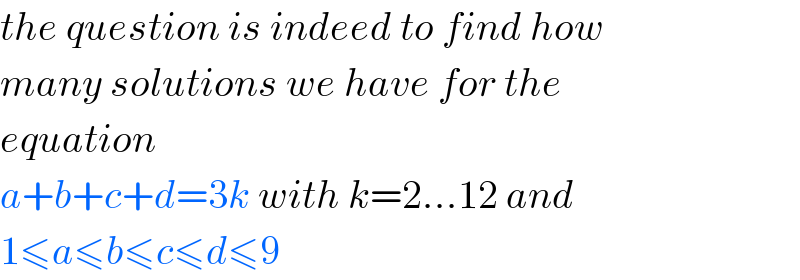
t h e q u e s t i o n i s i n d e e d t o f i n d h o w

m a n y s o l u t i o n s w e h a v e f o r t h e

e q u a t i o n

a + b + c + d = 3 k w i t h k = 2 \dots 12 a n d

1 ⩽ a ⩽ b ⩽ c ⩽ d ⩽ 9

Commented by Rasheed.Sindhi last updated on 03/May/19

T h e p r o b l e m g o e s t o “ n u m b e r o f

{p a r t i t i o n s}^{″} u n d e r s o m e c o n d i t i o n s .

F o r e x a m p l e : I n h o w m a n y w a y s

6 c a n b e p a r t i t i o n e d i n f o u r p a r t s

a, b, c, d s u c h t h a t

1 ⩽ a, b, c, d ⩽ 9 & a ⩽ b ⩽ c ⩽ d

Commented by Rasheed.Sindhi last updated on 04/May/19

S i r I w a n t t o d o t h e s a m e . I t h o u g h t

t h a t i f w e b e a b l e t o d e t e r m i n e t h e

n u m b e r o f p a r t i t i o n s o f a n i n t e g e r n

(i n t h i s c a s e n = 6, 9, \dots 36) i n k p a r t s

(i n o u r c a s e k = 4) w e c a n s o l v e o u r

p r o b l e m .