Question Number 100042 by bobhans last updated on 24/Jun/20
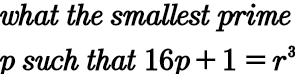
Answered by Rasheed.Sindhi last updated on 25/Jun/20

$$\:\:\:\mathrm{16}{p}={r}^{\mathrm{3}} −\mathrm{1} \\ $$$$\:\:\:\:\mathrm{16}{p}=\left({r}−\mathrm{1}\right)\left({r}^{\mathrm{2}} +{r}+\mathrm{1}\right) \\ $$$$\:\:\:\:{r}−\mathrm{1}=\mathrm{1},\mathrm{2},\mathrm{4},\mathrm{8},\mathrm{16},{p} \\ $$$$\:{r}=\mathrm{2},\mathrm{3},\mathrm{5},\mathrm{9},\mathrm{17},{p}+\mathrm{1}\:\left(\mathrm{possible}\:\mathrm{values}\right)\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:{p}=\frac{\left({r}−\mathrm{1}\right)\left({r}^{\mathrm{2}} +{r}+\mathrm{1}\right)}{\mathrm{16}} \\ $$$$\:^{\bullet} {r}=\mathrm{2}\Rightarrow{p}\:=\frac{\mathrm{7}}{\mathrm{16}}\notin\mathbb{P} \\ $$$$\:^{\bullet} {r}=\mathrm{3}\Rightarrow{p}=\frac{\mathrm{26}}{\mathrm{16}}\notin\mathbb{P} \\ $$$$\:^{\bullet} {r}=\mathrm{5}\Rightarrow{p}=\frac{\mathrm{4}×\mathrm{31}}{\mathrm{16}}\notin\mathbb{P} \\ $$$$\:^{\bullet} {r}=\mathrm{9}\Rightarrow{p}=\frac{\mathrm{8}×\mathrm{91}}{\mathrm{16}}\notin\mathbb{P} \\ $$$$\:^{\bullet} {r}=\mathrm{17}\Rightarrow{p}=\frac{\mathrm{16}×\mathrm{307}}{\mathrm{16}}=\mathrm{307}\in\mathbb{P} \\ $$$$\:^{\bullet} {r}−\mathrm{1}={p}\Rightarrow{r}^{\mathrm{2}} +{r}+\mathrm{1}=\mathrm{16} \\ $$$$\:\:\:\:\:\:\:{r}^{\mathrm{2}} +{r}−\mathrm{15}=\mathrm{0} \\ $$$$\:\:\:\:\:\Rightarrow{r}\notin\mathbb{N}\Rightarrow{r}−\mathrm{1}\notin\mathbb{P} \\ $$$$\:\:\:\:{p}=\mathrm{307}\:\left({unique}\:{solution}\right) \\ $$
Commented by bobhans last updated on 25/Jun/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by 1549442205 last updated on 27/Jun/20
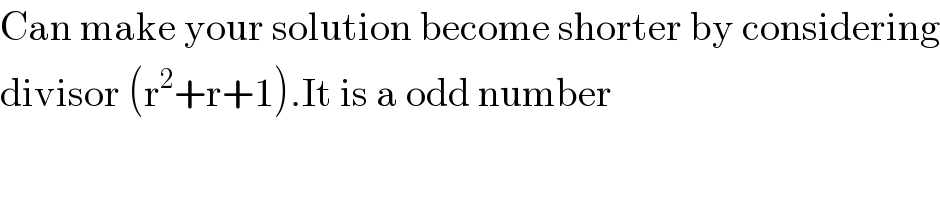
$$\mathrm{Can}\:\mathrm{make}\:\mathrm{your}\:\mathrm{solution}\:\mathrm{become}\:\mathrm{shorter}\:\mathrm{by}\:\mathrm{considering} \\ $$$$\mathrm{divisor}\:\left(\mathrm{r}^{\mathrm{2}} +\mathrm{r}+\mathrm{1}\right).\mathrm{It}\:\mathrm{is}\:\mathrm{a}\:\mathrm{odd}\:\mathrm{number} \\ $$
Commented by Rasheed.Sindhi last updated on 28/Jun/20
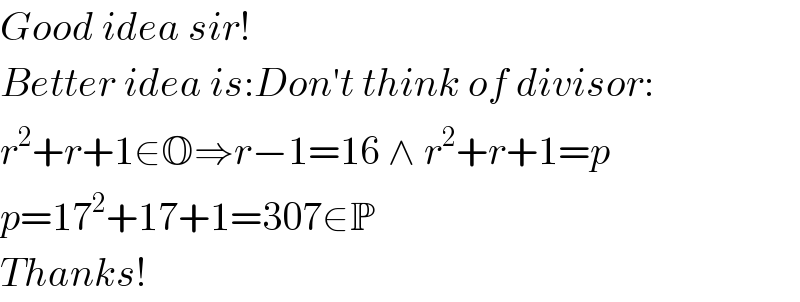
$${Good}\:{idea}\:{sir}! \\ $$$${Better}\:{idea}\:{is}:{Don}'{t}\:{think}\:{of}\:{divisor}: \\ $$$${r}^{\mathrm{2}} +{r}+\mathrm{1}\in\mathbb{O}\Rightarrow{r}−\mathrm{1}=\mathrm{16}\:\wedge\:{r}^{\mathrm{2}} +{r}+\mathrm{1}={p} \\ $$$${p}=\mathrm{17}^{\mathrm{2}} +\mathrm{17}+\mathrm{1}=\mathrm{307}\in\mathbb{P} \\ $$$${Thanks}! \\ $$
