Question Number 100065 by kungmikami last updated on 24/Jun/20

Answered by abdomathmax last updated on 24/Jun/20
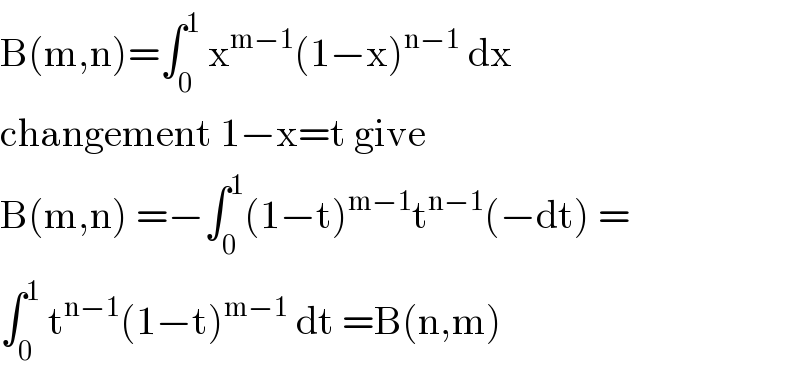
$$\mathrm{B}\left(\mathrm{m},\mathrm{n}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{m}−\mathrm{1}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{n}−\mathrm{1}} \:\mathrm{dx} \\ $$$$\mathrm{changement}\:\mathrm{1}−\mathrm{x}=\mathrm{t}\:\mathrm{give}\: \\ $$$$\mathrm{B}\left(\mathrm{m},\mathrm{n}\right)\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{m}−\mathrm{1}} \mathrm{t}^{\mathrm{n}−\mathrm{1}} \left(−\mathrm{dt}\right)\:= \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{t}^{\mathrm{n}−\mathrm{1}} \left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{m}−\mathrm{1}} \:\mathrm{dt}\:=\mathrm{B}\left(\mathrm{n},\mathrm{m}\right) \\ $$
Answered by abdomathmax last updated on 24/Jun/20
![I =∫_0 ^1 ∫_0 ^x^2 e^(y/x) dy dx ⇒I =∫_0 ^1 A(x)dx A(x) =∫_0 ^x^2 e^(y/x) dy =[xe^(y/x) ]_(y=0) ^x^2 =xe^x ⇒ I = ∫_0 ^1 xe^x dx =[xe^x ]_0 ^1 −∫_0 ^1 e^x dx =e−[e^x ]_0 ^1 =e−(e−1) =1](https://www.tinkutara.com/question/Q100071.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\int_{\mathrm{0}} ^{\mathrm{x}^{\mathrm{2}} } \:\mathrm{e}^{\frac{\mathrm{y}}{\mathrm{x}}} \mathrm{dy}\:\mathrm{dx}\:\Rightarrow\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{A}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{A}\left(\mathrm{x}\right)\:=\int_{\mathrm{0}} ^{\mathrm{x}^{\mathrm{2}} } \mathrm{e}^{\frac{\mathrm{y}}{\mathrm{x}}} \:\mathrm{dy}\:=\left[\mathrm{xe}^{\frac{\mathrm{y}}{\mathrm{x}}} \right]_{\mathrm{y}=\mathrm{0}} ^{\mathrm{x}^{\mathrm{2}} } \:=\mathrm{xe}^{\mathrm{x}} \:\Rightarrow \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{xe}^{\mathrm{x}} \:\mathrm{dx}\:=\left[\mathrm{xe}^{\mathrm{x}} \right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{e}^{\mathrm{x}} \:\mathrm{dx} \\ $$$$=\mathrm{e}−\left[\mathrm{e}^{\mathrm{x}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:=\mathrm{e}−\left(\mathrm{e}−\mathrm{1}\right)\:=\mathrm{1} \\ $$
Commented by kungmikami last updated on 24/Jun/20
thanks man
Commented by mathmax by abdo last updated on 24/Jun/20
![sorry A(x) =[xe^(y/x) ]_(y=0) ^x^2 =xe^x −x ⇒ I =∫_0 ^1 xe^x dx−∫_0 ^1 xdx =1−(1/2) ⇒ I =(1/2)](https://www.tinkutara.com/question/Q100086.png)
$$\mathrm{sorry}\:\mathrm{A}\left(\mathrm{x}\right)\:=\left[\mathrm{xe}^{\frac{\mathrm{y}}{\mathrm{x}}} \right]_{\mathrm{y}=\mathrm{0}} ^{\mathrm{x}^{\mathrm{2}} } \:=\mathrm{xe}^{\mathrm{x}} −\mathrm{x}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{xe}^{\mathrm{x}} \mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{xdx}\:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by smridha last updated on 24/Jun/20
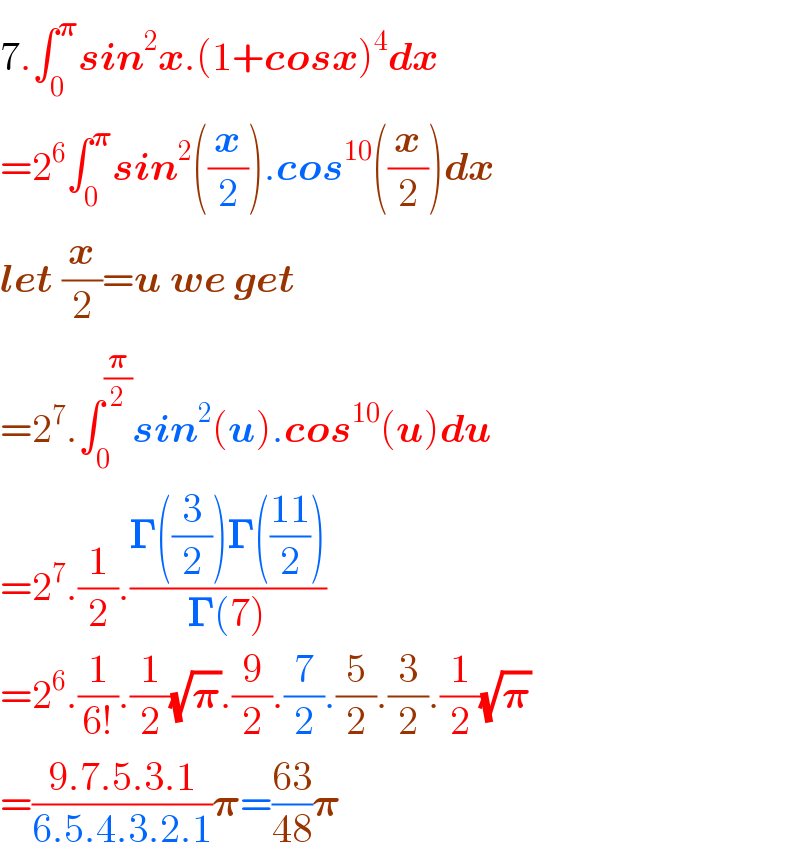
$$\mathrm{7}.\int_{\mathrm{0}} ^{\boldsymbol{\pi}} \boldsymbol{{sin}}^{\mathrm{2}} \boldsymbol{{x}}.\left(\mathrm{1}+\boldsymbol{{cosx}}\right)^{\mathrm{4}} \boldsymbol{{dx}} \\ $$$$=\mathrm{2}^{\mathrm{6}} \int_{\mathrm{0}} ^{\boldsymbol{\pi}} \boldsymbol{{sin}}^{\mathrm{2}} \left(\frac{\boldsymbol{{x}}}{\mathrm{2}}\right).\boldsymbol{{cos}}^{\mathrm{10}} \left(\frac{\boldsymbol{{x}}}{\mathrm{2}}\right)\boldsymbol{{dx}} \\ $$$$\boldsymbol{{let}}\:\frac{\boldsymbol{{x}}}{\mathrm{2}}=\boldsymbol{{u}}\:\boldsymbol{{we}}\:\boldsymbol{{get}} \\ $$$$=\mathrm{2}^{\mathrm{7}} .\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \boldsymbol{{sin}}^{\mathrm{2}} \left(\boldsymbol{{u}}\right).\boldsymbol{{cos}}^{\mathrm{10}} \left(\boldsymbol{{u}}\right)\boldsymbol{{du}} \\ $$$$=\mathrm{2}^{\mathrm{7}} .\frac{\mathrm{1}}{\mathrm{2}}.\frac{\boldsymbol{\Gamma}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\boldsymbol{\Gamma}\left(\frac{\mathrm{11}}{\mathrm{2}}\right)}{\boldsymbol{\Gamma}\left(\mathrm{7}\right)} \\ $$$$=\mathrm{2}^{\mathrm{6}} .\frac{\mathrm{1}}{\mathrm{6}!}.\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\boldsymbol{\pi}}.\frac{\mathrm{9}}{\mathrm{2}}.\frac{\mathrm{7}}{\mathrm{2}}.\frac{\mathrm{5}}{\mathrm{2}}.\frac{\mathrm{3}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\boldsymbol{\pi}} \\ $$$$=\frac{\mathrm{9}.\mathrm{7}.\mathrm{5}.\mathrm{3}.\mathrm{1}}{\mathrm{6}.\mathrm{5}.\mathrm{4}.\mathrm{3}.\mathrm{2}.\mathrm{1}}\boldsymbol{\pi}=\frac{\mathrm{63}}{\mathrm{48}}\boldsymbol{\pi} \\ $$
Answered by abdomathmax last updated on 24/Jun/20
![J =∫_0 ^1 ∫_x ^(2−x) (x/y)dy dx =∫_0 ^1 A(x)dx A(x) =∫_x ^(2−x) (x/y)dy =x[lny]_x ^(2−x) =x[ln(2−x)−lnx] ⇒J =∫_0 ^1 xln(2−x)dx−∫_0 ^1 xlnx dx but ∫_0 ^(1 ) xln(2−x)dx =[(x^2 /2)ln(2−x)]_0 ^1 +∫_0 ^1 (x^2 /2)(1/(2−x))dx =(1/2)∫_0 ^1 (x^2 /(2−x))dx =−(1/2)∫_0 ^1 ((x^2 −4+4)/(x−2))dx =−(1/2)∫_0 ^1 (x+2)−2∫_0 ^1 (dx/(x−2)) =−(1/2)[(x^2 /2)+2x]_0 ^1 −2[ln∣x−2∣]_0 ^1 =−(1/2)((5/2))−2(−ln2) =2ln2−(5/4) ∫_0 ^1 xlnxdx =[(x^2 /2)lnx]_0 ^1 −∫_0 ^1 (x^2 /2)(dx/x) =−(1/2)∫_0 ^1 xdx =−(1/2)[(x^2 /2)]_0 ^1 =−(1/4) ⇒ J =2ln2−(5/4)+(1/4) ⇒J =2ln2−1](https://www.tinkutara.com/question/Q100076.png)
$$\mathrm{J}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\int_{\mathrm{x}} ^{\mathrm{2}−\mathrm{x}} \:\frac{\mathrm{x}}{\mathrm{y}}\mathrm{dy}\:\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{A}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{A}\left(\mathrm{x}\right)\:=\int_{\mathrm{x}} ^{\mathrm{2}−\boldsymbol{\mathrm{x}}} \frac{\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{y}}}\boldsymbol{\mathrm{dy}}\:=\boldsymbol{\mathrm{x}}\left[\boldsymbol{\mathrm{lny}}\right]_{\boldsymbol{\mathrm{x}}} ^{\mathrm{2}−\boldsymbol{\mathrm{x}}} \:=\boldsymbol{\mathrm{x}}\left[\boldsymbol{\mathrm{ln}}\left(\mathrm{2}−\boldsymbol{\mathrm{x}}\right)−\boldsymbol{\mathrm{lnx}}\right] \\ $$$$\Rightarrow\mathrm{J}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{xln}\left(\mathrm{2}−\mathrm{x}\right)\mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{xlnx}\:\mathrm{dx}\:\mathrm{but} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}\:} \mathrm{xln}\left(\mathrm{2}−\mathrm{x}\right)\mathrm{dx}\:=\left[\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}−\mathrm{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\frac{\mathrm{1}}{\mathrm{2}−\mathrm{x}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}−\mathrm{x}}\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{4}+\mathrm{4}}{\mathrm{x}−\mathrm{2}}\boldsymbol{\mathrm{dx}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{x}+\mathrm{2}\right)−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{x}−\mathrm{2}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2}\boldsymbol{\mathrm{x}}\right]_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{2}\left[\boldsymbol{\mathrm{ln}}\mid\mathrm{x}−\mathrm{2}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{5}}{\mathrm{2}}\right)−\mathrm{2}\left(−\mathrm{ln2}\right)\:=\mathrm{2ln2}−\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{xlnxdx}\:=\left[\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\mathrm{lnx}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\frac{\mathrm{dx}}{\mathrm{x}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{xdx}\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{1}} \:=−\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow \\ $$$$\mathrm{J}\:=\mathrm{2ln2}−\frac{\mathrm{5}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\mathrm{J}\:=\mathrm{2ln2}−\mathrm{1} \\ $$$$ \\ $$
Answered by abdomathmax last updated on 24/Jun/20
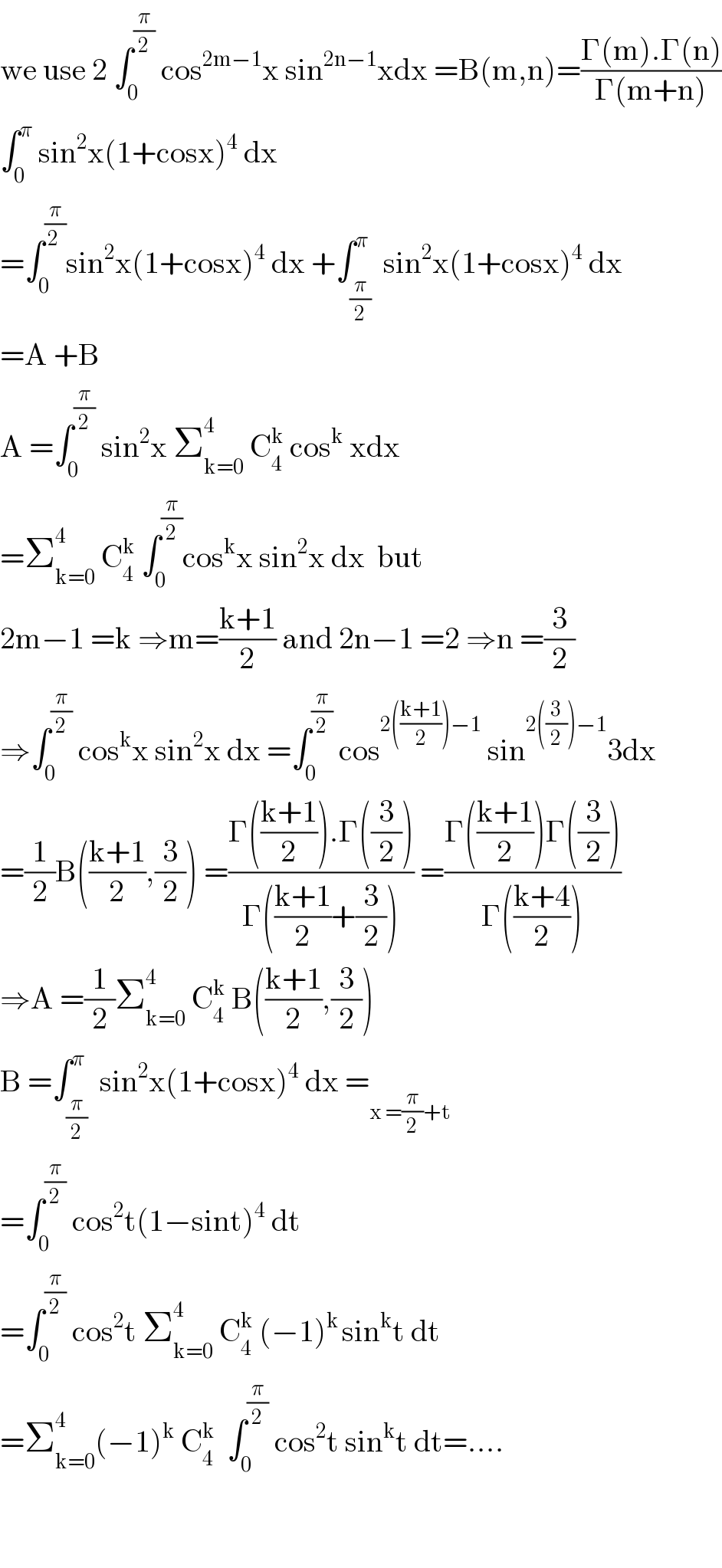
$$\mathrm{we}\:\mathrm{use}\:\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2m}−\mathrm{1}} \mathrm{x}\:\mathrm{sin}^{\mathrm{2n}−\mathrm{1}} \mathrm{xdx}\:=\mathrm{B}\left(\mathrm{m},\mathrm{n}\right)=\frac{\Gamma\left(\mathrm{m}\right).\Gamma\left(\mathrm{n}\right)}{\Gamma\left(\mathrm{m}+\mathrm{n}\right)} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\mathrm{sin}^{\mathrm{2}} \mathrm{x}\left(\mathrm{1}+\mathrm{cosx}\right)^{\mathrm{4}} \:\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}\:}} \mathrm{sin}^{\mathrm{2}} \mathrm{x}\left(\mathrm{1}+\mathrm{cosx}\right)^{\mathrm{4}} \:\mathrm{dx}\:+\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:\mathrm{sin}^{\mathrm{2}} \mathrm{x}\left(\mathrm{1}+\mathrm{cosx}\right)^{\mathrm{4}} \:\mathrm{dx} \\ $$$$=\mathrm{A}\:+\mathrm{B} \\ $$$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{sin}^{\mathrm{2}} \mathrm{x}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4}} \:\mathrm{C}_{\mathrm{4}} ^{\mathrm{k}} \:\mathrm{cos}^{\mathrm{k}} \:\mathrm{xdx} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4}} \:\mathrm{C}_{\mathrm{4}} ^{\mathrm{k}} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{k}} \mathrm{x}\:\mathrm{sin}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx}\:\:\mathrm{but} \\ $$$$\mathrm{2m}−\mathrm{1}\:=\mathrm{k}\:\Rightarrow\mathrm{m}=\frac{\mathrm{k}+\mathrm{1}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{2n}−\mathrm{1}\:=\mathrm{2}\:\Rightarrow\mathrm{n}\:=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{k}} \mathrm{x}\:\mathrm{sin}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2}\left(\frac{\mathrm{k}+\mathrm{1}}{\mathrm{2}}\right)−\mathrm{1}} \:\mathrm{sin}^{\mathrm{2}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\mathrm{1}} \mathrm{3dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{B}\left(\frac{\mathrm{k}+\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}\right)\:=\frac{\Gamma\left(\frac{\mathrm{k}+\mathrm{1}}{\mathrm{2}}\right).\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{k}+\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}}\right)}\:=\frac{\Gamma\left(\frac{\mathrm{k}+\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{k}+\mathrm{4}}{\mathrm{2}}\right)} \\ $$$$\Rightarrow\mathrm{A}\:=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4}} \:\mathrm{C}_{\mathrm{4}} ^{\mathrm{k}} \:\mathrm{B}\left(\frac{\mathrm{k}+\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$\mathrm{B}\:=\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:\mathrm{sin}^{\mathrm{2}} \mathrm{x}\left(\mathrm{1}+\mathrm{cosx}\right)^{\mathrm{4}} \:\mathrm{dx}\:=_{\mathrm{x}\:=\frac{\pi}{\mathrm{2}}+\mathrm{t}} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2}} \mathrm{t}\left(\mathrm{1}−\mathrm{sint}\right)^{\mathrm{4}} \:\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2}} \mathrm{t}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4}} \:\mathrm{C}_{\mathrm{4}} ^{\mathrm{k}} \:\left(−\mathrm{1}\right)^{\mathrm{k}\:} \mathrm{sin}^{\mathrm{k}} \mathrm{t}\:\mathrm{dt} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4}} \left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{4}} ^{\mathrm{k}} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2}} \mathrm{t}\:\mathrm{sin}^{\mathrm{k}} \mathrm{t}\:\mathrm{dt}=…. \\ $$$$ \\ $$$$ \\ $$
Answered by smridha last updated on 24/Jun/20
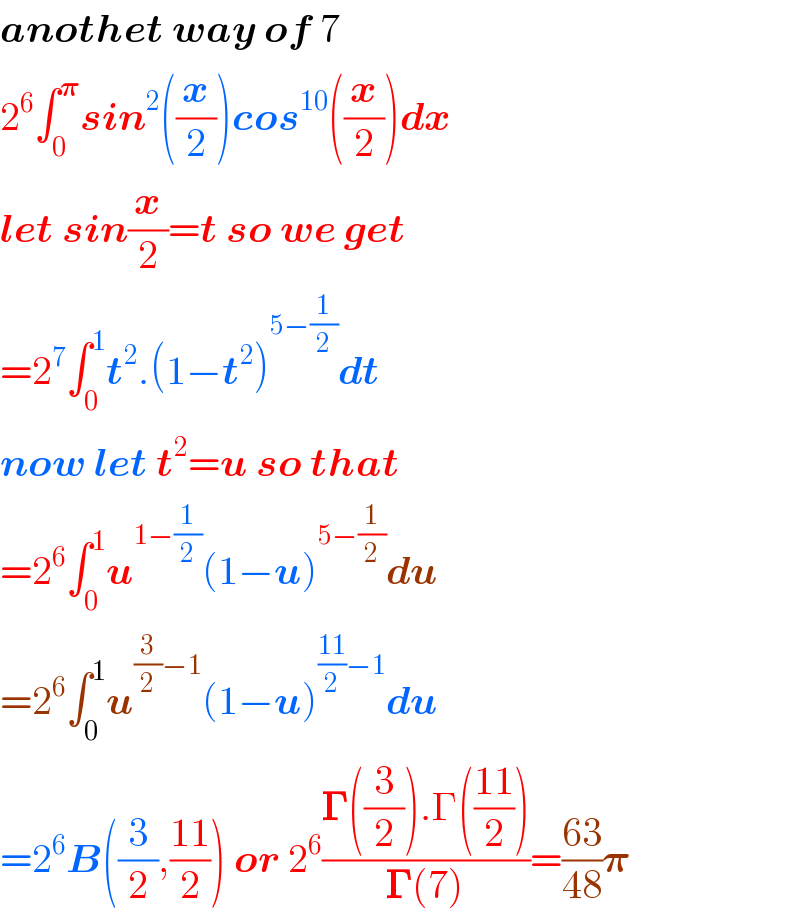
$$\boldsymbol{{anothet}}\:\boldsymbol{{way}}\:\boldsymbol{{of}}\:\mathrm{7} \\ $$$$\mathrm{2}^{\mathrm{6}} \int_{\mathrm{0}} ^{\boldsymbol{\pi}} \boldsymbol{{sin}}^{\mathrm{2}} \left(\frac{\boldsymbol{{x}}}{\mathrm{2}}\right)\boldsymbol{{cos}}^{\mathrm{10}} \left(\frac{\boldsymbol{{x}}}{\mathrm{2}}\right)\boldsymbol{{dx}} \\ $$$$\boldsymbol{{let}}\:\boldsymbol{{sin}}\frac{\boldsymbol{{x}}}{\mathrm{2}}=\boldsymbol{{t}}\:\boldsymbol{{so}}\:\boldsymbol{{we}}\:\boldsymbol{{get}} \\ $$$$=\mathrm{2}^{\mathrm{7}} \int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{{t}}^{\mathrm{2}} .\left(\mathrm{1}−\boldsymbol{{t}}^{\mathrm{2}} \right)^{\mathrm{5}−\frac{\mathrm{1}}{\mathrm{2}}} \boldsymbol{{dt}} \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{let}}\:\boldsymbol{{t}}^{\mathrm{2}} =\boldsymbol{{u}}\:\boldsymbol{{so}}\:\boldsymbol{{that}} \\ $$$$=\mathrm{2}^{\mathrm{6}} \int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{{u}}^{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−\boldsymbol{{u}}\right)^{\mathrm{5}−\frac{\mathrm{1}}{\mathrm{2}}} \boldsymbol{{du}} \\ $$$$=\mathrm{2}^{\mathrm{6}} \int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{{u}}^{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}} \left(\mathrm{1}−\boldsymbol{{u}}\right)^{\frac{\mathrm{11}}{\mathrm{2}}−\mathrm{1}} \boldsymbol{{du}} \\ $$$$=\mathrm{2}^{\mathrm{6}} \boldsymbol{{B}}\left(\frac{\mathrm{3}}{\mathrm{2}},\frac{\mathrm{11}}{\mathrm{2}}\right)\:\boldsymbol{{or}}\:\mathrm{2}^{\mathrm{6}} \frac{\boldsymbol{\Gamma}\left(\frac{\mathrm{3}}{\mathrm{2}}\right).\Gamma\left(\frac{\mathrm{11}}{\mathrm{2}}\right)}{\boldsymbol{\Gamma}\left(\mathrm{7}\right)}=\frac{\mathrm{63}}{\mathrm{48}}\boldsymbol{\pi} \\ $$
Answered by smridha last updated on 24/Jun/20
![8.𝚽=x^3 +y^3 +3xyz−3 ▽𝚽=(3x^2 +3yz)i^� +(3y^2 +3xz)j^� +3xyk^� unit normal vector(1,2,−1) n^� =((▽𝚽)/(∣▽𝚽∣))=((−3i^� +9j^� +6k^� )/( (√((−3)^2 +9^2 +6^2 ))))=(1/( (√(14)))) .[−i^� +3j^� +2k^� ]](https://www.tinkutara.com/question/Q100105.png)
$$\mathrm{8}.\boldsymbol{\Phi}=\boldsymbol{{x}}^{\mathrm{3}} +\boldsymbol{{y}}^{\mathrm{3}} +\mathrm{3}\boldsymbol{{xyz}}−\mathrm{3} \\ $$$$\bigtriangledown\boldsymbol{\Phi}=\left(\mathrm{3}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{3}\boldsymbol{{yz}}\right)\hat {\boldsymbol{{i}}}+\left(\mathrm{3}\boldsymbol{{y}}^{\mathrm{2}} +\mathrm{3}\boldsymbol{{xz}}\right)\hat {\boldsymbol{{j}}}+\mathrm{3}\boldsymbol{{xy}}\hat {\boldsymbol{{k}}} \\ $$$$\boldsymbol{{unit}}\:\boldsymbol{{normal}}\:\boldsymbol{{vector}}\left(\mathrm{1},\mathrm{2},−\mathrm{1}\right) \\ $$$$\hat {\boldsymbol{{n}}}=\frac{\bigtriangledown\boldsymbol{\Phi}}{\mid\bigtriangledown\boldsymbol{\Phi}\mid}=\frac{−\mathrm{3}\hat {{i}}+\mathrm{9}\hat {\boldsymbol{{j}}}+\mathrm{6}\hat {\boldsymbol{{k}}}}{\:\sqrt{\left(−\mathrm{3}\right)^{\mathrm{2}} +\mathrm{9}^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} }}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{14}}}\:.\left[−\hat {\boldsymbol{{i}}}+\mathrm{3}\hat {\boldsymbol{{j}}}+\mathrm{2}\hat {\boldsymbol{{k}}}\right] \\ $$
Answered by smridha last updated on 25/Jun/20
![9)dr of PQ^→ is (4,−2,1) now 𝚽=x^2 −y^2 +2z^2 so the directional derivative is =[▽𝚽]_((1,2,3)) .n^� [where n^� is the unit vector along PQ^→ ] =(2i^� −4j^� +12k^� ).(((4i^� −2j^� +k^� )/( (√(4^2 +(−2)^2 +1^2 ))))) =(1/( (√(21)))).(8+8+12)=((28)/( (√(21))))](https://www.tinkutara.com/question/Q100110.png)
$$\left.\mathrm{9}\right)\boldsymbol{{dr}}\:\boldsymbol{{of}}\:\boldsymbol{{P}}\overset{\rightarrow} {\boldsymbol{{Q}}}\:\boldsymbol{{is}}\:\left(\mathrm{4},−\mathrm{2},\mathrm{1}\right) \\ $$$$\boldsymbol{{now}}\:\boldsymbol{\Phi}=\boldsymbol{{x}}^{\mathrm{2}} −\boldsymbol{{y}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{{z}}^{\mathrm{2}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{the}}\:\boldsymbol{{directional}}\:\boldsymbol{{derivative}}\:\boldsymbol{{is}} \\ $$$$=\left[\bigtriangledown\boldsymbol{\Phi}\right]_{\left(\mathrm{1},\mathrm{2},\mathrm{3}\right)} .\hat {\boldsymbol{{n}}}\left[\boldsymbol{{where}}\:\hat {\boldsymbol{{n}}}\:\boldsymbol{{is}}\:\boldsymbol{{the}}\:\boldsymbol{{unit}}\:\boldsymbol{{vector}}\:\boldsymbol{{along}}\:\boldsymbol{{P}}\overset{\rightarrow} {\boldsymbol{{Q}}}\right] \\ $$$$=\left(\mathrm{2}\hat {\boldsymbol{{i}}}−\mathrm{4}\hat {\boldsymbol{{j}}}+\mathrm{12}\hat {\boldsymbol{{k}}}\right).\left(\frac{\mathrm{4}\hat {\boldsymbol{{i}}}−\mathrm{2}\hat {\boldsymbol{{j}}}+\hat {\boldsymbol{{k}}}}{\:\sqrt{\mathrm{4}^{\mathrm{2}} +\left(−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }}\right) \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{21}}}.\left(\mathrm{8}+\mathrm{8}+\mathrm{12}\right)=\frac{\mathrm{28}}{\:\sqrt{\mathrm{21}}} \\ $$
