Menu Close

Question-100146

Tinku Tara 0 Comments
Pin




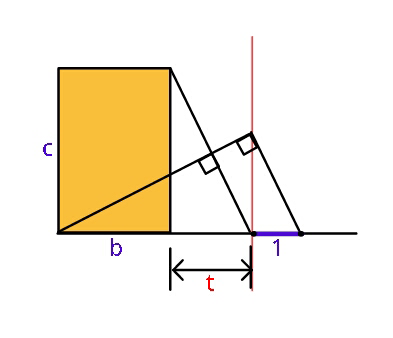
Question Number 100146 by ajfour last updated on 25/Jun/20
Commented by bemath last updated on 25/Jun/20
t = ((c^2 −2b−1)/(2(b+1)))
$$\:\:\:\:\:\:\mathrm{t}\:=\:\frac{\mathrm{c}^{\mathrm{2}} −\mathrm{2b}−\mathrm{1}}{\mathrm{2}\left(\mathrm{b}+\mathrm{1}\right)} \\ $$
Commented by ajfour last updated on 25/Jun/20
clearly (√(b+t))=(c/t) or (b+t)t^2 = c^2 let me check (b+((c^2 −2b−1)/(2(b+1))))[((c^2 −2b−1)/(2(b+1)))]^2 ≠ c^2 please check your answer sir, or post your workings..
$${clearly}\:\:\sqrt{{b}+{t}}=\frac{{c}}{{t}} \\ $$$${or}\:\:\:\left({b}+{t}\right){t}^{\mathrm{2}} =\:{c}^{\mathrm{2}} \\ $$$${let}\:{me}\:{check} \\ $$$$\:\:\:\left({b}+\frac{{c}^{\mathrm{2}} −\mathrm{2}{b}−\mathrm{1}}{\mathrm{2}\left({b}+\mathrm{1}\right)}\right)\left[\frac{{c}^{\mathrm{2}} −\mathrm{2}{b}−\mathrm{1}}{\mathrm{2}\left({b}+\mathrm{1}\right)}\right]^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\neq\:{c}^{\mathrm{2}} \\ $$$${please}\:{check}\:{your}\:{answer}\:{sir}, \\ $$$${or}\:{post}\:{your}\:{workings}.. \\ $$
Commented by ajfour last updated on 25/Jun/20
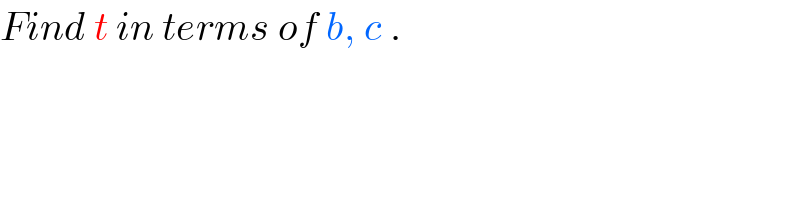
Find t in terms of b, c .
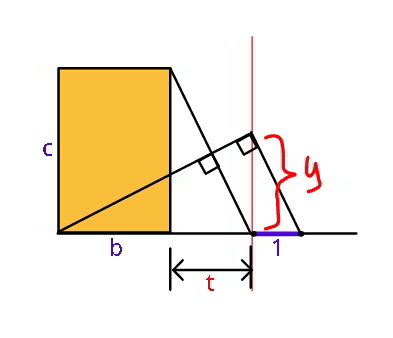
$${Find}\:{t}\:{in}\:{terms}\:{of}\:{b},\:{c}\:. \\ $$
Answered by mr W last updated on 25/Jun/20
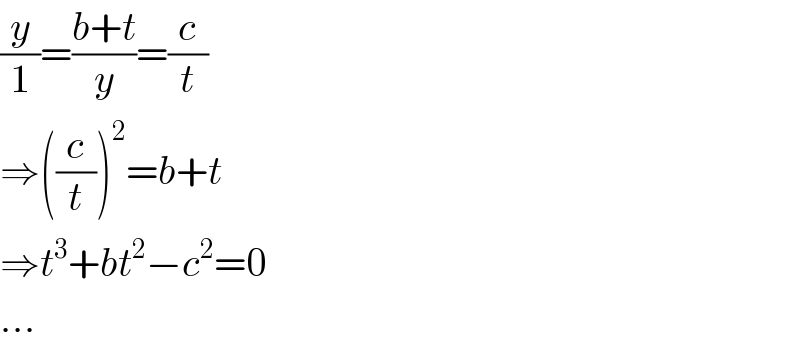
(y/1)=((b+t)/y)=(c/t) ⇒((c/t))^2 =b+t ⇒t^3 +bt^2 −c^2 =0 ...
$$\frac{{y}}{\mathrm{1}}=\frac{{b}+{t}}{{y}}=\frac{{c}}{{t}} \\ $$$$\Rightarrow\left(\frac{{c}}{{t}}\right)^{\mathrm{2}} ={b}+{t} \\ $$$$\Rightarrow{t}^{\mathrm{3}} +{bt}^{\mathrm{2}} −{c}^{\mathrm{2}} =\mathrm{0} \\ $$$$… \\ $$
Commented by ajfour last updated on 25/Jun/20
thanls sir, i hope someday some geometry shall pave the way..!
$${thanls}\:{sir},\:{i}\:{hope}\:{someday} \\ $$$${some}\:{geometry}\:{shall}\:{pave}\:{the} \\ $$$${way}..! \\ $$
Commented by bemath last updated on 25/Jun/20
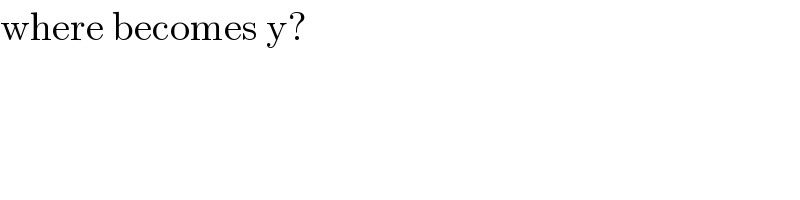
where becomes y?
$$\mathrm{where}\:\mathrm{becomes}\:\mathrm{y}? \\ $$
Commented by 1549442205 last updated on 25/Jun/20
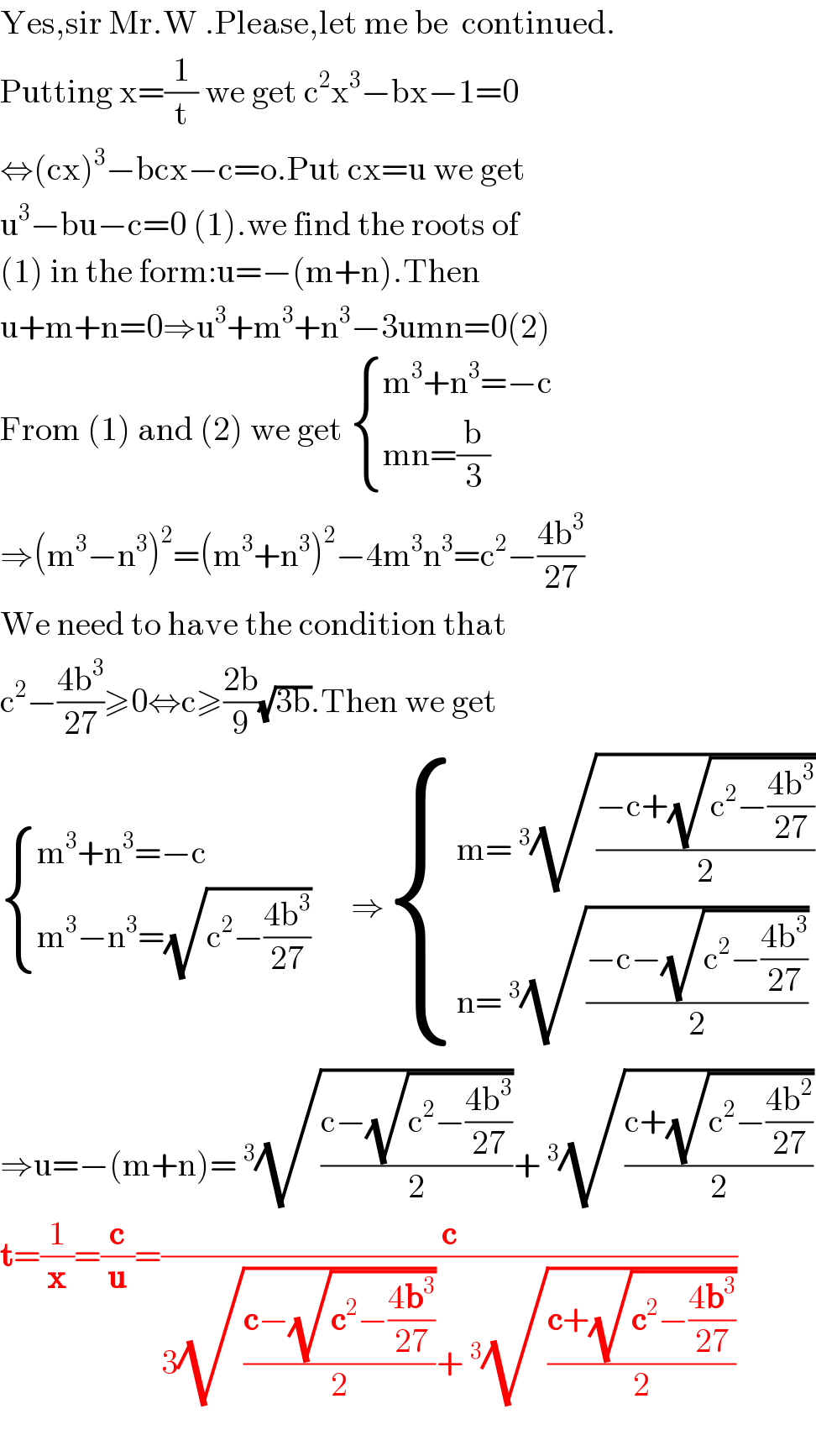
Yes,sir Mr.W .Please,let me be continued. Putting x=(1/t) we get c^2 x^3 −bx−1=0 ⇔(cx)^3 −bcx−c=o.Put cx=u we get u^3 −bu−c=0 (1).we find the roots of (1) in the form:u=−(m+n).Then u+m+n=0⇒u^3 +m^3 +n^3 −3umn=0(2) From (1) and (2) we get { ((m^3 +n^3 =−c)),((mn=(b/3))) :} ⇒(m^3 −n^3 )^2 =(m^3 +n^3 )^2 −4m^3 n^3 =c^2 −((4b^3 )/(27)) We need to have the condition that c^2 −((4b^3 )/(27))≥0⇔c≥((2b)/9)(√(3b)).Then we get { ((m^3 +n^3 =−c)),((m^3 −n^3 =(√(c^2 −((4b^3 )/(27)))))) :} ⇒ { ((m=^3 (√((−c+(√(c^2 −((4b^3 )/(27)))))/2)))),((n=^3 (√((−c−(√(c^2 −((4b^3 )/(27)))))/2)))) :} ⇒u=−(m+n)=^3 (√((c−(√(c^2 −((4b^3 )/(27)))))/2))+^3 (√((c+(√(c^2 −((4b^2 )/(27)))))/2)) t=(1/x)=(c/u)=(c/(3(√((c−(√(c^2 −((4b^3 )/(27)))))/2))+^3 (√((c+(√(c^2 −((4b^3 )/(27)))))/2))))
$$\mathrm{Yes},\mathrm{sir}\:\mathrm{Mr}.\mathrm{W}\:.\mathrm{Please},\mathrm{let}\:\mathrm{me}\:\mathrm{be}\:\:\mathrm{continued}. \\ $$$$\mathrm{Putting}\:\mathrm{x}=\frac{\mathrm{1}}{\mathrm{t}}\:\mathrm{we}\:\mathrm{get}\:\mathrm{c}^{\mathrm{2}} \mathrm{x}^{\mathrm{3}} −\mathrm{bx}−\mathrm{1}=\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{cx}\right)^{\mathrm{3}} −\mathrm{bcx}−\mathrm{c}=\mathrm{o}.\mathrm{Put}\:\mathrm{cx}=\mathrm{u}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{u}^{\mathrm{3}} −\mathrm{bu}−\mathrm{c}=\mathrm{0}\:\left(\mathrm{1}\right).\mathrm{we}\:\mathrm{find}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\: \\ $$$$\left(\mathrm{1}\right)\:\mathrm{in}\:\mathrm{the}\:\mathrm{form}:\mathrm{u}=−\left(\mathrm{m}+\mathrm{n}\right).\mathrm{Then} \\ $$$$\mathrm{u}+\mathrm{m}+\mathrm{n}=\mathrm{0}\Rightarrow\mathrm{u}^{\mathrm{3}} +\mathrm{m}^{\mathrm{3}} +\mathrm{n}^{\mathrm{3}} −\mathrm{3umn}=\mathrm{0}\left(\mathrm{2}\right) \\ $$$$\mathrm{From}\:\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right)\:\mathrm{we}\:\mathrm{get}\:\begin{cases}{\mathrm{m}^{\mathrm{3}} +\mathrm{n}^{\mathrm{3}} =−\mathrm{c}}\\{\mathrm{mn}=\frac{\mathrm{b}}{\mathrm{3}}}\end{cases} \\ $$$$\Rightarrow\left(\mathrm{m}^{\mathrm{3}} −\mathrm{n}^{\mathrm{3}} \right)^{\mathrm{2}} =\left(\mathrm{m}^{\mathrm{3}} +\mathrm{n}^{\mathrm{3}} \right)^{\mathrm{2}} −\mathrm{4m}^{\mathrm{3}} \mathrm{n}^{\mathrm{3}} =\mathrm{c}^{\mathrm{2}} −\frac{\mathrm{4b}^{\mathrm{3}} }{\mathrm{27}} \\ $$$$\mathrm{We}\:\mathrm{need}\:\mathrm{to}\:\mathrm{have}\:\mathrm{the}\:\mathrm{condition}\:\mathrm{that} \\ $$$$\mathrm{c}^{\mathrm{2}} −\frac{\mathrm{4b}^{\mathrm{3}} }{\mathrm{27}}\geqslant\mathrm{0}\Leftrightarrow\mathrm{c}\geqslant\frac{\mathrm{2b}}{\mathrm{9}}\sqrt{\mathrm{3b}}.\mathrm{Then}\:\mathrm{we}\:\mathrm{get} \\ $$$$\begin{cases}{\mathrm{m}^{\mathrm{3}} +\mathrm{n}^{\mathrm{3}} =−\mathrm{c}}\\{\mathrm{m}^{\mathrm{3}} −\mathrm{n}^{\mathrm{3}} =\sqrt{\mathrm{c}^{\mathrm{2}} −\frac{\mathrm{4b}^{\mathrm{3}} }{\mathrm{27}}}}\end{cases}\:\:\:\:\:\:\Rightarrow\begin{cases}{\mathrm{m}=\:^{\mathrm{3}} \sqrt{\frac{−\mathrm{c}+\sqrt{\mathrm{c}^{\mathrm{2}} −\frac{\mathrm{4b}^{\mathrm{3}} }{\mathrm{27}}}}{\mathrm{2}}}}\\{\mathrm{n}=\:^{\mathrm{3}} \sqrt{\frac{−\mathrm{c}−\sqrt{\mathrm{c}^{\mathrm{2}} −\frac{\mathrm{4b}^{\mathrm{3}} }{\mathrm{27}}}}{\mathrm{2}}}}\end{cases} \\ $$$$\Rightarrow\mathrm{u}=−\left(\mathrm{m}+\mathrm{n}\right)=\:^{\mathrm{3}} \sqrt{\frac{\mathrm{c}−\sqrt{\mathrm{c}^{\mathrm{2}} −\frac{\mathrm{4b}^{\mathrm{3}} }{\mathrm{27}}}}{\mathrm{2}}}+\:^{\mathrm{3}} \sqrt{\frac{\mathrm{c}+\sqrt{\mathrm{c}^{\mathrm{2}} −\frac{\mathrm{4b}^{\mathrm{2}} }{\mathrm{27}}}}{\mathrm{2}}} \\ $$$$\boldsymbol{\mathrm{t}}=\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}=\frac{\boldsymbol{\mathrm{c}}}{\boldsymbol{\mathrm{u}}}=\frac{\boldsymbol{\mathrm{c}}}{\mathrm{3}\sqrt{\frac{\boldsymbol{\mathrm{c}}−\sqrt{\boldsymbol{\mathrm{c}}^{\mathrm{2}} −\frac{\mathrm{4}\boldsymbol{\mathrm{b}}^{\mathrm{3}} }{\mathrm{27}}}}{\mathrm{2}}}+\:^{\mathrm{3}} \sqrt{\frac{\boldsymbol{\mathrm{c}}+\sqrt{\boldsymbol{\mathrm{c}}^{\mathrm{2}} −\frac{\mathrm{4}\boldsymbol{\mathrm{b}}^{\mathrm{3}} }{\mathrm{27}}}}{\mathrm{2}}}} \\ $$$$ \\ $$
Commented by mr W last updated on 25/Jun/20
thank you, very nice sir! i have had applied cardano directly.
$${thank}\:{you},\:{very}\:{nice}\:{sir}! \\ $$$${i}\:{have}\:{had}\:{applied}\:{cardano}\:{directly}. \\ $$
Commented by mr W last updated on 25/Jun/20
Commented by ajfour last updated on 25/Jun/20
thanks ....205 Sir, but cannot we have an answer for any real b amd c ?
$${thanks}\:\:….\mathrm{205}\:{Sir},\:{but}\:{cannot} \\ $$$${we}\:{have}\:{an}\:{answer}\:{for}\:{any} \\ $$$${real}\:{b}\:{amd}\:{c}\:? \\ $$
Commented by 1549442205 last updated on 26/Jun/20
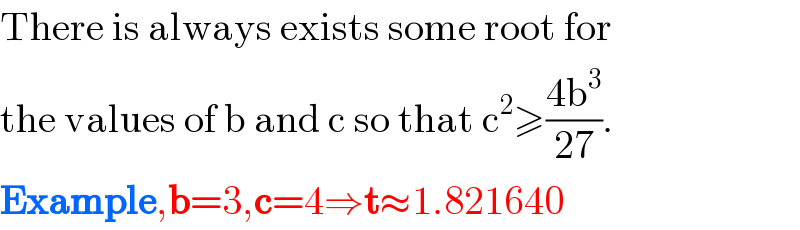
There is always exists some root for the values of b and c so that c^2 ≥((4b^3 )/(27)). Example,b=3,c=4⇒t≈1.821640
$$\mathrm{There}\:\mathrm{is}\:\mathrm{always}\:\mathrm{exists}\:\mathrm{some}\:\mathrm{root}\:\mathrm{for}\: \\ $$$$\mathrm{the}\:\mathrm{values}\:\mathrm{of}\:\mathrm{b}\:\mathrm{and}\:\mathrm{c}\:\mathrm{so}\:\mathrm{that}\:\mathrm{c}^{\mathrm{2}} \geqslant\frac{\mathrm{4b}^{\mathrm{3}} }{\mathrm{27}}. \\ $$$$\boldsymbol{\mathrm{Example}},\boldsymbol{\mathrm{b}}=\mathrm{3},\boldsymbol{\mathrm{c}}=\mathrm{4}\Rightarrow\boldsymbol{\mathrm{t}}\approx\mathrm{1}.\mathrm{821640} \\ $$
Commented by 1549442205 last updated on 30/Jun/20
But I want(please get his permission) to do the his work again in...the moment!.!.!
$$\mathrm{But}\:\mathrm{I}\:\mathrm{want}\left(\mathrm{please}\:\mathrm{get}\:\mathrm{his}\:\mathrm{permission}\right)\: \\ $$$$\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{do}}\:\mathrm{the}\:\mathrm{his}\:\mathrm{work}\: \\ $$$$\mathrm{again}\:\mathrm{in}…\mathrm{the}\:\mathrm{moment}!.!.! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *