Question Number 100223 by DGmichael last updated on 25/Jun/20
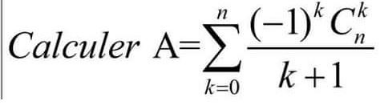
Answered by maths mind last updated on 25/Jun/20
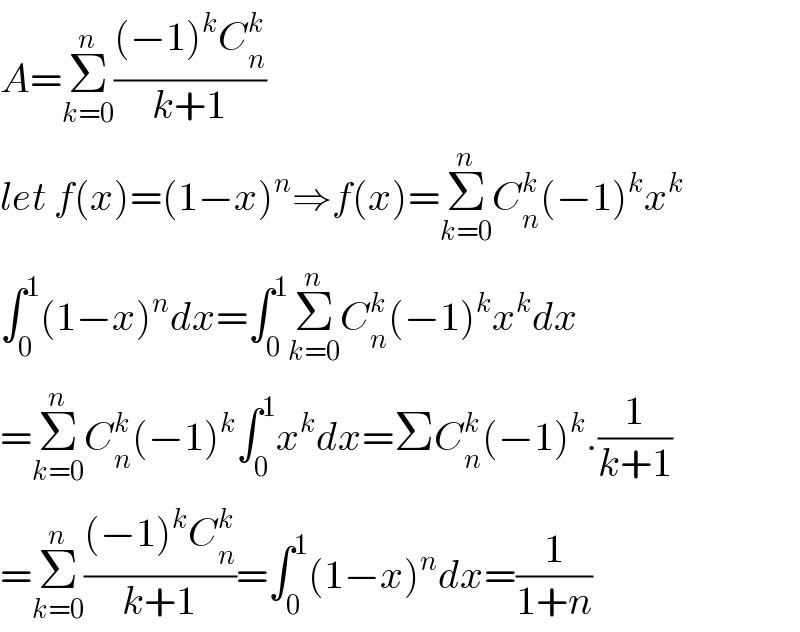
$${A}=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} {C}_{{n}} ^{{k}} }{{k}+\mathrm{1}} \\ $$$${let}\:{f}\left({x}\right)=\left(\mathrm{1}−{x}\right)^{{n}} \Rightarrow{f}\left({x}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} \left(−\mathrm{1}\right)^{{k}} {x}^{{k}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{n}} {dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} \left(−\mathrm{1}\right)^{{k}} {x}^{{k}} {dx} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} \left(−\mathrm{1}\right)^{{k}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{k}} {dx}=\Sigma{C}_{{n}} ^{{k}} \left(−\mathrm{1}\right)^{{k}} .\frac{\mathrm{1}}{{k}+\mathrm{1}} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} {C}_{{n}} ^{{k}} }{{k}+\mathrm{1}}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{n}} {dx}=\frac{\mathrm{1}}{\mathrm{1}+{n}} \\ $$
Commented by Ar Brandon last updated on 25/Jun/20
wow amazing ! you quickly recognized the integral.��
Commented by Ar Brandon last updated on 25/Jun/20
Excuse me Sir, Is there any theory for this, or any particular topic that deals with these kind of sums ?
Commented by maths mind last updated on 25/Jun/20

$${the}\:{main}\:{idea} \\ $$$${is}\:{newtoon}\:{identitie} \\ $$$$\left({x}+{y}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} {x}^{{k}} {y}^{{n}−{k}} \\ $$$${then}\:{use}\:{it}\:{integral}\:{or}\:{differebtial} \\ $$$$\partial_{{x}} \left({x}+{y}\right)^{{n}} =\partial_{{x}} \underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} {x}^{{k}} {y}^{{n}−{k}} \Leftrightarrow{n}\left({x}+{y}\right)^{{n}−\mathrm{1}} =\underset{{k}\geqslant\mathrm{1}} {\sum}{C}_{{n}} ^{{k}} {kx}^{{k}−\mathrm{1}} {y}^{{n}−{k}} \\ $$$${or}\:\frac{\left({x}+{y}\right)^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}=\Sigma{C}_{{n}} ^{{k}} \frac{{x}^{{k}+\mathrm{1}} {y}^{{n}−{k}} }{{k}+\mathrm{1}} \\ $$$${exempl}\: \\ $$$${we}\:{want} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{C}_{{n}} ^{{k}} }{\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)\left({k}+\mathrm{3}\right)}… \\ $$$$\left(\mathrm{1}+{x}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} {x}^{{k}} \Rightarrow\int_{\mathrm{0}} ^{{t}} \left(\mathrm{1}+{x}\right)^{{n}} {dx}=\Sigma\int_{\mathrm{0}} ^{{t}} {C}_{{n}} ^{{k}} {x}^{{k}} {dx} \\ $$$$\Rightarrow\frac{\left(\mathrm{1}+{t}\right)^{{n}} −\mathrm{1}}{{n}+\mathrm{1}}=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{C}_{{n}} ^{{k}} {t}^{{k}+\mathrm{1}} }{{k}+\mathrm{1}} \\ $$$$\int_{\mathrm{0}} ^{{x}} \frac{\left(\mathrm{1}+{t}\right)^{{n}} −\mathrm{1}}{\left({n}+\mathrm{1}\right)}{dt}=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} \int_{\mathrm{0}} ^{{x}} \frac{{t}^{{k}+\mathrm{1}} }{\left({k}+\mathrm{1}\right)}{dt}=\Sigma{C}_{{n}} ^{{k}} \frac{{x}^{{k}+\mathrm{2}} }{\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)} \\ $$$$\frac{\left(\mathrm{1}+{x}\right)^{{n}+\mathrm{2}} }{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}−\frac{{x}}{{n}+\mathrm{1}}=\Sigma{C}_{{n}} ^{{k}} \frac{{x}^{{k}+\mathrm{2}} }{\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{{y}} \frac{\left(\mathrm{1}+{x}\right)^{{n}+\mathrm{2}} }{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}−\frac{{x}}{{n}+\mathrm{1}}=\Sigma{C}_{{n}} ^{{k}} \int_{\mathrm{0}} ^{{y}} \frac{{x}^{{k}+\mathrm{2}} }{\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)} \\ $$$$\Leftrightarrow\frac{\left(\mathrm{1}+{y}\right)^{{n}+\mathrm{3}} }{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)}−\frac{{y}^{\mathrm{2}} }{\mathrm{2}\left({n}+\mathrm{1}\right)}=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} \frac{{y}^{{k}+\mathrm{3}} }{\left({k}+\mathrm{2}\right)\left({k}+\mathrm{1}\right)\left({k}+\mathrm{3}\right)} \\ $$$${y}=\mathrm{1}\Leftrightarrow\frac{\mathrm{2}^{{n}+\mathrm{3}} }{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)}−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)}−\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} .\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)\left({k}+\mathrm{3}\right)} \\ $$$${we}\:{can}\:{Show} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{C}_{{n}} ^{{k}} }{\underset{{b}=\mathrm{1}} {\overset{{r}} {\prod}}\left({k}+{b}\right)}=\frac{\mathrm{2}^{{r}+{n}} }{\left({n}+\mathrm{1}\right)…..\left({n}+{r}\right)}−\underset{{j}=\mathrm{1}} {\overset{{r}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{\left({r}−{j}\right)!\underset{{k}=\mathrm{1}} {\overset{{j}} {\prod}}\left({n}+{j}\right)} \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 26/Jun/20
Thanks a lot for your time Sir��
Commented by DGmichael last updated on 26/Jun/20
�� thanks dear sir!
