Question Number 100304 by Algoritm last updated on 26/Jun/20

Commented by PRITHWISH SEN 2 last updated on 26/Jun/20

$$\mathrm{t}_{\mathrm{n}} =\frac{\mathrm{n}}{\left(\mathrm{n}+\mathrm{1}\right)!}\:=\:\frac{\mathrm{1}}{\mathrm{n}!}\:−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)!}\: \\ $$$$\mathrm{and}\:\mathrm{it}\:\mathrm{is}\:\mathrm{a}\:\mathrm{telescopic}\:\mathrm{series} \\ $$
Commented by Dwaipayan Shikari last updated on 26/Jun/20
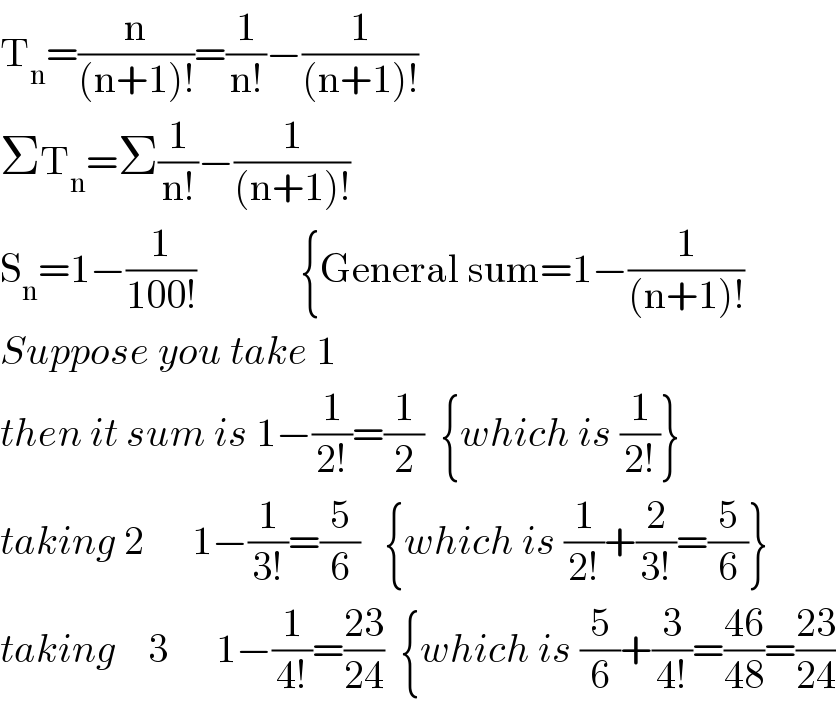
$$\mathrm{T}_{\mathrm{n}} =\frac{\mathrm{n}}{\left(\mathrm{n}+\mathrm{1}\right)!}=\frac{\mathrm{1}}{\mathrm{n}!}−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)!} \\ $$$$\Sigma\mathrm{T}_{\mathrm{n}} =\Sigma\frac{\mathrm{1}}{\mathrm{n}!}−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)!} \\ $$$$\mathrm{S}_{\mathrm{n}} =\mathrm{1}−\frac{\mathrm{1}}{\mathrm{100}!}\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{\mathrm{General}\:\mathrm{sum}=\mathrm{1}−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)!}\right. \\ $$$${Suppose}\:{you}\:{take}\:\mathrm{1} \\ $$$${then}\:{it}\:{sum}\:{is}\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}!}=\frac{\mathrm{1}}{\mathrm{2}}\:\:\left\{{which}\:{is}\:\frac{\mathrm{1}}{\mathrm{2}!}\right\} \\ $$$${taking}\:\mathrm{2}\:\:\:\:\:\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}!}=\frac{\mathrm{5}}{\mathrm{6}}\:\:\:\left\{{which}\:{is}\:\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{2}}{\mathrm{3}!}=\frac{\mathrm{5}}{\mathrm{6}}\right\} \\ $$$${taking}\:\:\:\:\mathrm{3}\:\:\:\:\:\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}!}=\frac{\mathrm{23}}{\mathrm{24}}\:\:\left\{{which}\:{is}\:\frac{\mathrm{5}}{\mathrm{6}}+\frac{\mathrm{3}}{\mathrm{4}!}=\frac{\mathrm{46}}{\mathrm{48}}=\frac{\mathrm{23}}{\mathrm{24}}\right. \\ $$
Commented by PRITHWISH SEN 2 last updated on 26/Jun/20

$$\mathrm{I}\:\mathrm{think}\:\mathrm{you}\:\mathrm{have}\:\mathrm{to}\:\mathrm{start}\:\mathrm{from}\:\mathrm{n}=\mathrm{2}.\:\mathrm{Now}\:\mathrm{do}\:\mathrm{it}. \\ $$
