Menu Close

Question-100311

Tinku Tara 0 Comments
Pin




Question Number 100311 by mathocean1 last updated on 26/Jun/20
Answered by mathmax by abdo last updated on 26/Jun/20
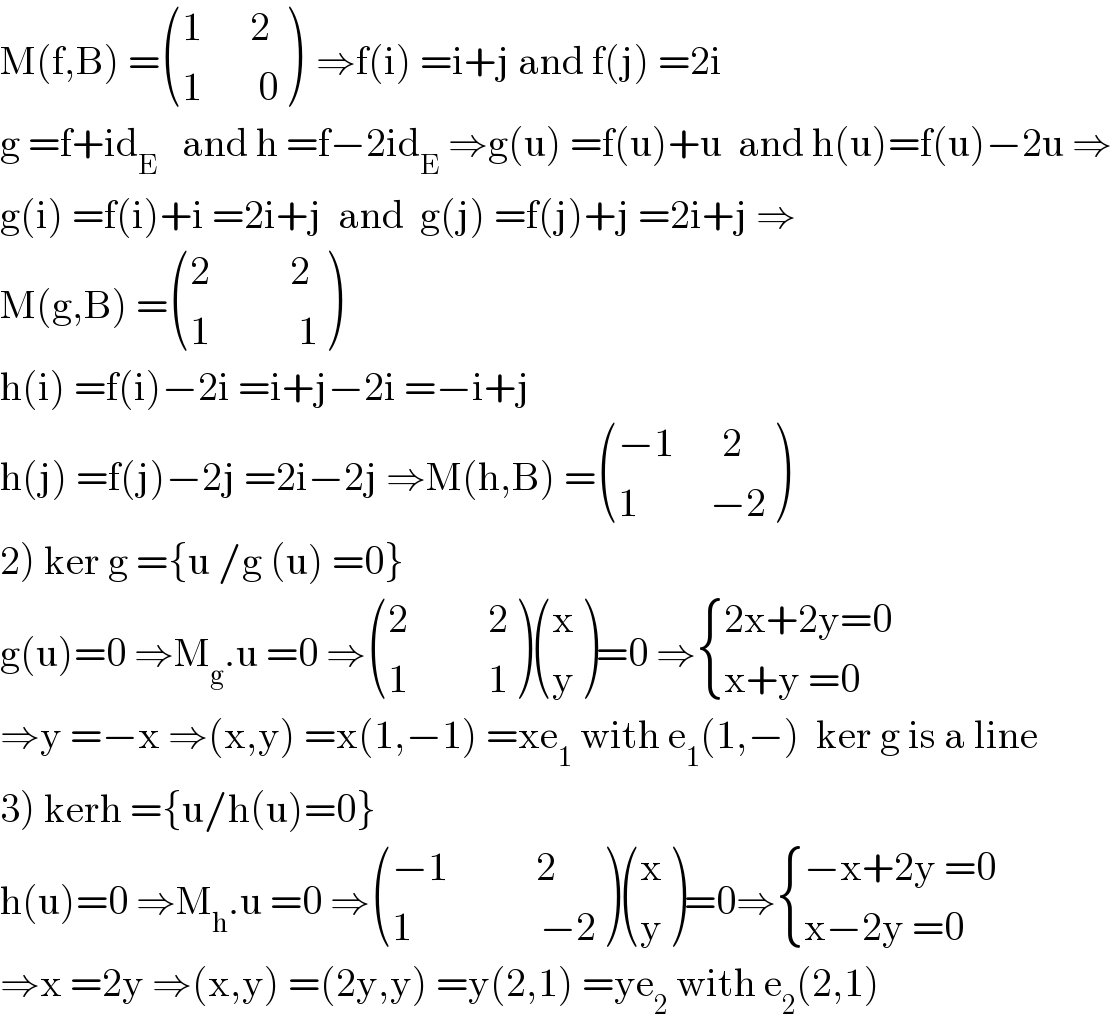
M(f,B) = (((1 2)),((1 0)) ) ⇒f(i) =i+j and f(j) =2i g =f+id_E and h =f−2id_E ⇒g(u) =f(u)+u and h(u)=f(u)−2u ⇒ g(i) =f(i)+i =2i+j and g(j) =f(j)+j =2i+j ⇒ M(g,B) = (((2 2)),((1 1)) ) h(i) =f(i)−2i =i+j−2i =−i+j h(j) =f(j)−2j =2i−2j ⇒M(h,B) = (((−1 2)),((1 −2)) ) 2) ker g ={u /g (u) =0} g(u)=0 ⇒M_g .u =0 ⇒ (((2 2)),((1 1)) ) ((x),(y) )=0 ⇒ { ((2x+2y=0)),((x+y =0)) :} ⇒y =−x ⇒(x,y) =x(1,−1) =xe_1 with e_1 (1,−) ker g is a line 3) kerh ={u/h(u)=0} h(u)=0 ⇒M_h .u =0 ⇒ (((−1 2)),((1 −2)) ) ((x),(y) )=0⇒ { ((−x+2y =0)),((x−2y =0)) :} ⇒x =2y ⇒(x,y) =(2y,y) =y(2,1) =ye_2 with e_2 (2,1)
$$\mathrm{M}\left(\mathrm{f},\mathrm{B}\right)\:=\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\mathrm{2}}\\{\mathrm{1}\:\:\:\:\:\:\:\mathrm{0}}\end{pmatrix}\:\:\Rightarrow\mathrm{f}\left(\mathrm{i}\right)\:=\mathrm{i}+\mathrm{j}\:\mathrm{and}\:\mathrm{f}\left(\mathrm{j}\right)\:=\mathrm{2i} \\ $$$$\mathrm{g}\:=\mathrm{f}+\mathrm{id}_{\mathrm{E}} \:\:\:\mathrm{and}\:\mathrm{h}\:=\mathrm{f}−\mathrm{2id}_{\mathrm{E}} \:\Rightarrow\mathrm{g}\left(\mathrm{u}\right)\:=\mathrm{f}\left(\mathrm{u}\right)+\mathrm{u}\:\:\mathrm{and}\:\mathrm{h}\left(\mathrm{u}\right)=\mathrm{f}\left(\mathrm{u}\right)−\mathrm{2u}\:\Rightarrow \\ $$$$\mathrm{g}\left(\mathrm{i}\right)\:=\mathrm{f}\left(\mathrm{i}\right)+\mathrm{i}\:=\mathrm{2i}+\mathrm{j}\:\:\mathrm{and}\:\:\mathrm{g}\left(\mathrm{j}\right)\:=\mathrm{f}\left(\mathrm{j}\right)+\mathrm{j}\:=\mathrm{2i}+\mathrm{j}\:\Rightarrow \\ $$$$\mathrm{M}\left(\mathrm{g},\mathrm{B}\right)\:=\begin{pmatrix}{\mathrm{2}\:\:\:\:\:\:\:\:\:\:\mathrm{2}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$\mathrm{h}\left(\mathrm{i}\right)\:=\mathrm{f}\left(\mathrm{i}\right)−\mathrm{2i}\:=\mathrm{i}+\mathrm{j}−\mathrm{2i}\:=−\mathrm{i}+\mathrm{j} \\ $$$$\mathrm{h}\left(\mathrm{j}\right)\:=\mathrm{f}\left(\mathrm{j}\right)−\mathrm{2j}\:=\mathrm{2i}−\mathrm{2j}\:\Rightarrow\mathrm{M}\left(\mathrm{h},\mathrm{B}\right)\:=\begin{pmatrix}{−\mathrm{1}\:\:\:\:\:\:\mathrm{2}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:−\mathrm{2}}\end{pmatrix} \\ $$$$\left.\mathrm{2}\right)\:\mathrm{ker}\:\mathrm{g}\:=\left\{\mathrm{u}\:/\mathrm{g}\:\left(\mathrm{u}\right)\:=\mathrm{0}\right\} \\ $$$$\mathrm{g}\left(\mathrm{u}\right)=\mathrm{0}\:\Rightarrow\mathrm{M}_{\mathrm{g}} .\mathrm{u}\:=\mathrm{0}\:\Rightarrow\begin{pmatrix}{\mathrm{2}\:\:\:\:\:\:\:\:\:\:\mathrm{2}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}\begin{pmatrix}{\mathrm{x}}\\{\mathrm{y}}\end{pmatrix}=\mathrm{0}\:\Rightarrow\begin{cases}{\mathrm{2x}+\mathrm{2y}=\mathrm{0}}\\{\mathrm{x}+\mathrm{y}\:=\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\mathrm{y}\:=−\mathrm{x}\:\Rightarrow\left(\mathrm{x},\mathrm{y}\right)\:=\mathrm{x}\left(\mathrm{1},−\mathrm{1}\right)\:=\mathrm{xe}_{\mathrm{1}} \:\mathrm{with}\:\mathrm{e}_{\mathrm{1}} \left(\mathrm{1},−\right)\:\:\mathrm{ker}\:\mathrm{g}\:\mathrm{is}\:\mathrm{a}\:\mathrm{line} \\ $$$$\left.\mathrm{3}\right)\:\mathrm{kerh}\:=\left\{\mathrm{u}/\mathrm{h}\left(\mathrm{u}\right)=\mathrm{0}\right\} \\ $$$$\mathrm{h}\left(\mathrm{u}\right)=\mathrm{0}\:\Rightarrow\mathrm{M}_{\mathrm{h}} .\mathrm{u}\:=\mathrm{0}\:\Rightarrow\begin{pmatrix}{−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2}}\end{pmatrix}\begin{pmatrix}{\mathrm{x}}\\{\mathrm{y}}\end{pmatrix}=\mathrm{0}\Rightarrow\begin{cases}{−\mathrm{x}+\mathrm{2y}\:=\mathrm{0}}\\{\mathrm{x}−\mathrm{2y}\:=\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\mathrm{x}\:=\mathrm{2y}\:\Rightarrow\left(\mathrm{x},\mathrm{y}\right)\:=\left(\mathrm{2y},\mathrm{y}\right)\:=\mathrm{y}\left(\mathrm{2},\mathrm{1}\right)\:=\mathrm{ye}_{\mathrm{2}} \:\mathrm{with}\:\mathrm{e}_{\mathrm{2}} \left(\mathrm{2},\mathrm{1}\right) \\ $$
Commented by mathocean1 last updated on 26/Jun/20
Thank you very much sir! It is too great... May God bless you
$${Thank}\:{you}\:{very}\:{much}\:{sir}! \\ $$$${It}\:{is}\:{too}\:{great}…\:{May}\:\:{God}\:{bless}\:{you} \\ $$
Commented by mathmax by abdo last updated on 26/Jun/20
you are welcome.
$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *