Question Number 100330 by bemath last updated on 26/Jun/20
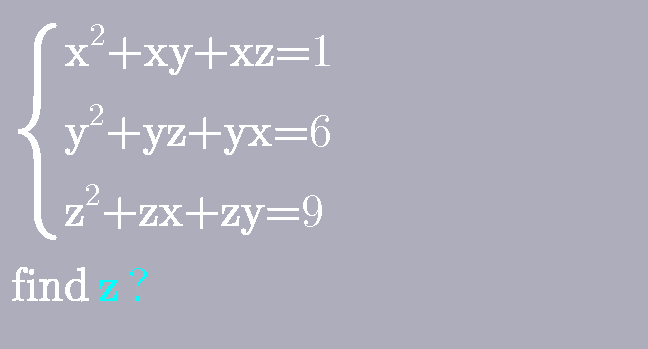
Commented by bobhans last updated on 26/Jun/20
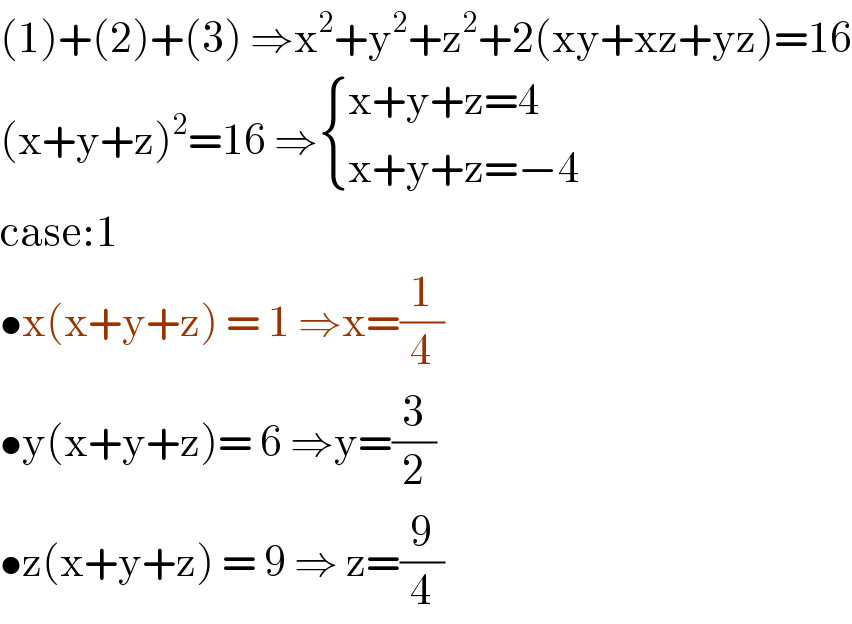
$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)+\left(\mathrm{3}\right)\:\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{xy}+\mathrm{xz}+\mathrm{yz}\right)=\mathrm{16} \\ $$$$\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)^{\mathrm{2}} =\mathrm{16}\:\Rightarrow\begin{cases}{\mathrm{x}+\mathrm{y}+\mathrm{z}=\mathrm{4}}\\{\mathrm{x}+\mathrm{y}+\mathrm{z}=−\mathrm{4}}\end{cases} \\ $$$$\mathrm{case}:\mathrm{1}\: \\ $$$$\bullet\mathrm{x}\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)\:=\:\mathrm{1}\:\Rightarrow\mathrm{x}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\bullet\mathrm{y}\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)=\:\mathrm{6}\:\Rightarrow\mathrm{y}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\bullet\mathrm{z}\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)\:=\:\mathrm{9}\:\Rightarrow\:\mathrm{z}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$
