Menu Close

Question-100404

Tinku Tara 0 Comments
Pin




Question Number 100404 by PengagumRahasiamu last updated on 26/Jun/20
Commented by PengagumRahasiamu last updated on 26/Jun/20
Thank you
Commented by Rasheed.Sindhi last updated on 26/Jun/20
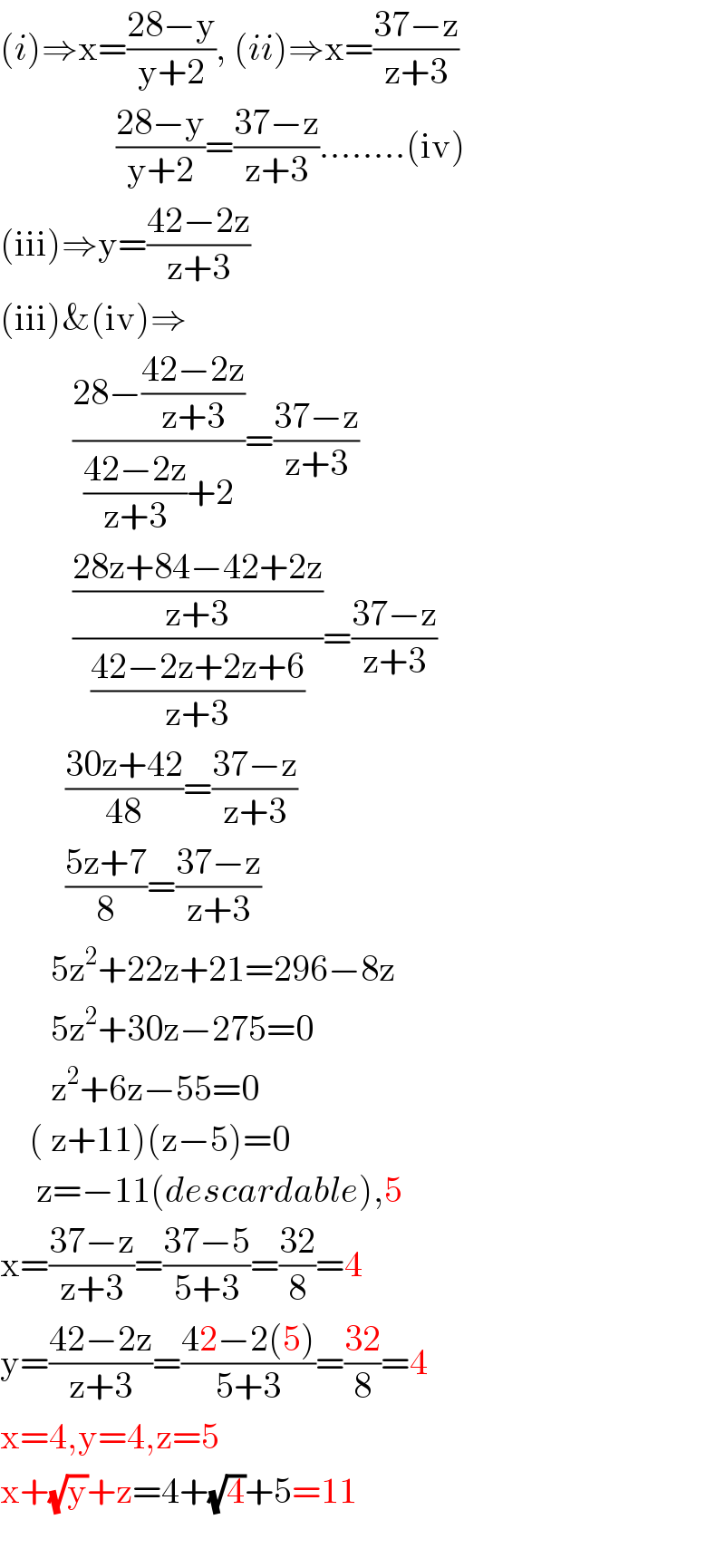
(i)⇒x=((28−y)/(y+2)), (ii)⇒x=((37−z)/(z+3)) ((28−y)/(y+2))=((37−z)/(z+3))........(iv) (iii)⇒y=((42−2z)/(z+3)) (iii)&(iv)⇒ ((28−((42−2z)/(z+3)))/(((42−2z)/(z+3))+2))=((37−z)/(z+3)) (((28z+84−42+2z)/(z+3))/((42−2z+2z+6)/(z+3)))=((37−z)/(z+3)) ((30z+42)/(48))=((37−z)/(z+3)) ((5z+7)/8)=((37−z)/(z+3)) 5z^2 +22z+21=296−8z 5z^2 +30z−275=0 z^2 +6z−55=0 ( z+11)(z−5)=0 z=−11(descardable),5 x=((37−z)/(z+3))=((37−5)/(5+3))=((32)/8)=4 y=((42−2z)/(z+3))=((42−2(5))/(5+3))=((32)/8)=4 x=4,y=4,z=5 x+(√y)+z=4+(√4)+5=11
$$\left({i}\right)\Rightarrow\mathrm{x}=\frac{\mathrm{28}−\mathrm{y}}{\mathrm{y}+\mathrm{2}},\:\left({ii}\right)\Rightarrow\mathrm{x}=\frac{\mathrm{37}−\mathrm{z}}{\mathrm{z}+\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{28}−\mathrm{y}}{\mathrm{y}+\mathrm{2}}=\frac{\mathrm{37}−\mathrm{z}}{\mathrm{z}+\mathrm{3}}……..\left(\mathrm{iv}\right) \\ $$$$\left(\mathrm{iii}\right)\Rightarrow\mathrm{y}=\frac{\mathrm{42}−\mathrm{2z}}{\mathrm{z}+\mathrm{3}} \\ $$$$\left(\mathrm{iii}\right)\&\left(\mathrm{iv}\right)\Rightarrow \\ $$$$\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{28}−\frac{\mathrm{42}−\mathrm{2z}}{\mathrm{z}+\mathrm{3}}}{\frac{\mathrm{42}−\mathrm{2z}}{\mathrm{z}+\mathrm{3}}+\mathrm{2}}=\frac{\mathrm{37}−\mathrm{z}}{\mathrm{z}+\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\frac{\frac{\mathrm{28z}+\mathrm{84}−\mathrm{42}+\mathrm{2z}}{\mathrm{z}+\mathrm{3}}}{\frac{\mathrm{42}−\mathrm{2z}+\mathrm{2z}+\mathrm{6}}{\mathrm{z}+\mathrm{3}}}=\frac{\mathrm{37}−\mathrm{z}}{\mathrm{z}+\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\frac{\mathrm{30z}+\mathrm{42}}{\mathrm{48}}=\frac{\mathrm{37}−\mathrm{z}}{\mathrm{z}+\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\frac{\mathrm{5z}+\mathrm{7}}{\mathrm{8}}=\frac{\mathrm{37}−\mathrm{z}}{\mathrm{z}+\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\mathrm{5z}^{\mathrm{2}} +\mathrm{22z}+\mathrm{21}=\mathrm{296}−\mathrm{8z} \\ $$$$\:\:\:\:\:\:\:\mathrm{5z}^{\mathrm{2}} +\mathrm{30z}−\mathrm{275}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\mathrm{z}^{\mathrm{2}} +\mathrm{6z}−\mathrm{55}=\mathrm{0} \\ $$$$\:\:\:\:\left(\:\mathrm{z}+\mathrm{11}\right)\left(\mathrm{z}−\mathrm{5}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{z}=−\mathrm{11}\left({descardable}\right),\mathrm{5} \\ $$$$\mathrm{x}=\frac{\mathrm{37}−\mathrm{z}}{\mathrm{z}+\mathrm{3}}=\frac{\mathrm{37}−\mathrm{5}}{\mathrm{5}+\mathrm{3}}=\frac{\mathrm{32}}{\mathrm{8}}=\mathrm{4} \\ $$$$\mathrm{y}=\frac{\mathrm{42}−\mathrm{2z}}{\mathrm{z}+\mathrm{3}}=\frac{\mathrm{42}−\mathrm{2}\left(\mathrm{5}\right)}{\mathrm{5}+\mathrm{3}}=\frac{\mathrm{32}}{\mathrm{8}}=\mathrm{4} \\ $$$$\mathrm{x}=\mathrm{4},\mathrm{y}=\mathrm{4},\mathrm{z}=\mathrm{5} \\ $$$$\mathrm{x}+\sqrt{\mathrm{y}}+\mathrm{z}=\mathrm{4}+\sqrt{\mathrm{4}}+\mathrm{5}=\mathrm{11} \\ $$$$\:\:\: \\ $$
Commented by bobhans last updated on 27/Jun/20
x= ((28−y)/(y+2)) = ((37−z)/(z+3)) ∧ y= ((42−2z)/(z+3)) ((28−(((42−2z)/(z+3))))/(((42−2z)/(z+3)) +2)) = ((37−z)/(z+3)) ⇒ ((30z+42)/((z+3)(48))) = ((37−z)/(z+3)) ((30z+42)/(48)) = ((37−z)/(z+3)) ⇒(5z+7)(z+3) = 296−8z 5z^2 +22z+21=296−8z 5z^2 +30z−275=0, z^2 +6z−55=0 (z+11)(z−5)=0 ⇒ { ((z=5)),((y=((42−10)/8)= 4)),((x=((28−4)/6)=4)) :} ∴ x+(√y) +z = 4+2+5 = 11 ■
$$\mathrm{x}=\:\frac{\mathrm{28}−\mathrm{y}}{\mathrm{y}+\mathrm{2}}\:=\:\frac{\mathrm{37}−\mathrm{z}}{\mathrm{z}+\mathrm{3}}\:\wedge\:\mathrm{y}=\:\frac{\mathrm{42}−\mathrm{2z}}{\mathrm{z}+\mathrm{3}} \\ $$$$\frac{\mathrm{28}−\left(\frac{\mathrm{42}−\mathrm{2z}}{\mathrm{z}+\mathrm{3}}\right)}{\frac{\mathrm{42}−\mathrm{2z}}{\mathrm{z}+\mathrm{3}}\:+\mathrm{2}}\:=\:\frac{\mathrm{37}−\mathrm{z}}{\mathrm{z}+\mathrm{3}}\:\Rightarrow\:\frac{\mathrm{30z}+\mathrm{42}}{\left(\mathrm{z}+\mathrm{3}\right)\left(\mathrm{48}\right)}\:=\:\frac{\mathrm{37}−\mathrm{z}}{\mathrm{z}+\mathrm{3}} \\ $$$$\frac{\mathrm{30z}+\mathrm{42}}{\mathrm{48}}\:=\:\frac{\mathrm{37}−\mathrm{z}}{\mathrm{z}+\mathrm{3}}\:\Rightarrow\left(\mathrm{5z}+\mathrm{7}\right)\left(\mathrm{z}+\mathrm{3}\right)\:=\:\mathrm{296}−\mathrm{8z} \\ $$$$\mathrm{5z}^{\mathrm{2}} +\mathrm{22z}+\mathrm{21}=\mathrm{296}−\mathrm{8z} \\ $$$$\mathrm{5z}^{\mathrm{2}} +\mathrm{30z}−\mathrm{275}=\mathrm{0},\:\mathrm{z}^{\mathrm{2}} +\mathrm{6z}−\mathrm{55}=\mathrm{0} \\ $$$$\left(\mathrm{z}+\mathrm{11}\right)\left(\mathrm{z}−\mathrm{5}\right)=\mathrm{0}\:\Rightarrow\begin{cases}{\mathrm{z}=\mathrm{5}}\\{\mathrm{y}=\frac{\mathrm{42}−\mathrm{10}}{\mathrm{8}}=\:\mathrm{4}}\\{\mathrm{x}=\frac{\mathrm{28}−\mathrm{4}}{\mathrm{6}}=\mathrm{4}}\end{cases} \\ $$$$\therefore\:\mathrm{x}+\sqrt{\mathrm{y}}\:+\mathrm{z}\:=\:\mathrm{4}+\mathrm{2}+\mathrm{5}\:=\:\mathrm{11}\:\blacksquare \\ $$$$ \\ $$
Commented by Rasheed.Sindhi last updated on 26/Jun/20
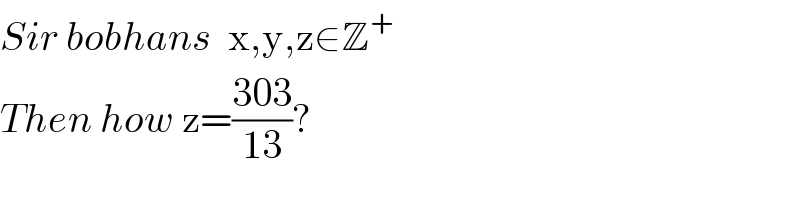
Sir bobhans x,y,z∈Z^+ Then how z=((303)/(13))?
$${Sir}\:{bobhans}\:\:\mathrm{x},\mathrm{y},\mathrm{z}\in\mathbb{Z}^{+} \\ $$$${Then}\:{how}\:\mathrm{z}=\frac{\mathrm{303}}{\mathrm{13}}? \\ $$
Commented by bramlex last updated on 26/Jun/20
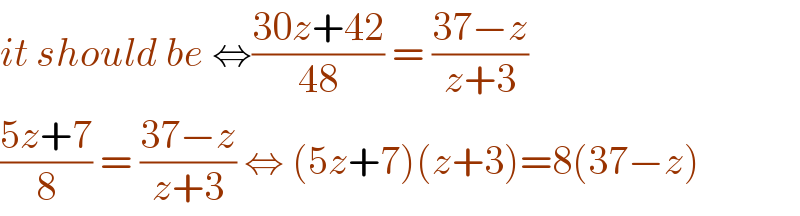
it should be ⇔((30z+42)/(48)) = ((37−z)/(z+3)) ((5z+7)/8) = ((37−z)/(z+3)) ⇔ (5z+7)(z+3)=8(37−z)
$${it}\:{should}\:{be}\:\Leftrightarrow\frac{\mathrm{30}{z}+\mathrm{42}}{\mathrm{48}}\:=\:\frac{\mathrm{37}−{z}}{{z}+\mathrm{3}} \\ $$$$\frac{\mathrm{5}{z}+\mathrm{7}}{\mathrm{8}}\:=\:\frac{\mathrm{37}−{z}}{{z}+\mathrm{3}}\:\Leftrightarrow\:\left(\mathrm{5}{z}+\mathrm{7}\right)\left({z}+\mathrm{3}\right)=\mathrm{8}\left(\mathrm{37}−{z}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 26/Jun/20
x=((28−y)/(y+2)) y=((42−2z)/(z+3)) x=((37−z)/(z+3)) So,((37−z)/(z+3))=((28−((42−2z)/(z+3)))/(((42−2z)/(z+3))+2))⇒((37−z)/(z+3))=((30z+42)/(48)) ((296−8z)/(z+3))=5z+7 ⇒ 296−8z=5z^2 +22z+21 5z^2 +30z−275=0 ⇒z^2 +6z−55 ⇒z=5 or −11 but z≠−11 So; x=4 y=4 so x+(√y)+z=11
$${x}=\frac{\mathrm{28}−{y}}{{y}+\mathrm{2}} \\ $$$${y}=\frac{\mathrm{42}−\mathrm{2}{z}}{{z}+\mathrm{3}} \\ $$$${x}=\frac{\mathrm{37}−{z}}{{z}+\mathrm{3}} \\ $$$$\mathrm{So},\frac{\mathrm{37}−\mathrm{z}}{\mathrm{z}+\mathrm{3}}=\frac{\mathrm{28}−\frac{\mathrm{42}−\mathrm{2z}}{\mathrm{z}+\mathrm{3}}}{\frac{\mathrm{42}−\mathrm{2z}}{\mathrm{z}+\mathrm{3}}+\mathrm{2}}\Rightarrow\frac{\mathrm{37}−\mathrm{z}}{\mathrm{z}+\mathrm{3}}=\frac{\mathrm{30z}+\mathrm{42}}{\mathrm{48}} \\ $$$$\frac{\mathrm{296}−\mathrm{8z}}{\mathrm{z}+\mathrm{3}}=\mathrm{5z}+\mathrm{7}\:\:\:\Rightarrow\:\mathrm{296}−\mathrm{8z}=\mathrm{5z}^{\mathrm{2}} +\mathrm{22z}+\mathrm{21} \\ $$$$\mathrm{5z}^{\mathrm{2}} +\mathrm{30z}−\mathrm{275}=\mathrm{0}\:\:\Rightarrow{z}^{\mathrm{2}} +\mathrm{6}{z}−\mathrm{55}\:\:\:\Rightarrow\mathrm{z}=\mathrm{5}\:\mathrm{or}\:−\mathrm{11}\:\:\mathrm{but}\:\mathrm{z}\neq−\mathrm{11} \\ $$$$\mathrm{So};\:\:\mathrm{x}=\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\mathrm{y}=\mathrm{4} \\ $$$$\mathrm{so}\:\mathrm{x}+\sqrt{\mathrm{y}}+\mathrm{z}=\mathrm{11} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 26/Jun/20
Sir answer will be 11
$$\mathrm{Sir}\:\mathrm{answer}\:\mathrm{will}\:\mathrm{be}\:\mathrm{11} \\ $$
Commented by Dwaipayan Shikari last updated on 26/Jun/20
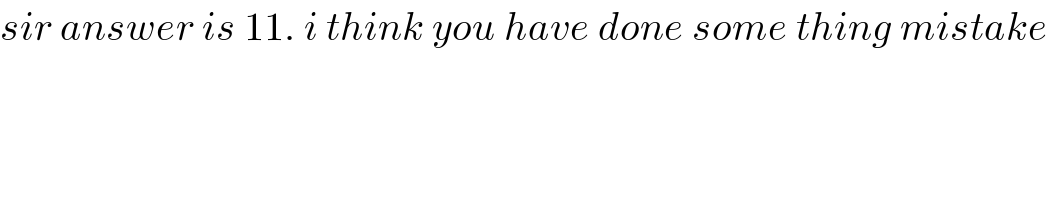
sir answer is 11. i think you have done some thing mistake
$${sir}\:{answer}\:{is}\:\mathrm{11}.\:{i}\:{think}\:{you}\:{have}\:{done}\:{some}\:{thing}\:{mistake} \\ $$
Commented by Dwaipayan Shikari last updated on 26/Jun/20
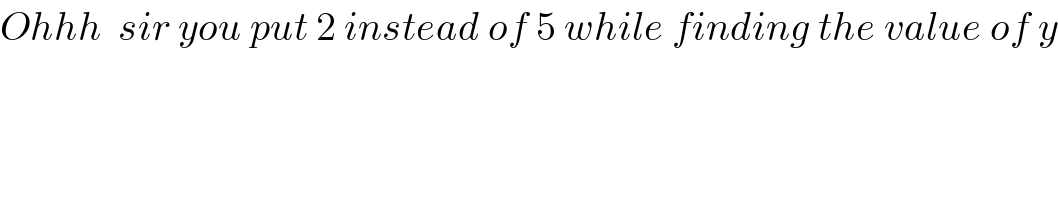
Ohhh sir you put 2 instead of 5 while finding the value of y
$${Ohhh}\:\:{sir}\:{you}\:{put}\:\mathrm{2}\:{instead}\:{of}\:\mathrm{5}\:{while}\:{finding}\:{the}\:{value}\:{of}\:{y} \\ $$
Commented by Rasheed.Sindhi last updated on 26/Jun/20
Thank you sir for mentioning mistake.Now I corrected it.Your answer is also corret.
$$\mathcal{T}{hank}\:{you}\:{sir}\:{for}\:{mentioning} \\ $$$${mistake}.{Now}\:{I}\:{corrected}\:{it}.{Your} \\ $$$${answer}\:{is}\:{also}\:{corret}. \\ $$
Commented by bobhans last updated on 27/Jun/20
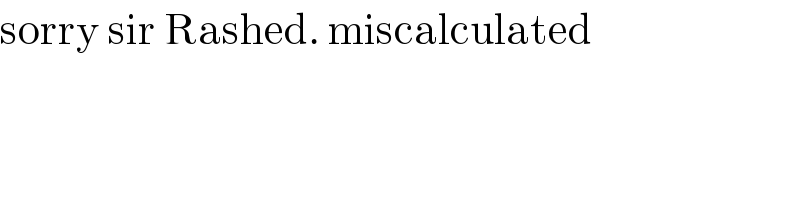
sorry sir Rashed. miscalculated
$$\mathrm{sorry}\:\mathrm{sir}\:\mathrm{Rashed}.\:\mathrm{miscalculated} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *