Question Number 100409 by Algoritm last updated on 26/Jun/20
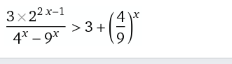
Commented by bramlex last updated on 26/Jun/20
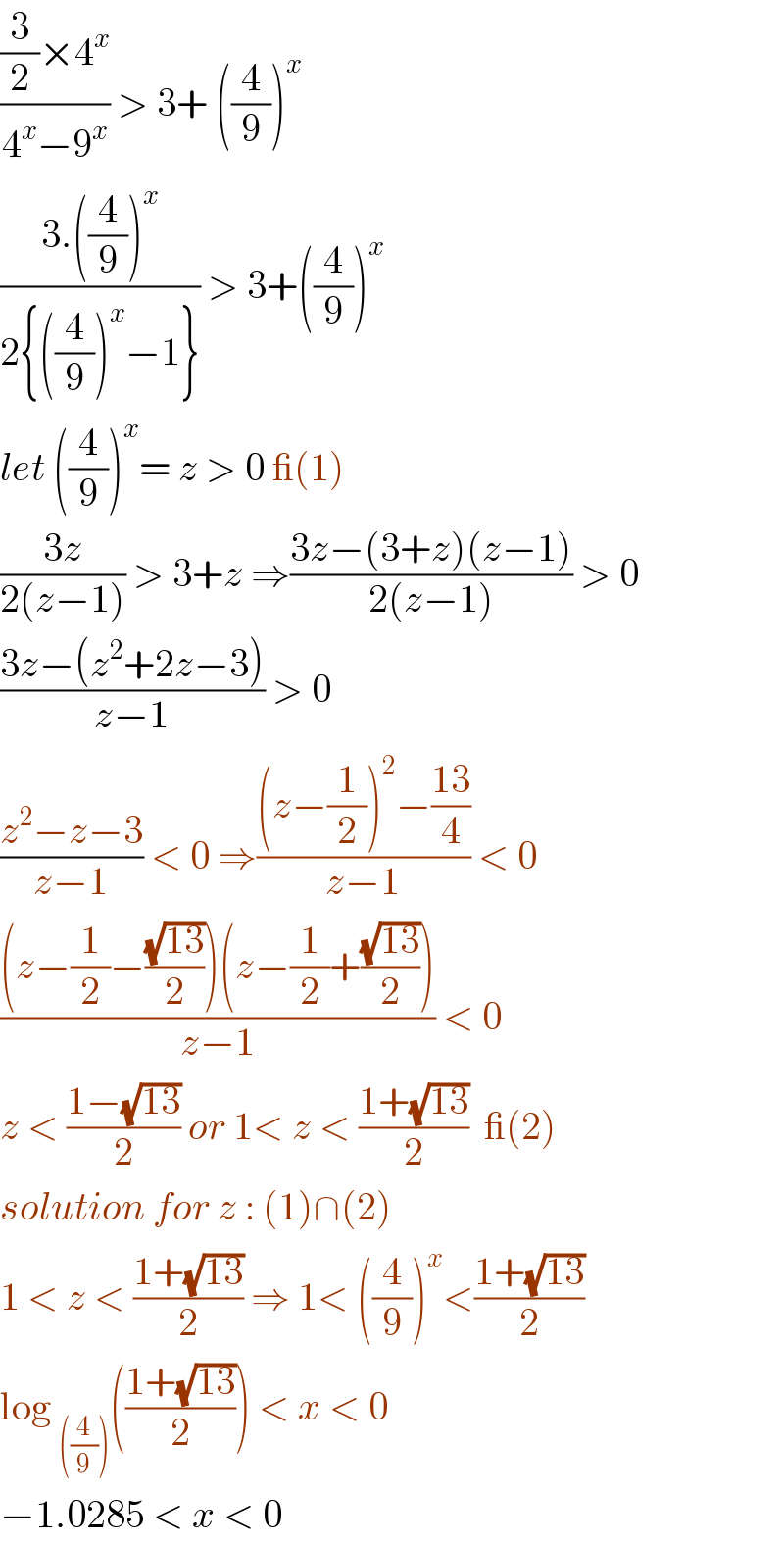
$$\frac{\frac{\mathrm{3}}{\mathrm{2}}×\mathrm{4}^{{x}} }{\mathrm{4}^{{x}} −\mathrm{9}^{{x}} }\:>\:\mathrm{3}+\:\left(\frac{\mathrm{4}}{\mathrm{9}}\right)^{{x}} \\ $$$$\frac{\mathrm{3}.\left(\frac{\mathrm{4}}{\mathrm{9}}\right)^{{x}} }{\mathrm{2}\left\{\left(\frac{\mathrm{4}}{\mathrm{9}}\right)^{{x}} −\mathrm{1}\right\}}\:>\:\mathrm{3}+\left(\frac{\mathrm{4}}{\mathrm{9}}\right)^{{x}} \\ $$$${let}\:\left(\frac{\mathrm{4}}{\mathrm{9}}\right)^{{x}} =\:{z}\:>\:\mathrm{0}\:\_\left(\mathrm{1}\right) \\ $$$$\frac{\mathrm{3}{z}}{\mathrm{2}\left({z}−\mathrm{1}\right)}\:>\:\mathrm{3}+{z}\:\Rightarrow\frac{\mathrm{3}{z}−\left(\mathrm{3}+{z}\right)\left({z}−\mathrm{1}\right)}{\mathrm{2}\left({z}−\mathrm{1}\right)}\:>\:\mathrm{0} \\ $$$$\frac{\mathrm{3}{z}−\left({z}^{\mathrm{2}} +\mathrm{2}{z}−\mathrm{3}\right)}{{z}−\mathrm{1}}\:>\:\mathrm{0} \\ $$$$\frac{{z}^{\mathrm{2}} −{z}−\mathrm{3}}{{z}−\mathrm{1}}\:<\:\mathrm{0}\:\Rightarrow\frac{\left({z}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{13}}{\mathrm{4}}}{{z}−\mathrm{1}}\:<\:\mathrm{0} \\ $$$$\frac{\left({z}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{13}}}{\mathrm{2}}\right)\left({z}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{13}}}{\mathrm{2}}\right)}{{z}−\mathrm{1}}\:<\:\mathrm{0} \\ $$$${z}\:<\:\frac{\mathrm{1}−\sqrt{\mathrm{13}}}{\mathrm{2}}\:{or}\:\mathrm{1}<\:{z}\:<\:\frac{\mathrm{1}+\sqrt{\mathrm{13}}}{\mathrm{2}}\:\:\_\left(\mathrm{2}\right) \\ $$$${solution}\:{for}\:{z}\::\:\left(\mathrm{1}\right)\cap\left(\mathrm{2}\right) \\ $$$$\mathrm{1}\:<\:{z}\:<\:\frac{\mathrm{1}+\sqrt{\mathrm{13}}}{\mathrm{2}}\:\Rightarrow\:\mathrm{1}<\:\left(\frac{\mathrm{4}}{\mathrm{9}}\right)^{{x}} <\frac{\mathrm{1}+\sqrt{\mathrm{13}}}{\mathrm{2}} \\ $$$$\mathrm{log}\:_{\left(\frac{\mathrm{4}}{\mathrm{9}}\right)} \left(\frac{\mathrm{1}+\sqrt{\mathrm{13}}}{\mathrm{2}}\right)\:<\:{x}\:<\:\mathrm{0}\: \\ $$$$−\mathrm{1}.\mathrm{0285}\:<\:{x}\:<\:\mathrm{0}\: \\ $$
Commented by Algoritm last updated on 26/Jun/20

$$ \\ $$
