Menu Close

Question-100543

Tinku Tara 0 Comments
Pin




Question Number 100543 by mhmd last updated on 27/Jun/20
Commented by mr W last updated on 27/Jun/20
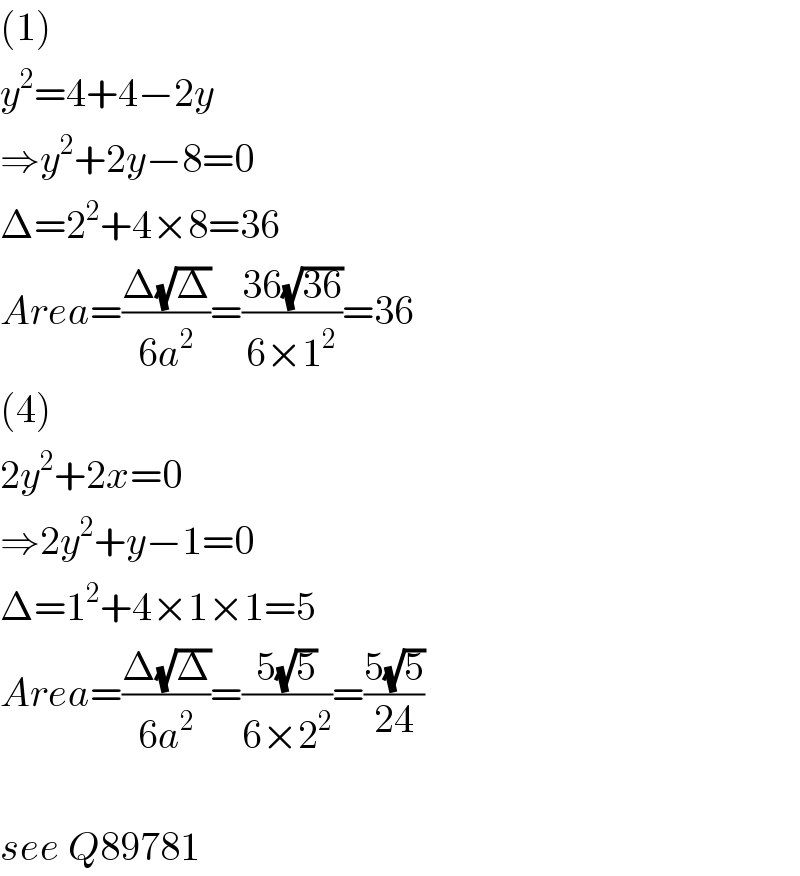
(1) y^2 =4+4−2y ⇒y^2 +2y−8=0 Δ=2^2 +4×8=36 Area=((Δ(√Δ))/(6a^2 ))=((36(√(36)))/(6×1^2 ))=36 (4) 2y^2 +2x=0 ⇒2y^2 +y−1=0 Δ=1^2 +4×1×1=5 Area=((Δ(√Δ))/(6a^2 ))=((5(√5))/(6×2^2 ))=((5(√5))/(24)) see Q89781
$$\left(\mathrm{1}\right) \\ $$$${y}^{\mathrm{2}} =\mathrm{4}+\mathrm{4}−\mathrm{2}{y} \\ $$$$\Rightarrow{y}^{\mathrm{2}} +\mathrm{2}{y}−\mathrm{8}=\mathrm{0} \\ $$$$\Delta=\mathrm{2}^{\mathrm{2}} +\mathrm{4}×\mathrm{8}=\mathrm{36} \\ $$$${Area}=\frac{\Delta\sqrt{\Delta}}{\mathrm{6}{a}^{\mathrm{2}} }=\frac{\mathrm{36}\sqrt{\mathrm{36}}}{\mathrm{6}×\mathrm{1}^{\mathrm{2}} }=\mathrm{36} \\ $$$$\left(\mathrm{4}\right) \\ $$$$\mathrm{2}{y}^{\mathrm{2}} +\mathrm{2}{x}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{y}^{\mathrm{2}} +{y}−\mathrm{1}=\mathrm{0} \\ $$$$\Delta=\mathrm{1}^{\mathrm{2}} +\mathrm{4}×\mathrm{1}×\mathrm{1}=\mathrm{5} \\ $$$${Area}=\frac{\Delta\sqrt{\Delta}}{\mathrm{6}{a}^{\mathrm{2}} }=\frac{\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{6}×\mathrm{2}^{\mathrm{2}} }=\frac{\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{24}} \\ $$$$ \\ $$$${see}\:{Q}\mathrm{89781} \\ $$
Answered by Rio Michael last updated on 27/Jun/20
1 ↘↙ 6 12 2 ↘↙ 4 = 4 −12 −3 ↘↙ 7 = 14 7 1 ↘ ↙ 6 = −18 ⇒ Area of triangle = (1/2)[4 + 14−18 −(12−12 + 7)] = (7/2) square units
$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\searrow\swarrow\:\:\:\mathrm{6} \\ $$$$\:\mathrm{12}\:\:\:\:\:\:\mathrm{2}\:\:\:\:\searrow\swarrow\:\mathrm{4}\:=\:\mathrm{4} \\ $$$$\:−\mathrm{12}\:−\mathrm{3}\:\:\:\searrow\swarrow\:\mathrm{7}\:=\:\mathrm{14} \\ $$$$\:\:\:\:\:\:\:\mathrm{7}\:\:\:\:\:\mathrm{1}\:\:\:\:\searrow\:\swarrow\:\mathrm{6}\:=\:−\mathrm{18} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\Rightarrow\:\mathrm{Area}\:\mathrm{of}\:\mathrm{triangle}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{4}\:+\:\mathrm{14}−\mathrm{18}\:\:−\left(\mathrm{12}−\mathrm{12}\:+\:\mathrm{7}\right)\right]\:=\:\frac{\mathrm{7}}{\mathrm{2}}\:\mathrm{square}\:\mathrm{units} \\ $$
Answered by Rio Michael last updated on 27/Jun/20
Curves intersect at the points (−2,5) , (2.3,0.7) and (1.25,−1.50) ⇒ −2 5 16 2.3 0.7 −1.4 0.851.25 −1.5 3.45 3 −2 5 6.25 A = (1/2)[−1.4+3.45 + 6.25 −(16 + 0.85 + 3)] ≈ 5.78 square units
$$\:\mathrm{Curves}\:\mathrm{intersect}\:\mathrm{at}\:\mathrm{the}\:\mathrm{points}\:\:\left(−\mathrm{2},\mathrm{5}\right)\:,\:\left(\mathrm{2}.\mathrm{3},\mathrm{0}.\mathrm{7}\right)\:\mathrm{and}\:\left(\mathrm{1}.\mathrm{25},−\mathrm{1}.\mathrm{50}\right) \\ $$$$\Rightarrow\:−\mathrm{2}\:\:\:\:\:\:\mathrm{5}\:\: \\ $$$$\:\:\mathrm{16}\:\mathrm{2}.\mathrm{3}\:\:\:\:\:\mathrm{0}.\mathrm{7}\:\:\:\:\:\:−\mathrm{1}.\mathrm{4} \\ $$$$\:\:\:\mathrm{0}.\mathrm{851}.\mathrm{25}\:\:\:\:−\mathrm{1}.\mathrm{5}\:\:\mathrm{3}.\mathrm{45} \\ $$$$\:\:\:\:\:\mathrm{3}\:\:−\mathrm{2}\:\:\:\:\:\:\:\mathrm{5}\:\:\:\:\mathrm{6}.\mathrm{25} \\ $$$${A}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left[−\mathrm{1}.\mathrm{4}+\mathrm{3}.\mathrm{45}\:+\:\mathrm{6}.\mathrm{25}\:−\left(\mathrm{16}\:+\:\mathrm{0}.\mathrm{85}\:+\:\mathrm{3}\right)\right]\:\approx\:\mathrm{5}.\mathrm{78}\:\mathrm{square}\:\mathrm{units} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *