Question Number 100561 by DGmichael last updated on 27/Jun/20

Commented by bramlex last updated on 27/Jun/20
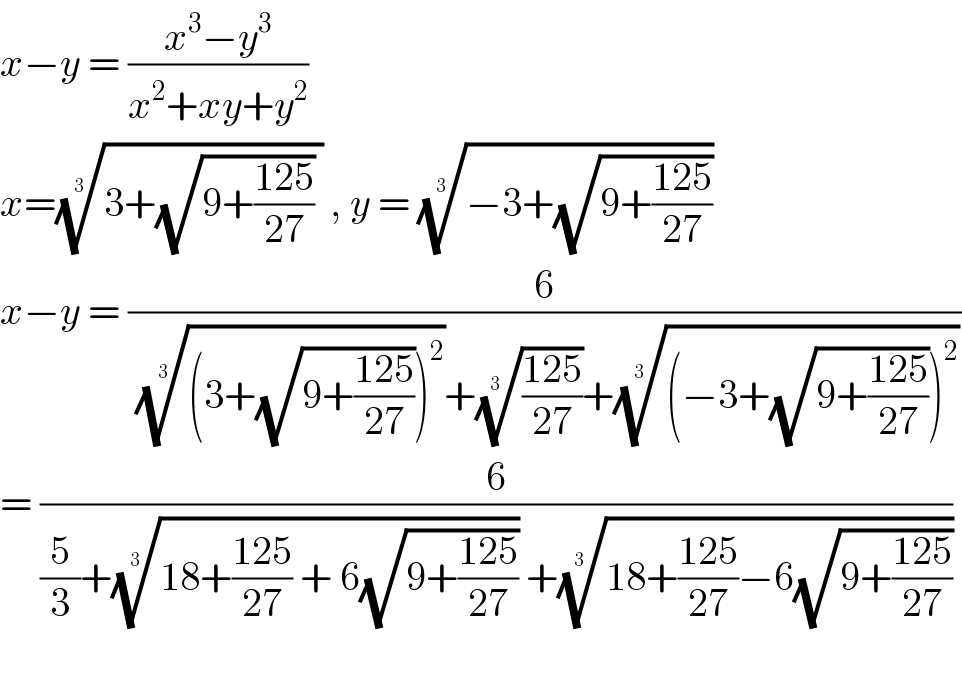
$${x}−{y}\:=\:\frac{{x}^{\mathrm{3}} −{y}^{\mathrm{3}} }{{x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} } \\ $$$${x}=\sqrt[{\mathrm{3}\:}]{\mathrm{3}+\sqrt{\mathrm{9}+\frac{\mathrm{125}}{\mathrm{27}}}\:}\:,\:{y}\:=\:\sqrt[{\mathrm{3}\:}]{−\mathrm{3}+\sqrt{\mathrm{9}+\frac{\mathrm{125}}{\mathrm{27}}}} \\ $$$${x}−{y}\:=\:\frac{\mathrm{6}}{\:\sqrt[{\mathrm{3}\:}]{\left(\mathrm{3}+\sqrt{\mathrm{9}+\frac{\mathrm{125}}{\mathrm{27}}}\right)^{\mathrm{2}} }+\sqrt[{\mathrm{3}\:\:}]{\frac{\mathrm{125}}{\mathrm{27}}}+\sqrt[{\mathrm{3}\:\:}]{\left(−\mathrm{3}+\sqrt{\mathrm{9}+\frac{\mathrm{125}}{\mathrm{27}}}\right)^{\mathrm{2}} }} \\ $$$$=\:\frac{\mathrm{6}}{\frac{\mathrm{5}}{\mathrm{3}}+\sqrt[{\mathrm{3}\:}]{\mathrm{18}+\frac{\mathrm{125}}{\mathrm{27}}\:+\:\mathrm{6}\sqrt{\mathrm{9}+\frac{\mathrm{125}}{\mathrm{27}}}}\:+\sqrt[{\mathrm{3}\:\:}]{\mathrm{18}+\frac{\mathrm{125}}{\mathrm{27}}−\mathrm{6}\sqrt{\mathrm{9}+\frac{\mathrm{125}}{\mathrm{27}}}}} \\ $$$$ \\ $$
Answered by MJS last updated on 27/Jun/20

$${A}\:\mathrm{is}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{of}\:{A}^{\mathrm{3}} +{pA}+{q}=\mathrm{0} \\ $$$$\mathrm{Cardano} \\ $$$${A}=\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}+\sqrt{\frac{{q}^{\mathrm{2}} }{\mathrm{4}}+\frac{{p}^{\mathrm{3}} }{\mathrm{27}}}}+\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}−\sqrt{\frac{{q}^{\mathrm{2}} }{\mathrm{4}}+\frac{{p}^{\mathrm{3}} }{\mathrm{27}}}}= \\ $$$$=\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}+\sqrt{\frac{{q}^{\mathrm{2}} }{\mathrm{4}}+\frac{{p}^{\mathrm{3}} }{\mathrm{27}}}}−\sqrt[{\mathrm{3}}]{\frac{{q}}{\mathrm{2}}+\sqrt{\frac{{q}^{\mathrm{2}} }{\mathrm{4}}+\frac{{p}^{\mathrm{3}} }{\mathrm{27}}}} \\ $$$$\frac{{q}}{\mathrm{2}}=\mathrm{3}\:\Rightarrow\:{q}=\mathrm{6} \\ $$$$\frac{{q}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{9}\:\Rightarrow\:{q}=\pm\mathrm{6} \\ $$$$\Rightarrow\:{q}=\mathrm{6} \\ $$$$\frac{{p}^{\mathrm{3}} }{\mathrm{27}}=\frac{\mathrm{125}}{\mathrm{27}}\:\Rightarrow\:{p}=\mathrm{5} \\ $$$${A}^{\mathrm{3}} +\mathrm{5}{A}+\mathrm{6}=\mathrm{0} \\ $$$$\Rightarrow\:{A}_{\mathrm{1}} =−\mathrm{1}\wedge{A}_{\mathrm{2},\:\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{23}}}{\mathrm{2}}\mathrm{i} \\ $$$$\Rightarrow\:{A}={A}_{\mathrm{1}} =−\mathrm{1} \\ $$
