Question-100565

Question Number 100565 by bemath last updated on 27/Jun/20

Commented by bobhans last updated on 28/Jun/20

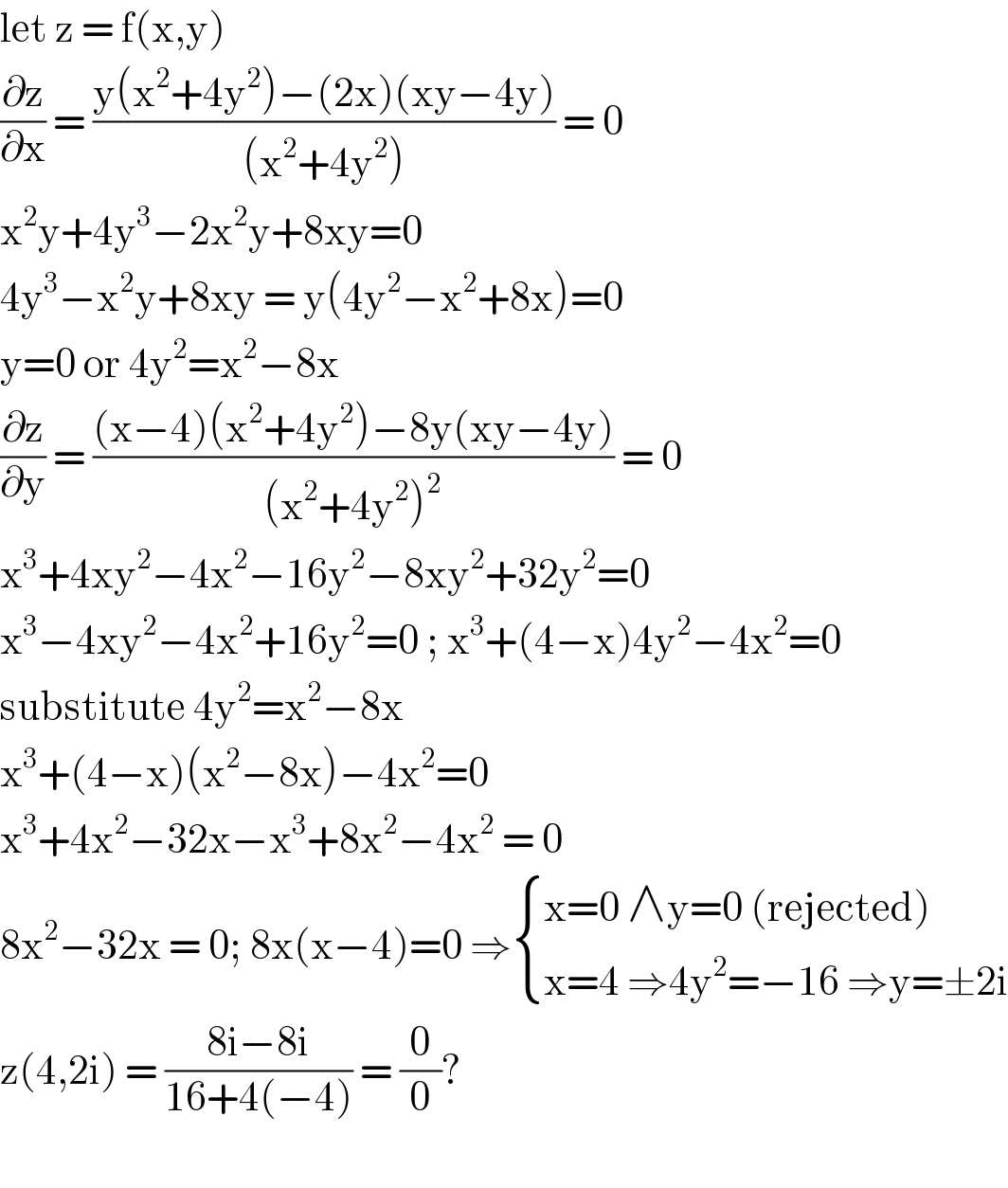
let z = f(x,y) (∂z/∂x) = ((y(x^2 +4y^2 )−(2x)(xy−4y))/((x^2 +4y^2 ))) = 0 x^2 y+4y^3 −2x^2 y+8xy=0 4y^3 −x^2 y+8xy = y(4y^2 −x^2 +8x)=0 y=0 or 4y^2 =x^2 −8x (∂z/∂y) = (((x−4)(x^2 +4y^2 )−8y(xy−4y))/((x^2 +4y^2 )^2 )) = 0 x^3 +4xy^2 −4x^2 −16y^2 −8xy^2 +32y^2 =0 x^3 −4xy^2 −4x^2 +16y^2 =0 ; x^3 +(4−x)4y^2 −4x^2 =0 substitute 4y^2 =x^2 −8x x^3 +(4−x)(x^2 −8x)−4x^2 =0 x^3 +4x^2 −32x−x^3 +8x^2 −4x^2 = 0 8x^2 −32x = 0; 8x(x−4)=0 ⇒ { ((x=0 ∧y=0 (rejected))),((x=4 ⇒4y^2 =−16 ⇒y=±2i)) :} z(4,2i) = ((8i−8i)/(16+4(−4))) = (0/0)?

$$\mathrm{let}\:\mathrm{z}\:=\:\mathrm{f}\left(\mathrm{x},\mathrm{y}\right) \\ $$$$\frac{\partial\mathrm{z}}{\partial\mathrm{x}}\:=\:\frac{\mathrm{y}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4y}^{\mathrm{2}} \right)−\left(\mathrm{2x}\right)\left(\mathrm{xy}−\mathrm{4y}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4y}^{\mathrm{2}} \right)}\:=\:\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} \mathrm{y}+\mathrm{4y}^{\mathrm{3}} −\mathrm{2x}^{\mathrm{2}} \mathrm{y}+\mathrm{8xy}=\mathrm{0} \\ $$$$\mathrm{4y}^{\mathrm{3}} −\mathrm{x}^{\mathrm{2}} \mathrm{y}+\mathrm{8xy}\:=\:\mathrm{y}\left(\mathrm{4y}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} +\mathrm{8x}\right)=\mathrm{0} \\ $$$$\mathrm{y}=\mathrm{0}\:\mathrm{or}\:\mathrm{4y}^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} −\mathrm{8x} \\ $$$$\frac{\partial\mathrm{z}}{\partial\mathrm{y}}\:=\:\frac{\left(\mathrm{x}−\mathrm{4}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4y}^{\mathrm{2}} \right)−\mathrm{8y}\left(\mathrm{xy}−\mathrm{4y}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4y}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\:\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{3}} +\mathrm{4xy}^{\mathrm{2}} −\mathrm{4x}^{\mathrm{2}} −\mathrm{16y}^{\mathrm{2}} −\mathrm{8xy}^{\mathrm{2}} +\mathrm{32y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{3}} −\mathrm{4xy}^{\mathrm{2}} −\mathrm{4x}^{\mathrm{2}} +\mathrm{16y}^{\mathrm{2}} =\mathrm{0}\:;\:\mathrm{x}^{\mathrm{3}} +\left(\mathrm{4}−\mathrm{x}\right)\mathrm{4y}^{\mathrm{2}} −\mathrm{4x}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{substitute}\:\mathrm{4y}^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} −\mathrm{8x} \\ $$$$\mathrm{x}^{\mathrm{3}} +\left(\mathrm{4}−\mathrm{x}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{8x}\right)−\mathrm{4x}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{3}} +\mathrm{4x}^{\mathrm{2}} −\mathrm{32x}−\mathrm{x}^{\mathrm{3}} +\mathrm{8x}^{\mathrm{2}} −\mathrm{4x}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\mathrm{8x}^{\mathrm{2}} −\mathrm{32x}\:=\:\mathrm{0};\:\mathrm{8x}\left(\mathrm{x}−\mathrm{4}\right)=\mathrm{0}\:\Rightarrow\begin{cases}{\mathrm{x}=\mathrm{0}\:\wedge\mathrm{y}=\mathrm{0}\:\left(\mathrm{rejected}\right)}\\{\mathrm{x}=\mathrm{4}\:\Rightarrow\mathrm{4y}^{\mathrm{2}} =−\mathrm{16}\:\Rightarrow\mathrm{y}=\pm\mathrm{2i}}\end{cases} \\ $$$$\mathrm{z}\left(\mathrm{4},\mathrm{2i}\right)\:=\:\frac{\mathrm{8i}−\mathrm{8i}}{\mathrm{16}+\mathrm{4}\left(−\mathrm{4}\right)}\:=\:\frac{\mathrm{0}}{\mathrm{0}}?\: \\ $$$$ \\ $$

Answered by MJS last updated on 27/Jun/20

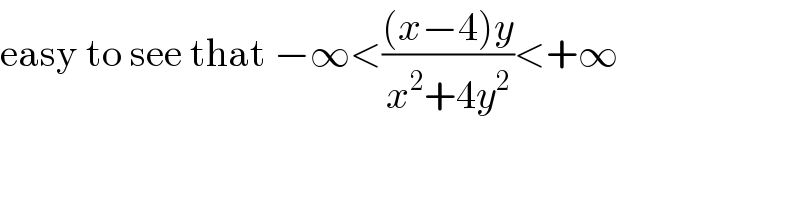
easy to see that −∞<(((x−4)y)/(x^2 +4y^2 ))<+∞

$$\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{that}\:−\infty<\frac{\left({x}−\mathrm{4}\right){y}}{{x}^{\mathrm{2}} +\mathrm{4}{y}^{\mathrm{2}} }<+\infty \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply