Question-100597

Question Number 100597 by bobhans last updated on 27/Jun/20

Commented by Dwaipayan Shikari last updated on 27/Jun/20

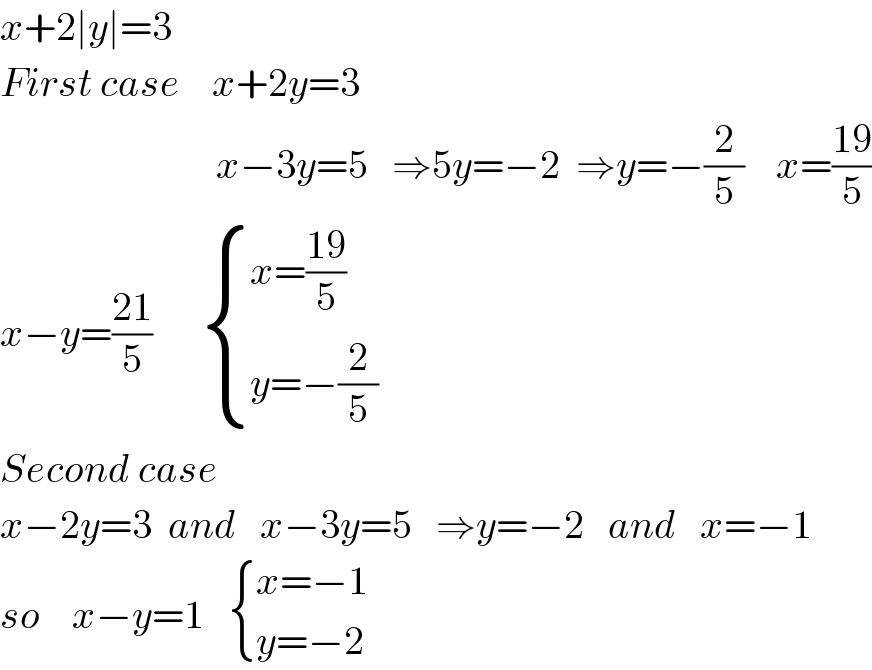
x+2∣y∣=3 First case x+2y=3 x−3y=5 ⇒5y=−2 ⇒y=−(2/5) x=((19)/5) x−y=((21)/5) { ((x=((19)/5))),((y=−(2/5))) :} Second case x−2y=3 and x−3y=5 ⇒y=−2 and x=−1 so x−y=1 { ((x=−1)),((y=−2)) :}

$${x}+\mathrm{2}\mid{y}\mid=\mathrm{3} \\ $$$${First}\:{case}\:\:\:\:{x}+\mathrm{2}{y}=\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}−\mathrm{3}{y}=\mathrm{5}\:\:\:\Rightarrow\mathrm{5}{y}=−\mathrm{2}\:\:\Rightarrow{y}=−\frac{\mathrm{2}}{\mathrm{5}}\:\:\:\:{x}=\frac{\mathrm{19}}{\mathrm{5}} \\ $$$${x}−{y}=\frac{\mathrm{21}}{\mathrm{5}}\:\:\:\:\:\:\begin{cases}{{x}=\frac{\mathrm{19}}{\mathrm{5}}}\\{{y}=−\frac{\mathrm{2}}{\mathrm{5}}}\end{cases} \\ $$$${Second}\:{case} \\ $$$${x}−\mathrm{2}{y}=\mathrm{3}\:\:{and}\:\:\:{x}−\mathrm{3}{y}=\mathrm{5}\:\:\:\Rightarrow{y}=−\mathrm{2}\:\:\:{and}\:\:\:{x}=−\mathrm{1} \\ $$$${so}\:\:\:\:{x}−{y}=\mathrm{1}\:\:\:\begin{cases}{{x}=−\mathrm{1}}\\{{y}=−\mathrm{2}}\end{cases} \\ $$

Answered by mathmax by abdo last updated on 27/Jun/20

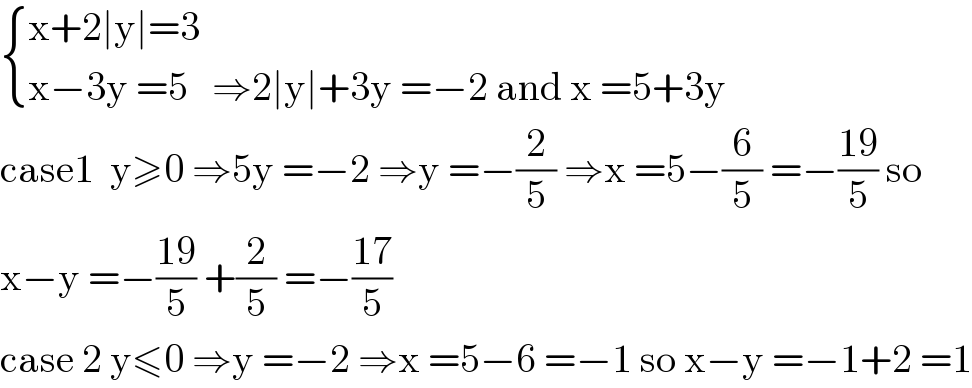
{ ((x+2∣y∣=3)),((x−3y =5 ⇒2∣y∣+3y =−2 and x =5+3y)) :} case1 y≥0 ⇒5y =−2 ⇒y =−(2/5) ⇒x =5−(6/5) =−((19)/5) so x−y =−((19)/5) +(2/5) =−((17)/5) case 2 y≤0 ⇒y =−2 ⇒x =5−6 =−1 so x−y =−1+2 =1

$$\begin{cases}{\mathrm{x}+\mathrm{2}\mid\mathrm{y}\mid=\mathrm{3}}\\{\mathrm{x}−\mathrm{3y}\:=\mathrm{5}\:\:\:\Rightarrow\mathrm{2}\mid\mathrm{y}\mid+\mathrm{3y}\:=−\mathrm{2}\:\mathrm{and}\:\mathrm{x}\:=\mathrm{5}+\mathrm{3y}}\end{cases} \\ $$$$\mathrm{case1}\:\:\mathrm{y}\geqslant\mathrm{0}\:\Rightarrow\mathrm{5y}\:=−\mathrm{2}\:\Rightarrow\mathrm{y}\:=−\frac{\mathrm{2}}{\mathrm{5}}\:\Rightarrow\mathrm{x}\:=\mathrm{5}−\frac{\mathrm{6}}{\mathrm{5}}\:=−\frac{\mathrm{19}}{\mathrm{5}}\:\mathrm{so} \\ $$$$\mathrm{x}−\mathrm{y}\:=−\frac{\mathrm{19}}{\mathrm{5}}\:+\frac{\mathrm{2}}{\mathrm{5}}\:=−\frac{\mathrm{17}}{\mathrm{5}} \\ $$$$\mathrm{case}\:\mathrm{2}\:\mathrm{y}\leqslant\mathrm{0}\:\Rightarrow\mathrm{y}\:=−\mathrm{2}\:\Rightarrow\mathrm{x}\:=\mathrm{5}−\mathrm{6}\:=−\mathrm{1}\:\mathrm{so}\:\mathrm{x}−\mathrm{y}\:=−\mathrm{1}+\mathrm{2}\:=\mathrm{1} \\ $$

Commented by Rasheed.Sindhi last updated on 27/Jun/20

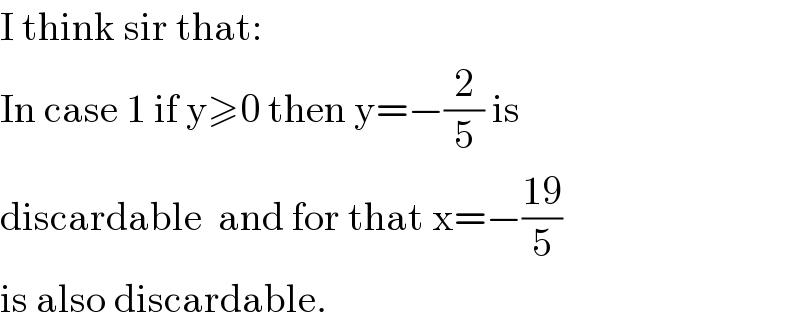
I think sir that: In case 1 if y≥0 then y=−(2/5) is discardable and for that x=−((19)/5) is also discardable.

$$\mathrm{I}\:\mathrm{think}\:\mathrm{sir}\:\mathrm{that}: \\ $$$$\mathrm{In}\:\mathrm{case}\:\mathrm{1}\:\mathrm{if}\:\mathrm{y}\geqslant\mathrm{0}\:\mathrm{then}\:\mathrm{y}=−\frac{\mathrm{2}}{\mathrm{5}}\:\mathrm{is} \\ $$$$\mathrm{discardable}\:\:\mathrm{and}\:\mathrm{for}\:\mathrm{that}\:\mathrm{x}=−\frac{\mathrm{19}}{\mathrm{5}} \\ $$$$\mathrm{is}\:\mathrm{also}\:\mathrm{discardable}. \\ $$

Answered by john santu last updated on 27/Jun/20

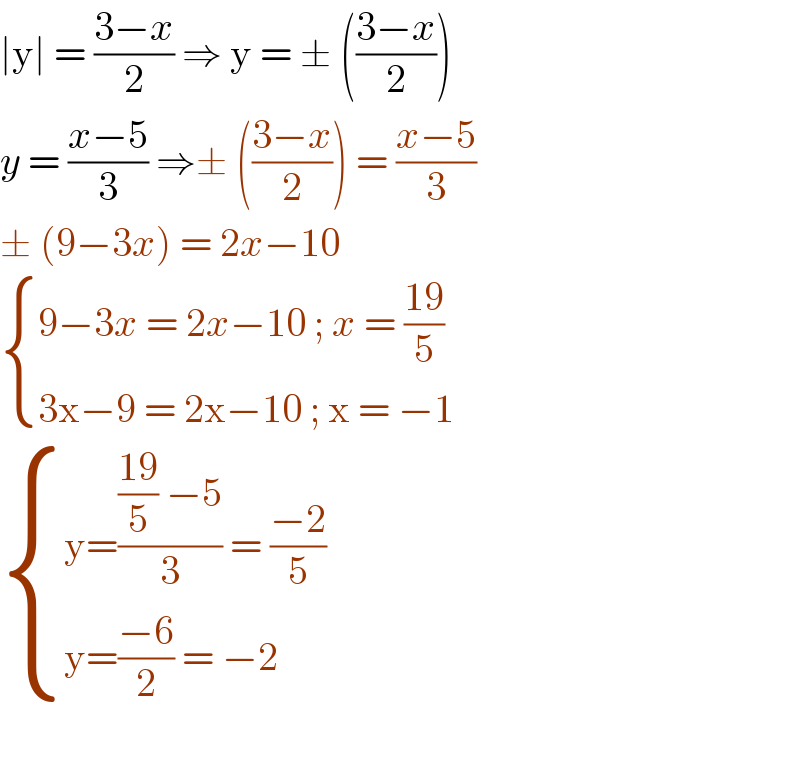
∣y∣ = ((3−x)/2) ⇒ y = ± (((3−x)/2)) y = ((x−5)/3) ⇒± (((3−x)/2)) = ((x−5)/3) ± (9−3x) = 2x−10 { ((9−3x = 2x−10 ; x = ((19)/5))),((3x−9 = 2x−10 ; x = −1 )) :} { ((y=((((19)/5) −5)/3) = ((−2)/5))),((y=((−6)/2) = −2)) :}

$$\mid\mathrm{y}\mid\:=\:\frac{\mathrm{3}−{x}}{\mathrm{2}}\:\Rightarrow\:\mathrm{y}\:=\:\pm\:\left(\frac{\mathrm{3}−{x}}{\mathrm{2}}\right) \\ $$$${y}\:=\:\frac{{x}−\mathrm{5}}{\mathrm{3}}\:\Rightarrow\pm\:\left(\frac{\mathrm{3}−{x}}{\mathrm{2}}\right)\:=\:\frac{{x}−\mathrm{5}}{\mathrm{3}} \\ $$$$\pm\:\left(\mathrm{9}−\mathrm{3}{x}\right)\:=\:\mathrm{2}{x}−\mathrm{10} \\ $$$$\begin{cases}{\mathrm{9}−\mathrm{3}{x}\:=\:\mathrm{2}{x}−\mathrm{10}\:;\:{x}\:=\:\frac{\mathrm{19}}{\mathrm{5}}}\\{\mathrm{3x}−\mathrm{9}\:=\:\mathrm{2x}−\mathrm{10}\:;\:\mathrm{x}\:=\:−\mathrm{1}\:}\end{cases} \\ $$$$\begin{cases}{\mathrm{y}=\frac{\frac{\mathrm{19}}{\mathrm{5}}\:−\mathrm{5}}{\mathrm{3}}\:=\:\frac{−\mathrm{2}}{\mathrm{5}}}\\{\mathrm{y}=\frac{−\mathrm{6}}{\mathrm{2}}\:=\:−\mathrm{2}}\end{cases} \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply