Question Number 100622 by MJS last updated on 27/Jun/20
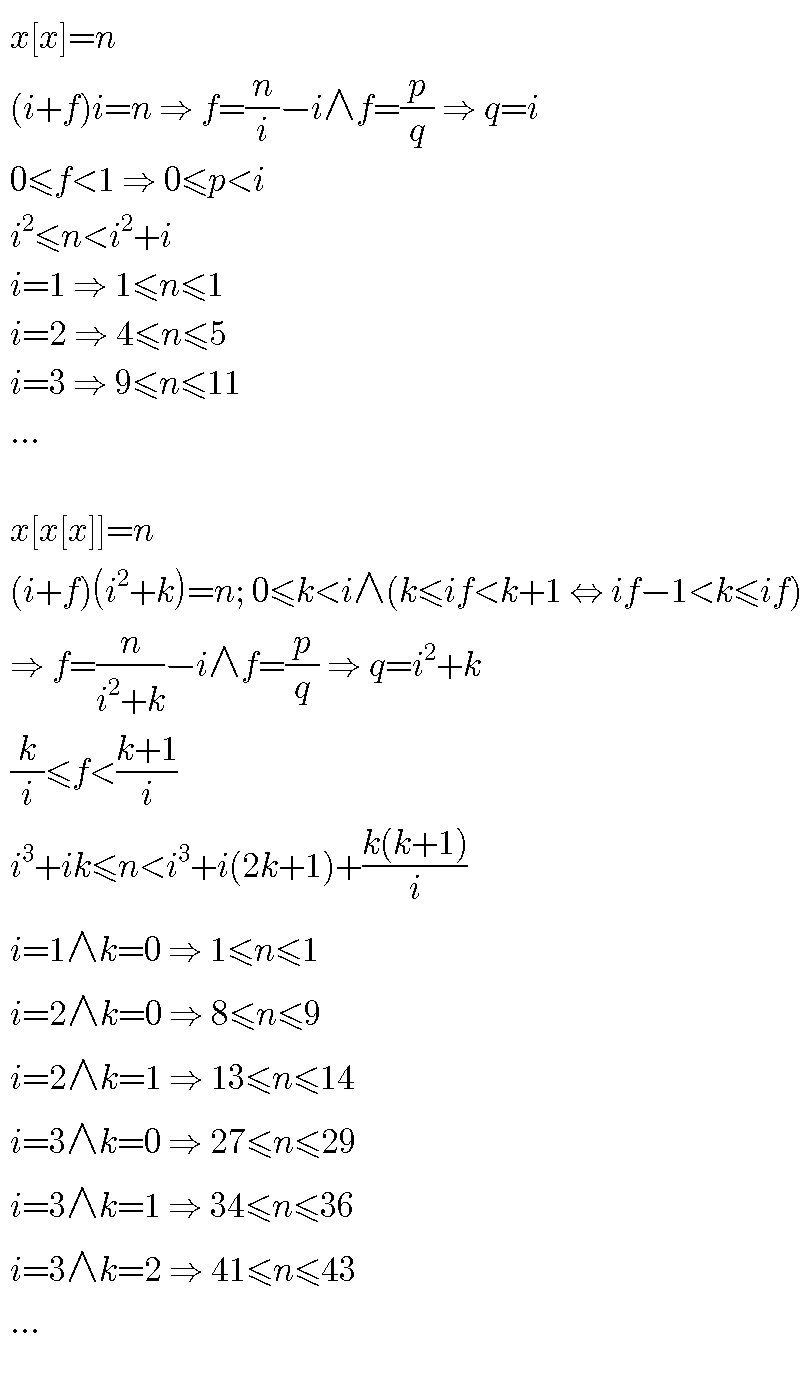
Commented by MJS last updated on 27/Jun/20
![building on my work, can someone try to find the possible values for x∈Q and x[x[x[x]]]=n∈N ? in the picture, i and f are the integer and the fractional part of x](https://www.tinkutara.com/question/Q100623.png)
$$\mathrm{building}\:\mathrm{on}\:\mathrm{my}\:\mathrm{work},\:\mathrm{can}\:\mathrm{someone}\:\mathrm{try}\:\mathrm{to} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{possible}\:\mathrm{values}\:\mathrm{for}\:{x}\in\mathbb{Q}\:\mathrm{and} \\ $$$${x}\left[{x}\left[{x}\left[{x}\right]\right]\right]={n}\in\mathbb{N}\:? \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{picture},\:{i}\:\mathrm{and}\:{f}\:\mathrm{are}\:\mathrm{the}\:\mathrm{integer}\:\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{fractional}\:\mathrm{part}\:\mathrm{of}\:{x} \\ $$
Commented by prakash jain last updated on 03/Jul/20

$$\mathrm{Q96329}\:\mathrm{has}\:\mathrm{a}\:\mathrm{special}\:\mathrm{case}. \\ $$$${x}\lfloor{x}\lfloor{x}\lfloor{x}\rfloor\rfloor\rfloor={n} \\ $$$$\mathrm{Trying}\:\mathrm{for}\:\mathrm{general}\:\mathrm{case} \\ $$$${x}\leqslant\lfloor{n}^{\mathrm{1}/\mathrm{4}} \rfloor \\ $$$${x}={i}+{f}\:\mathrm{where}\:{i}\leqslant\lfloor{n}^{\mathrm{1}/\mathrm{4}} \rfloor \\ $$$${x}\leqslant{n}^{\mathrm{1}/\mathrm{4}} \Rightarrow{x}\lfloor{x}\lfloor{x}\rfloor\rfloor\rfloor\geqslant{n}^{\mathrm{3}/\mathrm{4}} \\ $$$$\mathrm{induction}\:\mathrm{may}\:\mathrm{help}. \\ $$
