Question Number 100653 by Ar Brandon last updated on 28/Jun/20

Answered by mathmax by abdo last updated on 28/Jun/20
![1) f(x) =((sin(nx))/(sinx)) is continue on]0,(π/2)] ⇒ integrable at V(0) we have f(x)∼((nx)/x) =n so I_n exist 2)I_n −I_(n−2) =∫_0 ^(π/2) ((sin(nx)−sin(n−2)x)/(sinx))dx sinp −sinq =sinp +sin(−q) =cos((π/2)−p) +cos((π/2) +q) =2cos(((π−p+q)/2)) cos(((−p−q)/2)) =2cos((π/2)−((p−q)/2))cos(((p+q)/2)) =2cos(((p+q)/2))sin(((p−q)/2)) ⇒sin(nx)−sin(n−2)x =2 cos(((nx+nx−2x)/2))sin(((nx−nx+2x)/2)) =2cos(n−1)x sinx ⇒I_n −I_(n−2) =2∫_0 ^(π/2) cos(n−1)x dx =2[(1/(n−1))sin(n−1)x]_0 ^(π/2) =(2/(n−1))sin(n−1)(π/2) =(2/(n−1)) sin(((nπ)/2)−(π/2)) =−(2/(n−1))cos(((nπ)/2)) (n≥2) ⇒I_2 −I_0 =−(2/1)cos(π) =2 but I_0 =0 ⇒I_2 =2 3)we have I_n −I_(n−2) =−(2/(n−1)) cos(((nπ)/2)) ⇒I_(2n) −I_(2n−2) =−((2(−1)^n )/(n−1)) ⇒ Σ_(k=2) ^n (I_(2k) −I_(2k−2) ) =2 Σ_(k=2) ^n (((−1)^(k−1) )/(k−1)) ⇒ I_4 −I_2 +I_6 −I_4 +....I_(2n) −I_(2n−2) =2 Σ_(k=2) ^n (((−1)^(k−1) )/(k−1)) ⇒ I_(2n) =I_2 +2Σ_(k=2) ^n (((−1)^(k−1) )/(k−1)) =2 +2Σ_(k=1) ^(n−1) (((−1)^k )/k) I_(2n+1) −I_(2n−1) =−(2/(2n)) cos((((2n+1)π)/2)) =−(1/n)cos(nπ +(π/2)) =0 ⇒ I_(2n+1) =I_(2n−1) =I_1 =(π/2)](https://www.tinkutara.com/question/Q100662.png)
$$\left.\mathrm{1}\left.\right)\left.\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{sin}\left(\mathrm{nx}\right)}{\mathrm{sinx}}\:\mathrm{is}\:\mathrm{continue}\:\:\mathrm{on}\right]\mathrm{0},\frac{\pi}{\mathrm{2}}\right]\:\Rightarrow\:\mathrm{integrable}\:\mathrm{at}\:\mathrm{V}\left(\mathrm{0}\right)\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\sim\frac{\mathrm{nx}}{\mathrm{x}}\:=\mathrm{n}\:\mathrm{so}\:\:\mathrm{I}_{\mathrm{n}} \mathrm{exist} \\ $$$$\left.\mathrm{2}\right)\mathrm{I}_{\mathrm{n}} \:−\mathrm{I}_{\mathrm{n}−\mathrm{2}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{sin}\left(\mathrm{nx}\right)−\mathrm{sin}\left(\mathrm{n}−\mathrm{2}\right)\mathrm{x}}{\mathrm{sinx}}\mathrm{dx} \\ $$$$\mathrm{sinp}\:−\mathrm{sinq}\:=\mathrm{sinp}\:+\mathrm{sin}\left(−\mathrm{q}\right)\:=\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{p}\right)\:+\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}\:+\mathrm{q}\right) \\ $$$$=\mathrm{2cos}\left(\frac{\pi−\mathrm{p}+\mathrm{q}}{\mathrm{2}}\right)\:\mathrm{cos}\left(\frac{−\mathrm{p}−\mathrm{q}}{\mathrm{2}}\right)\:=\mathrm{2cos}\left(\frac{\pi}{\mathrm{2}}−\frac{\mathrm{p}−\mathrm{q}}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\mathrm{p}+\mathrm{q}}{\mathrm{2}}\right) \\ $$$$=\mathrm{2cos}\left(\frac{\mathrm{p}+\mathrm{q}}{\mathrm{2}}\right)\mathrm{sin}\left(\frac{\mathrm{p}−\mathrm{q}}{\mathrm{2}}\right)\:\Rightarrow\mathrm{sin}\left(\mathrm{nx}\right)−\mathrm{sin}\left(\mathrm{n}−\mathrm{2}\right)\mathrm{x}\:=\mathrm{2}\:\mathrm{cos}\left(\frac{\mathrm{nx}+\mathrm{nx}−\mathrm{2x}}{\mathrm{2}}\right)\mathrm{sin}\left(\frac{\mathrm{nx}−\mathrm{nx}+\mathrm{2x}}{\mathrm{2}}\right) \\ $$$$=\mathrm{2cos}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}\:\mathrm{sinx}\:\Rightarrow\mathrm{I}_{\mathrm{n}} −\mathrm{I}_{\mathrm{n}−\mathrm{2}} =\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}\:\mathrm{dx} \\ $$$$=\mathrm{2}\left[\frac{\mathrm{1}}{\mathrm{n}−\mathrm{1}}\mathrm{sin}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{\mathrm{2}}{\mathrm{n}−\mathrm{1}}\mathrm{sin}\left(\mathrm{n}−\mathrm{1}\right)\frac{\pi}{\mathrm{2}}\:=\frac{\mathrm{2}}{\mathrm{n}−\mathrm{1}}\:\mathrm{sin}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{2}}\right) \\ $$$$=−\frac{\mathrm{2}}{\mathrm{n}−\mathrm{1}}\mathrm{cos}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)\:\:\:\left(\mathrm{n}\geqslant\mathrm{2}\right)\:\Rightarrow\mathrm{I}_{\mathrm{2}} −\mathrm{I}_{\mathrm{0}} =−\frac{\mathrm{2}}{\mathrm{1}}\mathrm{cos}\left(\pi\right)\:=\mathrm{2}\:\mathrm{but}\:\mathrm{I}_{\mathrm{0}} =\mathrm{0}\:\Rightarrow\mathrm{I}_{\mathrm{2}} =\mathrm{2} \\ $$$$\left.\mathrm{3}\right)\mathrm{we}\:\mathrm{have}\:\mathrm{I}_{\mathrm{n}} −\mathrm{I}_{\mathrm{n}−\mathrm{2}} =−\frac{\mathrm{2}}{\mathrm{n}−\mathrm{1}}\:\mathrm{cos}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)\:\Rightarrow\mathrm{I}_{\mathrm{2n}} −\mathrm{I}_{\mathrm{2n}−\mathrm{2}} =−\frac{\mathrm{2}\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}−\mathrm{1}}\:\Rightarrow \\ $$$$\sum_{\mathrm{k}=\mathrm{2}} ^{\mathrm{n}} \:\left(\mathrm{I}_{\mathrm{2k}} −\mathrm{I}_{\mathrm{2k}−\mathrm{2}} \right)\:=\mathrm{2}\:\sum_{\mathrm{k}=\mathrm{2}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} }{\mathrm{k}−\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{I}_{\mathrm{4}} \:−\mathrm{I}_{\mathrm{2}} \:+\mathrm{I}_{\mathrm{6}} −\mathrm{I}_{\mathrm{4}} \:+….\mathrm{I}_{\mathrm{2n}} \:−\mathrm{I}_{\mathrm{2n}−\mathrm{2}} =\mathrm{2}\:\sum_{\mathrm{k}=\mathrm{2}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} }{\mathrm{k}−\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{I}_{\mathrm{2n}} =\mathrm{I}_{\mathrm{2}} \:+\mathrm{2}\sum_{\mathrm{k}=\mathrm{2}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} }{\mathrm{k}−\mathrm{1}}\:=\mathrm{2}\:+\mathrm{2}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{k}}\: \\ $$$$\mathrm{I}_{\mathrm{2n}+\mathrm{1}} −\mathrm{I}_{\mathrm{2n}−\mathrm{1}} =−\frac{\mathrm{2}}{\mathrm{2n}}\:\mathrm{cos}\left(\frac{\left(\mathrm{2n}+\mathrm{1}\right)\pi}{\mathrm{2}}\right)\:=−\frac{\mathrm{1}}{\mathrm{n}}\mathrm{cos}\left(\mathrm{n}\pi\:+\frac{\pi}{\mathrm{2}}\right)\:=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{I}_{\mathrm{2n}+\mathrm{1}} =\mathrm{I}_{\mathrm{2n}−\mathrm{1}} \:=\mathrm{I}_{\mathrm{1}} =\frac{\pi}{\mathrm{2}} \\ $$
Commented by mathmax by abdo last updated on 28/Jun/20
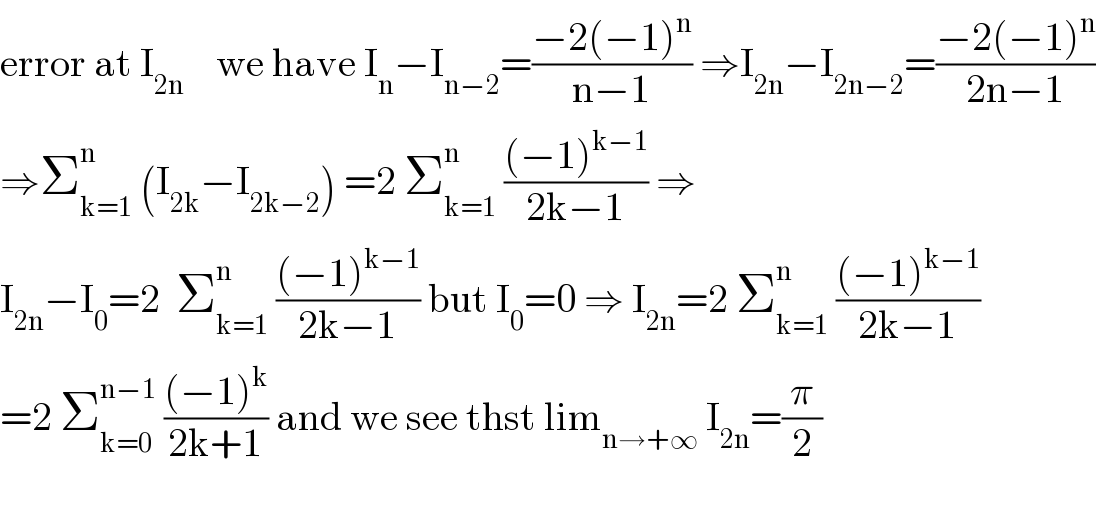
$$\mathrm{error}\:\mathrm{at}\:\mathrm{I}_{\mathrm{2n}} \:\:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{I}_{\mathrm{n}} −\mathrm{I}_{\mathrm{n}−\mathrm{2}} =\frac{−\mathrm{2}\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}−\mathrm{1}}\:\Rightarrow\mathrm{I}_{\mathrm{2n}} −\mathrm{I}_{\mathrm{2n}−\mathrm{2}} =\frac{−\mathrm{2}\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}−\mathrm{1}} \\ $$$$\Rightarrow\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\left(\mathrm{I}_{\mathrm{2k}} −\mathrm{I}_{\mathrm{2k}−\mathrm{2}} \right)\:=\mathrm{2}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} }{\mathrm{2k}−\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{I}_{\mathrm{2n}} −\mathrm{I}_{\mathrm{0}} =\mathrm{2}\:\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} }{\mathrm{2k}−\mathrm{1}}\:\mathrm{but}\:\mathrm{I}_{\mathrm{0}} =\mathrm{0}\:\Rightarrow\:\mathrm{I}_{\mathrm{2n}} =\mathrm{2}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} }{\mathrm{2k}−\mathrm{1}} \\ $$$$=\mathrm{2}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{2k}+\mathrm{1}}\:\mathrm{and}\:\mathrm{we}\:\mathrm{see}\:\mathrm{thst}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{I}_{\mathrm{2n}} =\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 28/Jun/20
Thank you Sir ��
