Question-100695

Question Number 100695 by john santu last updated on 28/Jun/20

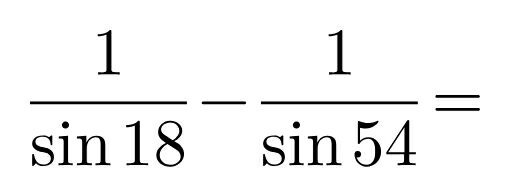
Commented by bobhans last updated on 28/Jun/20

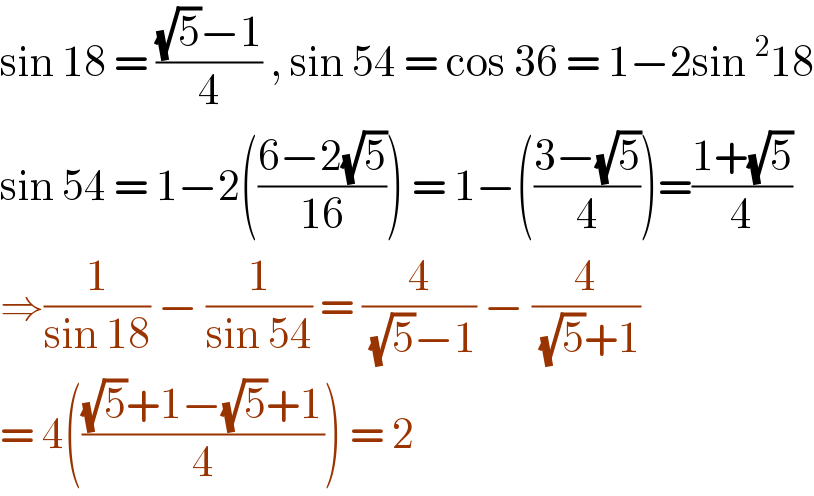
sin 18 = (((√5)−1)/4) , sin 54 = cos 36 = 1−2sin^2 18 sin 54 = 1−2(((6−2(√5))/(16))) = 1−(((3−(√5))/4))=((1+(√5))/4) ⇒(1/(sin 18)) − (1/(sin 54)) = (4/( (√5)−1)) − (4/( (√5)+1)) = 4((((√5)+1−(√5)+1)/4)) = 2

$$\mathrm{sin}\:\mathrm{18}\:=\:\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\:,\:\mathrm{sin}\:\mathrm{54}\:=\:\mathrm{cos}\:\mathrm{36}\:=\:\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{18} \\ $$$$\mathrm{sin}\:\mathrm{54}\:=\:\mathrm{1}−\mathrm{2}\left(\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}}\right)\:=\:\mathrm{1}−\left(\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{4}}\right)=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{18}}\:−\:\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{54}}\:=\:\frac{\mathrm{4}}{\:\sqrt{\mathrm{5}}−\mathrm{1}}\:−\:\frac{\mathrm{4}}{\:\sqrt{\mathrm{5}}+\mathrm{1}} \\ $$$$=\:\mathrm{4}\left(\frac{\sqrt{\mathrm{5}}+\mathrm{1}−\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}\right)\:=\:\mathrm{2} \\ $$

Commented by john santu last updated on 28/Jun/20

$$\mathrm{correct}\:\mathrm{sir}\:\mathrm{bob} \\ $$

Commented by Dwaipayan Shikari last updated on 28/Jun/20

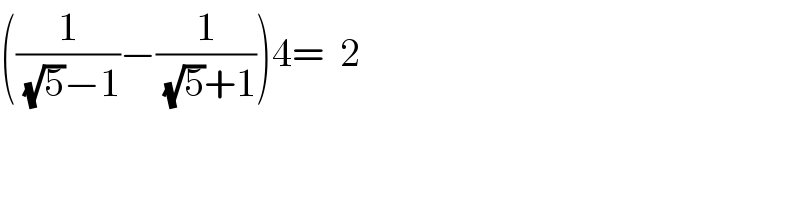
$$\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}−\mathrm{1}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}+\mathrm{1}}\right)\mathrm{4}=\:\:\mathrm{2} \\ $$

Answered by EquationMaker2305 last updated on 28/Jun/20

$$\mathrm{0}.\mathrm{45800357} \\ $$

Commented by prakash jain last updated on 28/Jun/20

You seem to have calculated this value using a calculator in radian mode. Change mode ro degrees and you will get correct answer.

$$\mathrm{You}\:\mathrm{seem}\:\mathrm{to}\:\mathrm{have}\:\mathrm{calculated}\:\mathrm{this} \\ $$$$\mathrm{value}\:\mathrm{using}\:\mathrm{a}\:\mathrm{calculator}\:\mathrm{in}\:\mathrm{radian} \\ $$$$\mathrm{mode}.\:\mathrm{Change}\:\mathrm{mode}\:\mathrm{ro}\:\mathrm{degrees} \\ $$$$\mathrm{and}\:\mathrm{you}\:\mathrm{will}\:\mathrm{get}\:\mathrm{correct}\:\mathrm{answer}. \\ $$

Commented by EquationMaker2305 last updated on 28/Jun/20

Please post plain text comments instead, it much readable.

Answered by 1549442205 last updated on 28/Jun/20

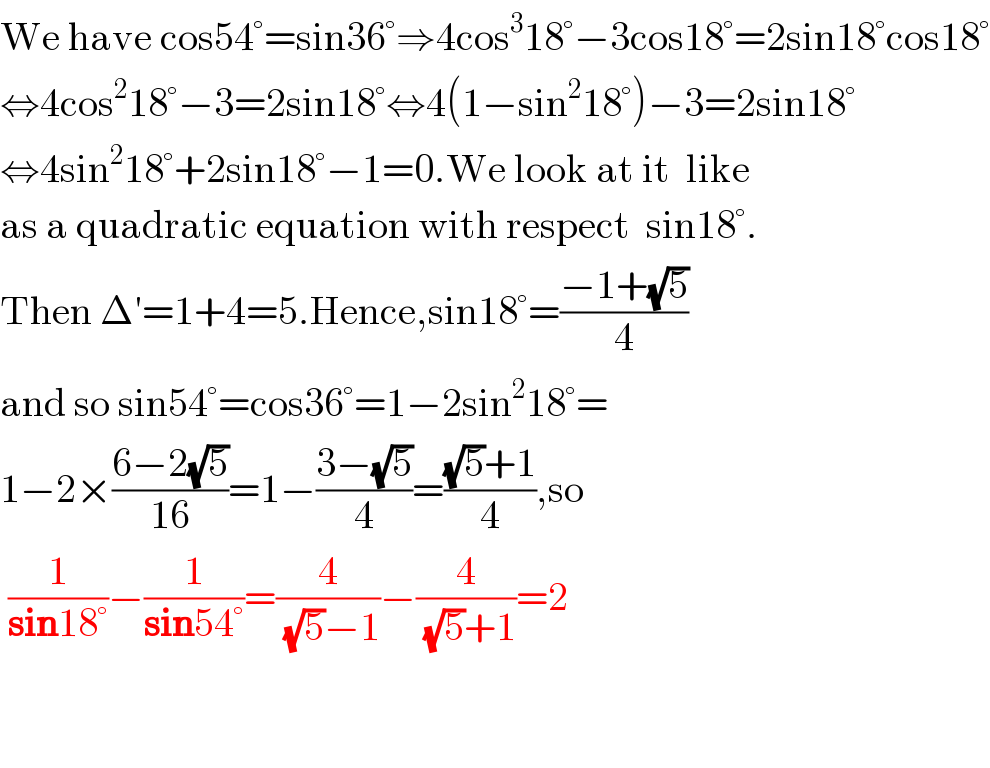
We have cos54°=sin36°⇒4cos^3 18°−3cos18°=2sin18°cos18° ⇔4cos^2 18°−3=2sin18°⇔4(1−sin^2 18°)−3=2sin18° ⇔4sin^2 18°+2sin18°−1=0.We look at it like as a quadratic equation with respect sin18°. Then Δ′=1+4=5.Hence,sin18°=((−1+(√5))/4) and so sin54°=cos36°=1−2sin^2 18°= 1−2×((6−2(√5))/(16))=1−((3−(√5))/4)=(((√5)+1)/4),so (1/(sin18°))−(1/(sin54°))=(4/( (√5)−1))−(4/( (√5)+1))=2

$$\mathrm{We}\:\mathrm{have}\:\mathrm{cos54}°=\mathrm{sin36}°\Rightarrow\mathrm{4cos}^{\mathrm{3}} \mathrm{18}°−\mathrm{3cos18}°=\mathrm{2sin18}°\mathrm{cos18}° \\ $$$$\Leftrightarrow\mathrm{4cos}^{\mathrm{2}} \mathrm{18}°−\mathrm{3}=\mathrm{2sin18}°\Leftrightarrow\mathrm{4}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{18}°\right)−\mathrm{3}=\mathrm{2sin18}° \\ $$$$\Leftrightarrow\mathrm{4sin}^{\mathrm{2}} \mathrm{18}°+\mathrm{2sin18}°−\mathrm{1}=\mathrm{0}.\mathrm{We}\:\mathrm{look}\:\mathrm{at}\:\mathrm{it}\:\:\mathrm{like} \\ $$$$\mathrm{as}\:\mathrm{a}\:\mathrm{quadratic}\:\mathrm{equation}\:\mathrm{with}\:\mathrm{respect}\:\:\mathrm{sin18}°. \\ $$$$\mathrm{Then}\:\Delta'=\mathrm{1}+\mathrm{4}=\mathrm{5}.\mathrm{Hence},\mathrm{sin18}°=\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\mathrm{and}\:\mathrm{so}\:\mathrm{sin54}°=\mathrm{cos36}°=\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \mathrm{18}°= \\ $$$$\mathrm{1}−\mathrm{2}×\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}}=\mathrm{1}−\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{4}}=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}},\mathrm{so} \\ $$$$\:\frac{\mathrm{1}}{\boldsymbol{\mathrm{sin}}\mathrm{18}°}−\frac{\mathrm{1}}{\boldsymbol{\mathrm{sin}}\mathrm{54}°}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{5}}−\mathrm{1}}−\frac{\mathrm{4}}{\:\sqrt{\mathrm{5}}+\mathrm{1}}=\mathrm{2} \\ $$$$ \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply