Question Number 100789 by 175 last updated on 28/Jun/20

Answered by maths mind last updated on 28/Jun/20
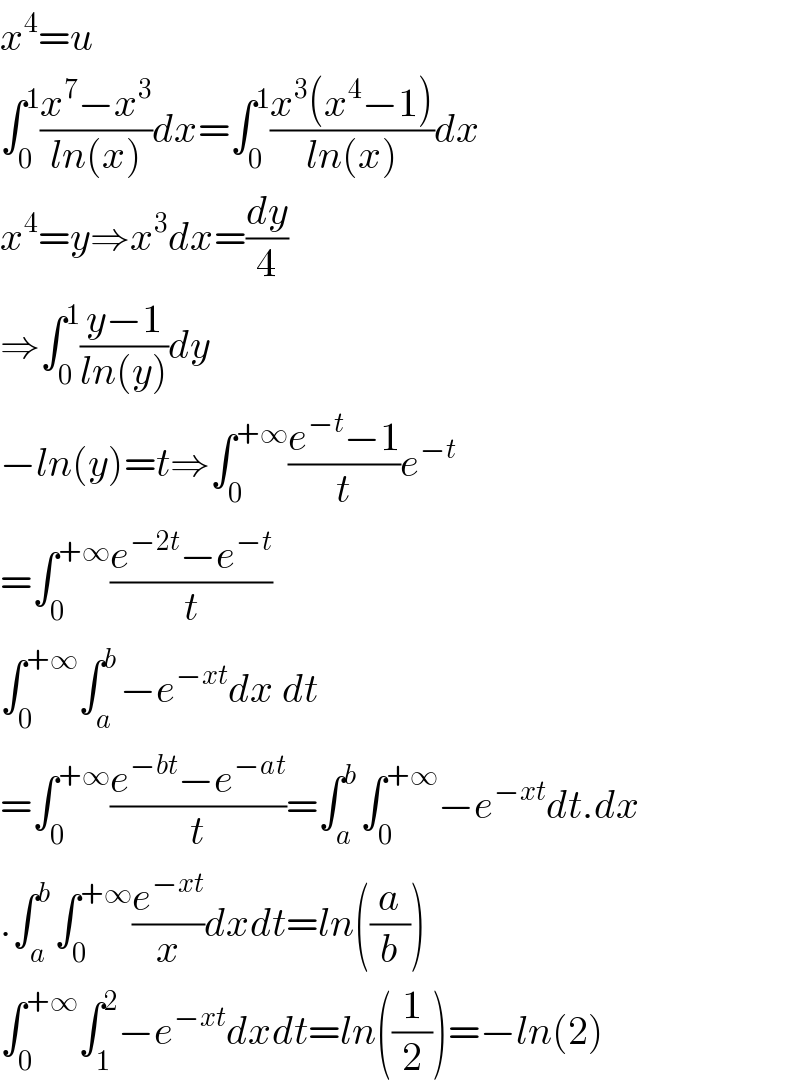
$${x}^{\mathrm{4}} ={u} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{7}} −{x}^{\mathrm{3}} }{{ln}\left({x}\right)}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{3}} \left({x}^{\mathrm{4}} −\mathrm{1}\right)}{{ln}\left({x}\right)}{dx} \\ $$$${x}^{\mathrm{4}} ={y}\Rightarrow{x}^{\mathrm{3}} {dx}=\frac{{dy}}{\mathrm{4}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{y}−\mathrm{1}}{{ln}\left({y}\right)}{dy} \\ $$$$−{ln}\left({y}\right)={t}\Rightarrow\int_{\mathrm{0}} ^{+\infty} \frac{{e}^{−{t}} −\mathrm{1}}{{t}}{e}^{−{t}} \\ $$$$=\int_{\mathrm{0}} ^{+\infty} \frac{{e}^{−\mathrm{2}{t}} −{e}^{−{t}} }{{t}} \\ $$$$\int_{\mathrm{0}} ^{+\infty} \int_{{a}} ^{{b}} −{e}^{−{xt}} {dx}\:{dt} \\ $$$$=\int_{\mathrm{0}} ^{+\infty} \frac{{e}^{−{bt}} −{e}^{−{at}} }{{t}}=\int_{{a}} ^{{b}} \int_{\mathrm{0}} ^{+\infty} −{e}^{−{xt}} {dt}.{dx} \\ $$$$.\int_{{a}} ^{{b}} \int_{\mathrm{0}} ^{+\infty} \frac{{e}^{−{xt}} }{{x}}{dxdt}={ln}\left(\frac{{a}}{{b}}\right) \\ $$$$\int_{\mathrm{0}} ^{+\infty} \int_{\mathrm{1}} ^{\mathrm{2}} −{e}^{−{xt}} {dxdt}={ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=−{ln}\left(\mathrm{2}\right) \\ $$
Commented by Ar Brandon last updated on 28/Jun/20
Hello Sir, I really admire the technics which you apply when solving maths questions especially when it concerns CALCULUS. Can you please recommend me any textbook amongst those which helped you improve your skills ? Any language. ��
Commented by maths mind last updated on 28/Jun/20

$${hello}\:{sir}\:{thank}\:{you} \\ $$$${i}\:{didnt}\:{use}\:{realy}\:{used}\:{a}\:{book}\:{only}\:{som}\:{lesson}\:{in}\:{my}\:{sgudy} \\ $$$${i}\:{used}\:{books}\:{i}\mathrm{7}\:{topologie}\:{and}\:{algebraic}\:{geometry} \\ $$$${one}\:{Book}\:{that}\:{i}\:{find}\:{good}\:{realy}\:{chalanging}\:{problems} \\ $$$$<{impossible}\:{integral}\:{and}\:{sum}> \\ $$
Commented by Ar Brandon last updated on 28/Jun/20
Thanks for your feedback. I'm currently using some JEE textbooks on CALCULUS, and I hope I'll step up.��
Answered by abdomathmax last updated on 28/Jun/20
![I =∫_0 ^1 ((x^7 −x^3 )/(lnx))dx changement lnx =−t give I =−∫_0 ^(+∞ ) ((e^(−7t) −e^(−3t) )/(−t))(−e^(−t) )dt =−∫_0 ^∞ ((e^(−8t) −e^(−4t) )/t) dt let f(a) =∫_0 ^∞ ((e^(−8t) −e^(−4t) )/t) e^(−at) dt (a>0) we have f^′ (a) =−∫_0 ^∞ (e^(−8t) −e^(−4t) )e^(−at) dt =∫_0 ^∞ (e^(−(a+4)t) −e^(−(a+8)t) )dt =[−(1/((a+4)))e^((a+4)t) +(1/(a+8)) e^(−(a+8)t) ]_0 ^(+∞) =(1/(a+4))−(1/(a+8)) ⇒f(a) =ln(((a+4)/(a+8))) +c(c=lim_(a→+∞) f(a)=0 ⇒f(a) =ln(((a+4)/(a+8)))f(0) =ln((1/2))=∫_0 ^∞ ((e^(−8t) −e^(−4t) )/t)dt ⇒ I =−f(0) =ln2](https://www.tinkutara.com/question/Q100824.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{7}} −\mathrm{x}^{\mathrm{3}} }{\mathrm{lnx}}\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{lnx}\:=−\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{I}\:=−\int_{\mathrm{0}} ^{+\infty\:} \:\frac{\mathrm{e}^{−\mathrm{7t}} −\mathrm{e}^{−\mathrm{3t}} }{−\mathrm{t}}\left(−\mathrm{e}^{−\mathrm{t}} \right)\mathrm{dt} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\mathrm{8t}} −\mathrm{e}^{−\mathrm{4t}} }{\mathrm{t}}\:\mathrm{dt}\:\:\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{8t}} −\mathrm{e}^{−\mathrm{4t}} }{\mathrm{t}}\:\mathrm{e}^{−\mathrm{at}} \mathrm{dt} \\ $$$$\left(\mathrm{a}>\mathrm{0}\right)\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}^{'} \left(\mathrm{a}\right)\:=−\int_{\mathrm{0}} ^{\infty} \left(\mathrm{e}^{−\mathrm{8t}} −\mathrm{e}^{−\mathrm{4t}} \right)\mathrm{e}^{−\mathrm{at}} \:\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\mathrm{e}^{−\left(\mathrm{a}+\mathrm{4}\right)\mathrm{t}} −\mathrm{e}^{−\left(\mathrm{a}+\mathrm{8}\right)\mathrm{t}} \right)\mathrm{dt} \\ $$$$=\left[−\frac{\mathrm{1}}{\left(\mathrm{a}+\mathrm{4}\right)}\mathrm{e}^{\left(\boldsymbol{\mathrm{a}}+\mathrm{4}\right)\boldsymbol{\mathrm{t}}} \:+\frac{\mathrm{1}}{\boldsymbol{\mathrm{a}}+\mathrm{8}}\:\boldsymbol{\mathrm{e}}^{−\left(\boldsymbol{\mathrm{a}}+\mathrm{8}\right)\boldsymbol{\mathrm{t}}} \right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{a}+\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{a}+\mathrm{8}}\:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)\:=\mathrm{ln}\left(\frac{\mathrm{a}+\mathrm{4}}{\mathrm{a}+\mathrm{8}}\right)\:+\mathrm{c}\left(\mathrm{c}=\mathrm{lim}_{\mathrm{a}\rightarrow+\infty} \mathrm{f}\left(\mathrm{a}\right)=\mathrm{0}\right. \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{a}\right)\:=\mathrm{ln}\left(\frac{\mathrm{a}+\mathrm{4}}{\mathrm{a}+\mathrm{8}}\right)\mathrm{f}\left(\mathrm{0}\right)\:=\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{8t}} −\mathrm{e}^{−\mathrm{4t}} }{\mathrm{t}}\mathrm{dt}\:\:\Rightarrow \\ $$$$\mathrm{I}\:=−\mathrm{f}\left(\mathrm{0}\right)\:=\mathrm{ln2} \\ $$$$ \\ $$
