Menu Close

Question-100806

Tinku Tara 0 Comments
Pin




Question Number 100806 by I want to learn more last updated on 28/Jun/20
Commented by I want to learn more last updated on 28/Jun/20
33 sir.
$$\mathrm{33}\:\:\mathrm{sir}. \\ $$
Commented by john santu last updated on 28/Jun/20
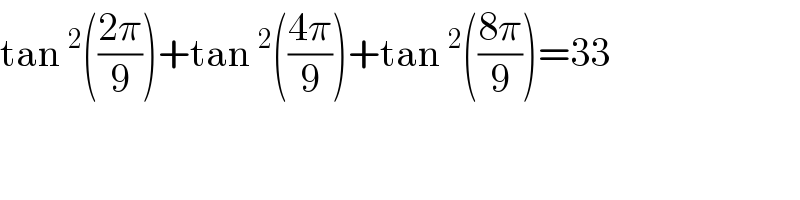
tan^2 (((2π)/9))+tan^2 (((4π)/9))+tan^2 (((8π)/9))=33
$$\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\mathrm{2}\pi}{\mathrm{9}}\right)+\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\mathrm{4}\pi}{\mathrm{9}}\right)+\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\mathrm{8}\pi}{\mathrm{9}}\right)=\mathrm{33} \\ $$
Commented by I want to learn more last updated on 28/Jun/20
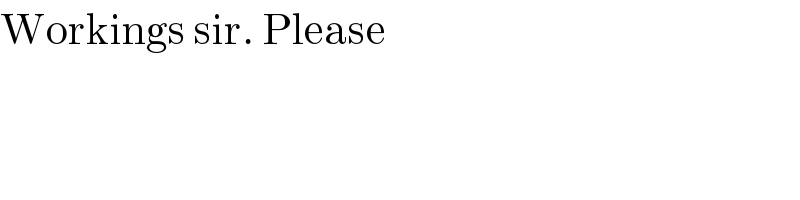
Workings sir. Please
$$\mathrm{Workings}\:\mathrm{sir}.\:\mathrm{Please} \\ $$
Answered by MJS last updated on 28/Jun/20
put tan^2 x =t ⇒ t+((4t)/((t−1)^2 ))+((16t(t−1)^2 )/((t^2 −6t+1)^2 ))=33 ⇒ t^7 −47t^6 +545t^5 −2291t^4 +3611t^3 −2205t^2 +483t−33=0 (t^4 −14t^3 +56t^2 −62t+11)(t^3 −33t^2 +27t−3)=0 now solve this approximately or exactly, for the first factor the exact solution is not useable. for 0≤x<(π/3) it leads to { ((x_1 =π/9)),((x_2 =2π/9)),((x_3 =4π/9)) :} from the 3^(rd) −degree−polynome { ((x_4 ≈.436880)),((x_5 ≈.873645)),((x_6 ≈1.13059)),((x_7 ≈1.22795)) :} from tbe 4^(th) −degree−polynome the solutions of the given equation are x_i +2nπ and (2n+1)π−x_i with 1≤i≤7 and n∈Z
$$\mathrm{put}\:\mathrm{tan}^{\mathrm{2}} \:{x}\:={t} \\ $$$$\Rightarrow \\ $$$${t}+\frac{\mathrm{4}{t}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{16}{t}\left({t}−\mathrm{1}\right)^{\mathrm{2}} }{\left({t}^{\mathrm{2}} −\mathrm{6}{t}+\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{33} \\ $$$$\Rightarrow \\ $$$${t}^{\mathrm{7}} −\mathrm{47}{t}^{\mathrm{6}} +\mathrm{545}{t}^{\mathrm{5}} −\mathrm{2291}{t}^{\mathrm{4}} +\mathrm{3611}{t}^{\mathrm{3}} −\mathrm{2205}{t}^{\mathrm{2}} +\mathrm{483}{t}−\mathrm{33}=\mathrm{0} \\ $$$$\left({t}^{\mathrm{4}} −\mathrm{14}{t}^{\mathrm{3}} +\mathrm{56}{t}^{\mathrm{2}} −\mathrm{62}{t}+\mathrm{11}\right)\left({t}^{\mathrm{3}} −\mathrm{33}{t}^{\mathrm{2}} +\mathrm{27}{t}−\mathrm{3}\right)=\mathrm{0} \\ $$$$\mathrm{now}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{approximately}\:\mathrm{or}\:\mathrm{exactly}, \\ $$$$\mathrm{for}\:\mathrm{the}\:\mathrm{first}\:\mathrm{factor}\:\mathrm{the}\:\mathrm{exact}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{not} \\ $$$$\mathrm{useable}. \\ $$$$\mathrm{for}\:\mathrm{0}\leqslant{x}<\frac{\pi}{\mathrm{3}}\:\mathrm{it}\:\mathrm{leads}\:\mathrm{to} \\ $$$$\begin{cases}{{x}_{\mathrm{1}} =\pi/\mathrm{9}}\\{{x}_{\mathrm{2}} =\mathrm{2}\pi/\mathrm{9}}\\{{x}_{\mathrm{3}} =\mathrm{4}\pi/\mathrm{9}}\end{cases}\:\mathrm{from}\:\mathrm{the}\:\mathrm{3}^{\mathrm{rd}} −\mathrm{degree}−\mathrm{polynome} \\ $$$$\begin{cases}{{x}_{\mathrm{4}} \approx.\mathrm{436880}}\\{{x}_{\mathrm{5}} \approx.\mathrm{873645}}\\{{x}_{\mathrm{6}} \approx\mathrm{1}.\mathrm{13059}}\\{{x}_{\mathrm{7}} \approx\mathrm{1}.\mathrm{22795}}\end{cases}\:\mathrm{from}\:\mathrm{tbe}\:\mathrm{4}^{\mathrm{th}} −\mathrm{degree}−\mathrm{polynome} \\ $$$$\mathrm{the}\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation}\:\mathrm{are} \\ $$$${x}_{{i}} +\mathrm{2}{n}\pi\:\mathrm{and}\:\left(\mathrm{2}{n}+\mathrm{1}\right)\pi−{x}_{{i}} \:\mathrm{with}\:\mathrm{1}\leqslant{i}\leqslant\mathrm{7}\:\mathrm{and}\:{n}\in\mathbb{Z} \\ $$
Commented by maths mind last updated on 28/Jun/20
nice worck sir
$${nice}\:{worck}\:{sir} \\ $$
Commented by I want to learn more last updated on 28/Jun/20
Thanks sir
$$\mathrm{Thanks}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *